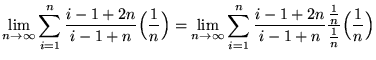
SOLUTION 11 : First algebraically manipulate the expression in order to make a choice for the sampling points. Thus,
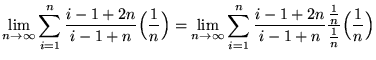
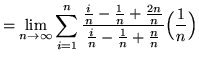
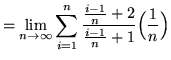 .
.
Choose the sampling point ![]() to be
to be
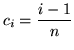
for
![]() . Then
. Then ![]() represents the left-hand endpoints of
represents the left-hand endpoints of ![]() equal-sized subdivisions of the interval
equal-sized subdivisions of the interval ![]() and
and
![]()
for
![]() . Thus,
. Thus,
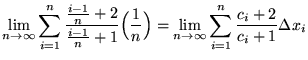
(Let
![]() .)
.)
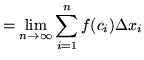
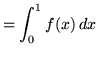
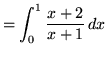 .
.
Click HERE to return to the list of problems.
SOLUTION 12 : First algebraically manipulate the expression in order to make a choice for the sampling points. Thus,
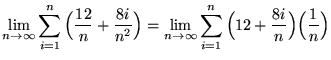 .
.
Choose the sampling point ![]() to be
to be
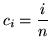
for
![]() . (Note that other choices for
. (Note that other choices for ![]() also lead to correct answers. For example,
also lead to correct answers. For example,
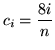 or
or
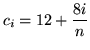 also works. Each choice determines a different interval and a different function !) Then
also works. Each choice determines a different interval and a different function !) Then ![]() represents the right-hand endpoints of
represents the right-hand endpoints of ![]() equal-sized subdivisions of the interval
equal-sized subdivisions of the interval ![]() and
and
![]()
for
![]() . Thus,
. Thus,
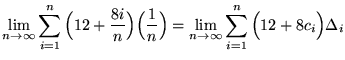
(Let
![]() .)
.)
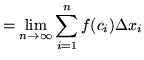
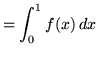
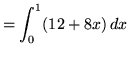 .
.
Click HERE to return to the list of problems.
SOLUTION 13 : First algebraically manipulate the expression in order to make a choice for the sampling points. Thus,
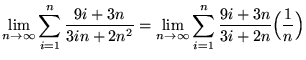
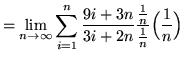
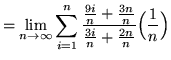
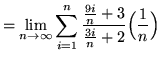 .
.
Choose the sampling point ![]() to be
to be
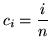
for
![]() . (Note that other choices for
. (Note that other choices for ![]() also lead to correct answers. For example,
also lead to correct answers. For example,
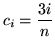 ,
,
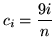 ,
,
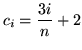 or
or
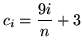 also works. Each choice determines a different interval and a different function !) Then
also works. Each choice determines a different interval and a different function !) Then ![]() represents the right-hand endpoints of
represents the right-hand endpoints of ![]() equal-sized subdivisions of the interval
equal-sized subdivisions of the interval ![]() and
and
![]()
for
![]() . Thus,
. Thus,
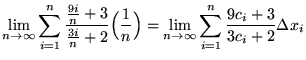
(Let
![]() .)
.)
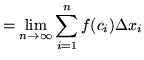
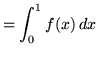
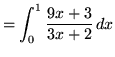 .
.
Click HERE to return to the list of problems.
SOLUTION 14 : Use the limit definition of definite integral to evaluate
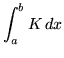 , where
, where ![]() is a constant. Use an arbitrary partition
is a constant. Use an arbitrary partition
![]() and arbitrary sampling numbers
and arbitrary sampling numbers ![]() for
for
![]() . Let
. Let
![]()
and recall that
![]()
and the mesh of the partition is
![]()
for
![]() .
Thus, the definite integral of
.
Thus, the definite integral of ![]() on the interval
on the interval ![]() is defined to be
is defined to be
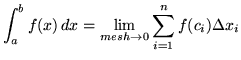
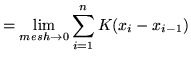
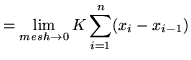
![]()
(This is a telescoping sum.)
![]()
![]()
![]() .
.
Click HERE to return to the list of problems.
SOLUTION 15 : Use the limit definition of definite integral to evaluate
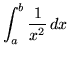 . Use an arbitrary partition
. Use an arbitrary partition
![]() and the sampling number
and the sampling number
![]() for
for
![]() . Begin by showing that
. Begin by showing that
![]() for
for
![]() . Assume that
. Assume that ![]() . Note that
. Note that
![]()
since
![]() , so that
, so that
![]()
or
![]() .
.
Similarly,
![]()
since
![]() , so that
, so that
![]()
or
![]() .
.
This proves that
![]() for
for
![]() .
Let
.
Let
![]()
and recall that
![]()
for
![]() and the mesh of the partition is
and the mesh of the partition is
![]() .
.
Thus, the definite integral of ![]() on the interval
on the interval ![]() is defined to be
is defined to be
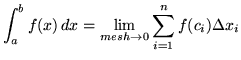
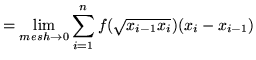
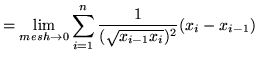
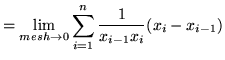
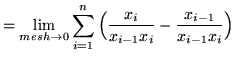
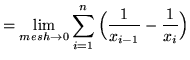
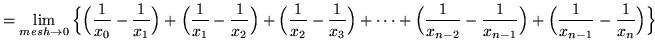
(This is a telescoping sum.)
![]()
![]()
![]() .
.
Click HERE to return to the list of problems.