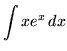 . Let
. Let
![]() and
and
![]()
so that
![]() and
and ![]() .
.
Therefore,
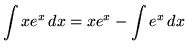
![]() .
.
Click HERE to return to the list of problems.
SOLUTION 2 : Integrate
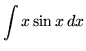 . Let
. Let
![]() and
and
![]()
so that
![]() and
and
![]() .
.
Therefore,
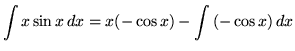
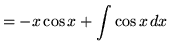
![]() .
.
Click HERE to return to the list of problems.
SOLUTION 3 : Integrate
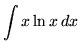 . Let
. Let
![]() and
and
![]()
so that
![]() and
and
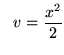 .
.
Therefore,
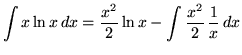
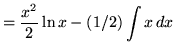
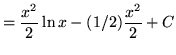
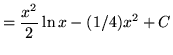 .
.
Click HERE to return to the list of problems.
SOLUTION 4 : Integrate
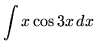 . Let
. Let
![]() and
and
![]()
so that
![]() and
and
![]() .
.
Therefore,
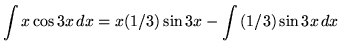
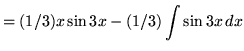
![]()
![]() .
.
Click HERE to return to the list of problems.
SOLUTION 5 : Integrate
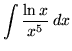 . Let
. Let
![]() and
and
![]()
so that
![]() and
and
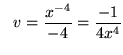 .
.
Therefore,
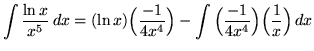
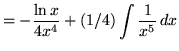
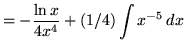
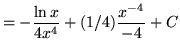
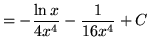 .
.
Click HERE to return to the list of problems.
SOLUTION 6 : Integrate
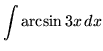 . Let
. Let
![]() and
and
![]()
so that (Don't forget to use the chain rule when differentiating ![]() .)
.)
![]() and
and ![]() .
.
Therefore,
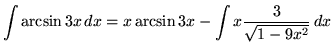
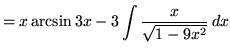 .
.
Now use u-substitution. Let
![]()
so that
![]() ,
,
or
![]() .
.
Then
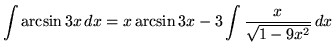
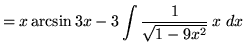
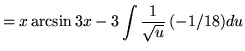
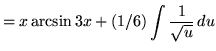
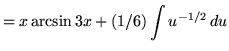
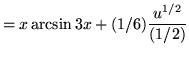 + C
+ C
![]() + C
+ C
![]() + C .
+ C .
Click HERE to return to the list of problems.
SOLUTION 7 : Integrate
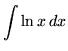 . Let
. Let
![]() and
and
![]()
so that
![]() and
and ![]() .
.
Therefore,
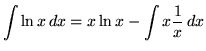
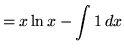
![]() .
.
Click HERE to return to the list of problems.
SOLUTION 8 : Integrate
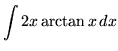 . Let
. Let
![]() and
and
![]()
so that
![]() and
and ![]() .
.
Therefore,
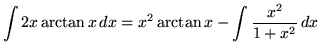
(Add
![]() in the numerator. This will replicate the denominator and allow us to split the function into two parts.)
in the numerator. This will replicate the denominator and allow us to split the function into two parts.)
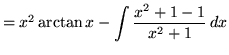
(Please note that there is a TYPO in the next step. The second "-" sign should be a "+" sign. However, subsequent steps are correct.)
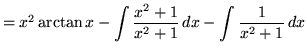
(The remaining steps are all correct.)
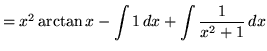
![]() .
.
Click HERE to return to the list of problems.
SOLUTION 9 : Integrate
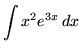 . Let
. Let
![]() and
and
![]()
so that
![]() and
and
![]() .
.
Therefore,
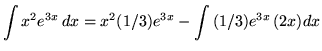
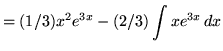 .
.
Integrate by parts again. Let
![]() and
and
![]()
so that
![]() and
and
![]() .
.
Hence,
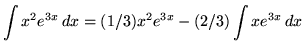
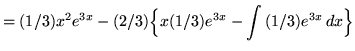
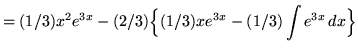
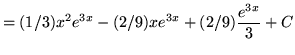
![]() .
.
Click HERE to return to the list of problems.