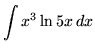 . Let
. Let
![]() and
and
![]()
so that
![]() and
and
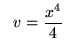 .
.
Therefore,
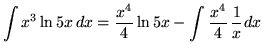
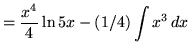
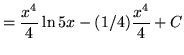
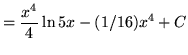 .
.
Click HERE to return to the list of problems.
SOLUTION 11 : Integrate
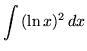 . Let
. Let
![]() and
and
![]()
so that
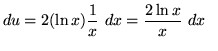 and
and ![]() .
.
Therefore,
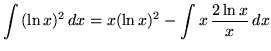
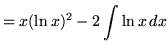 .
.
Use integration by parts again. Let
![]() and
and
![]()
so that
![]() and
and ![]() .
.
Hence,
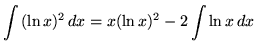
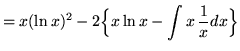
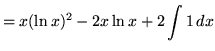
![]() .
.
Click HERE to return to the list of problems.
SOLUTION 12 : Integrate
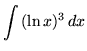 . Let
. Let
ein
![]() and
and
![]()
so that
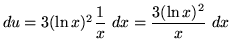 and
and ![]() .
.
Therefore,
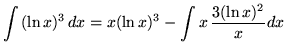
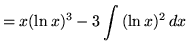 .
.
Use integration by parts again. Let
![]() and
and
![]()
so that
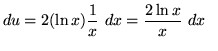 and
and ![]() .
.
Therefore,
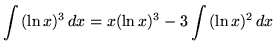
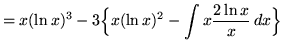
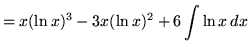 .
.
Use integration by parts for a third time. Let
![]() and
and
![]()
so that
![]() and
and ![]() .
.
Hence,
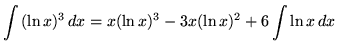
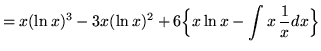
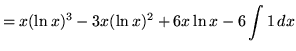
![]() .
.
Click HERE to return to the list of problems.
SOLUTION 13 : Integrate
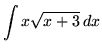 . Let
. Let
![]() and
and
![]()
so that
![]() and
and
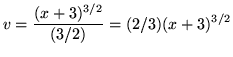 .
.
Therefore,
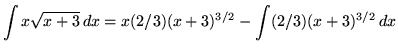
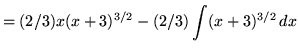
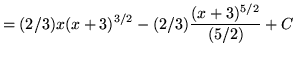
![]() .
.
Click HERE to return to the list of problems.
SOLUTION 14 : Integrate
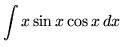 . Let
. Let
![]() and
and
![]()
so that
![]() and
and
![]() .
.
Therefore,
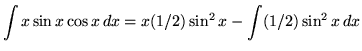
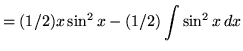 .
.
Now use the trig identity
![]() ,
,
getting
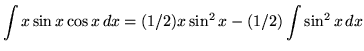
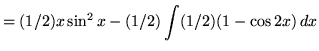
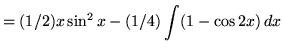
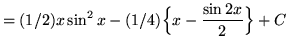
![]() .
.
Click HERE to return to the list of problems.
SOLUTION 15 : Integrate
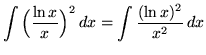 . Let
. Let
![]() and
and
![]()
so that
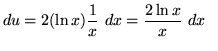 and
and
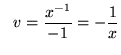 .
.
Therefore,
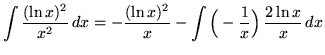
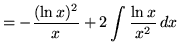 .
.
Use integration by parts again. Let
![]() and
and
![]()
so that
![]() and
and
![]() .
.
Hence
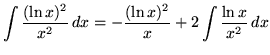
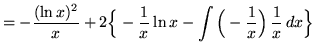
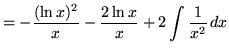
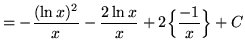
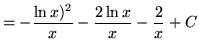 .
.
Click HERE to return to the list of problems.