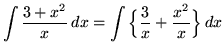
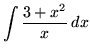Next: About this document ...



SOLUTION 1 : Integrate $ \displaystyle{ \int { 3+x^2 \over x } \,dx } $ . First, split this rational function into two parts. Thus,

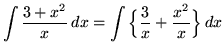
$ \displaystyle{ \int { 3+x^2 \over x } \,dx } = \displaystyle{ \int \Big\{ { 3 \over x } + { x^2 \over x } \Big\} \,dx } $

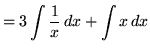
$ = \displaystyle{ 3\int { 1 \over x }\,dx } + \displaystyle{ \int x \,dx } $

(Now use formula 1 from the introduction to this section, and note that 3C is replaced with C since C is an arbitrary constant.)

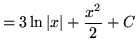$ = \displaystyle{ 3 \ln \vert x\vert + { x^2 \over 2 } + C } $ .

Click HERE to return to the list of problems.




SOLUTION 2 : Integrate 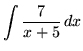$ \displaystyle{ \int { 7 \over x+5 } \,dx } $ . Use u-substitution. Let

$ u = x+5 $

so that

$ du = (1) dx = dx $ .

Substitute into the original problem, replacing all forms of $ x $, getting

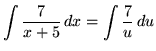
$ \displaystyle{ \int { 7 \over x+5 } \,dx } = \displaystyle{ \int { 7 \over u } \,du } $

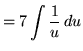
$ = \displaystyle{ 7 \int { 1 \over u } \,du } $

(Now use formula 1 from the introduction to this section, and note that 7C is replaced with C since C is an arbitrary constant.)

$ = 7 \ln \vert u\vert + C $

$ = 7 \ln \vert x+5\vert + C $ .

Click HERE to return to the list of problems.




SOLUTION 3 : Integrate 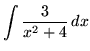$ \displaystyle{ \int { 3 \over x^2+4 } \,dx } $ . Rewrite the function and use formula 3 from the introduction to this section. Then

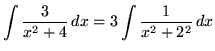
$ \displaystyle{ \int { 3 \over x^2+4 } \,dx } = \displaystyle{ 3 \int { 1 \over x^2+2^2 } \,dx } $

(Note that 3C is replaced with C since C is an arbitrary constant.)

$ = 3 (1/2) \arctan(x/2) + C $

$ = (3/2) \arctan(x/2) + C $ .

Click HERE to return to the list of problems.




SOLUTION 4 : Integrate 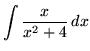$ \displaystyle{ \int { x \over x^2+4 } \,dx } $ . Use u-substitution. Let

$ u = x^2+4 $

so that

$ du = 2x dx $ ,

or

$ (1/2) du = x dx $ .

Substitute into the original problem, replacing all forms of $ x $, getting

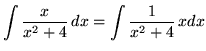
$ \displaystyle{ \int { x \over x^2+4 } \,dx } = \displaystyle{ \int { 1 \over x^2+4 } \, xdx } $

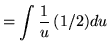
$ = \displaystyle{ \int { 1 \over u } \, (1/2)du } $

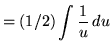
$ = \displaystyle{ (1/2) \int { 1 \over u } \, du } $

(Now use formula 1 from the introduction to this section, and note that (1/2)C is replaced with C since C is an arbitrary constant.)

$ = (1/2) \displaystyle{ \ln \vert u\vert + C } $

$ = (1/2) \displaystyle{ \ln \vert x^2+4\vert + C } $ .

Click HERE to return to the list of problems.




SOLUTION 5 : Integrate 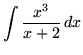$ \displaystyle{ \int { x^3 \over x+2 } \,dx } $ . First, use polynomial division to divide $ x^3 $ by $ x+2 $ . The result is

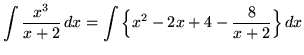
$ \displaystyle{ \int { x^3 \over x+2 } \,dx } = \displaystyle{ \int \Big\{ x^2-2x+4-{8 \over x+2 } \Big\} \,dx } $

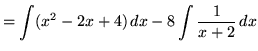$ = \displaystyle{ \int (x^2-2x+4) \,dx } - \displaystyle{ 8 \int {1 \over x+2 } \,dx } $ .

In the second integral, use u-substitution. Let

$ u = x+2 $

so that

$ du = (1) dx = dx $ .

Substitute into the original problem, replacing all forms of $ x $, getting

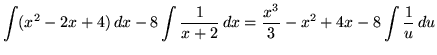
$ \displaystyle{ \int (x^2-2x+4) \,dx } - \displaystyle{ 8 \int {1 \over x+2 } ... ...aystyle{ { x^3 \over 3 }-x^2+4x } - \displaystyle{ 8 \int {1 \over u } \,du } $

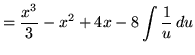
$ = \displaystyle{ { x^3 \over 3 }-x^2+4x } - \displaystyle{ 8 \int {1 \over u } \,du } $

(Now use formula 1 from the introduction to this section, and note that (-8)C is replaced with C since C is an arbitrary constant.)

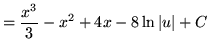
$ = \displaystyle{ { x^3 \over 3 }-x^2+4x } - 8 \ln \vert u\vert + C $

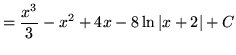$ = \displaystyle{ { x^3 \over 3 }-x^2+4x } - 8 \ln \vert x+2\vert + C $ .

Click HERE to return to the list of problems.




SOLUTION 6 : Integrate 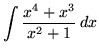$ \displaystyle{ \int { x^4+x^3 \over x^2+1 } \,dx } $. First, use polynomial division to divide $ x^4+x^3 $ by $ x^2+1 $ . The result is

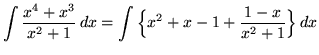
$ \displaystyle{ \int { x^4+x^3 \over x^2+1 } \,dx } = \displaystyle{ \int \Big\{ x^2+x-1+{1-x \over x^2+1 } \Big\} \,dx } $

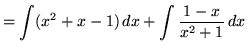
$ = \displaystyle{ \int (x^2+x-1) \,dx } + \displaystyle{ \int {1-x \over x^2+1 } \,dx } $

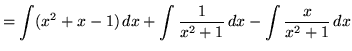$ = \displaystyle{ \int (x^2+x-1) \,dx } + \displaystyle{ \int {1 \over x^2+1 } \,dx } - \displaystyle{ \int {x \over x^2+1 } \,dx }$ .

In the third integral, use u-substitution. Let

$ u = x^2+1 $

so that

$ du = 2x dx $ ,

or

$ (1/2) du = x dx $ .

For the second integral, use formula 2 from the introduction to this section. In the third integral substitute into the original problem, replacing all forms of $ x $, getting

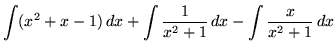
$ \displaystyle{ \int (x^2+x-1) \,dx } + \displaystyle{ \int {1 \over x^2+1 } \,dx } - \displaystyle{ \int {x \over x^2+1 } \,dx } $

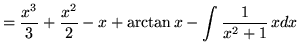
$ = \displaystyle{ {x^3 \over 3}+ {x^2 \over 2}-x } + \displaystyle{ \arctan x } - \displaystyle{ \int {1 \over x^2+1 } \,xdx }$

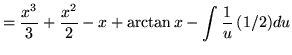
$ = \displaystyle{ {x^3 \over 3}+ {x^2 \over 2}-x } + \displaystyle{ \arctan x } - \displaystyle{ \int {1 \over u } \,(1/2)du }$

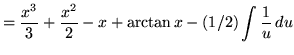
$ = \displaystyle{ {x^3 \over 3}+ {x^2 \over 2}-x } + \displaystyle{ \arctan x } - \displaystyle{ (1/2)\int {1 \over u } \,du }$

(Now use formula 1 from the introduction to this section, and note that (-1/2)C is replaced with C since C is an arbitrary constant.)

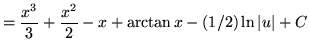
$ = \displaystyle{ {x^3 \over 3}+ {x^2 \over 2}-x } + \displaystyle{ \arctan x } - \displaystyle{ (1/2)\ln \vert u\vert } + C $

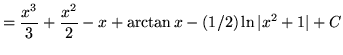$ = \displaystyle{ {x^3 \over 3}+ {x^2 \over 2}-x } + \displaystyle{ \arctan x } - \displaystyle{ (1/2)\ln \vert x^2+1\vert } + C $ .

Click HERE to return to the list of problems.




SOLUTION 7 : Integrate 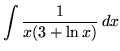$ \displaystyle{ \int { 1 \over x (3+ \ln x ) } \,dx } $. Use u-substitution. Let

$ u = 3+ \ln x $

so that

$ du = \displaystyle{ 1 \over x } dx $ .

Substitute into the original problem, replacing all forms of $ x $, getting

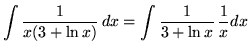
$ \displaystyle{ \int { 1 \over x (3+ \ln x ) } \,dx } = \displaystyle{ \int { 1 \over 3+ \ln x } \,{ 1 \over x} dx } $

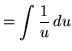
$ = \displaystyle{ \int { 1 \over u } \, du } $

(Use formula 1 from the introduction to this section.)

$ = \displaystyle{ \ln \vert u\vert } + C $

$ = \displaystyle{ \ln \vert 3+ \ln x\vert } + C $ .

Click HERE to return to the list of problems.




SOLUTION 8 : Integrate 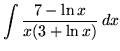$ \displaystyle{ \int { 7 - \ln x \over x (3+ \ln x) } \,dx } $ . Use u-substitution. Let

$ u = 3+ \ln x $

so that

$ du = \displaystyle{ 1 \over x } dx $ .

In addition, we can "back substitute" with

$ \ln x = u-3 $ .

Substitute into the original problem, replacing all forms of $ x $, getting

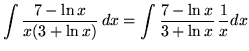
$ \displaystyle{ \int { 7 - \ln x \over x (3+ \ln x) } \,dx } = \displaystyle{ \int { 7 - \ln x \over 3+ \ln x } \, {1 \over x} dx } $

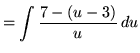
$ = \displaystyle{ \int { 7 - (u-3) \over u } \, du } $

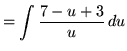
$ = \displaystyle{ \int { 7-u+3 \over u } \, du } $

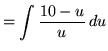
$ = \displaystyle{ \int { 10-u \over u } \, du } $

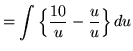
$ = \displaystyle{ \int \Big\{ { 10 \over u } - { u \over u } \Big\} \, du } $

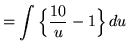
$ = \displaystyle{ \int \Big\{ { 10 \over u } - 1 \Big\} \, du } $

$ = \displaystyle{ 10 \ln \vert u\vert - u } + C $

$ = \displaystyle{ 10 \ln \vert 3+ \ln x\vert - (3 + \ln x) } + C $

$ = \displaystyle{ 10 \ln \vert 3+ \ln x\vert - 3 - \ln x } + C $

(Combine $ -3 $ and $ C $ since $ C $ is an arbitrary constant.)

$ = \displaystyle{ 10 \ln \vert 3+ \ln x\vert - \ln x } + C $ .

Click HERE to return to the list of problems.






Next: About this document ...
Duane Kouba 2000-04-12