Solutions to Integration Using a Power Substitution

SOLUTIONS TO INTEGRATION USING A POWER SUBSTITUTION

SOLUTION 7 : Integrate $\displaystyle{ \int { \sqrt{x} + 1 \over \sqrt{x} ( \sqrt[3] {x} + 1 ) } \, dx }$ . Because we want to simultaneously eliminate a square root and a cube root, use the power substitution

so that

$u = x^{1/6}$ ,

$\sqrt{x} = x^{1/2} = (u^6)^{1/2} = u^3$ ,

$\sqrt[3] {x} = x^{1/3} = (u^6)^{1/3} = u^2$ ,

and

Substitute into the original problem, replacing all forms of , getting

$\displaystyle{ \int { \sqrt{x} + 1 \over \sqrt{x} ( \sqrt[3] {x} + 1 ) } \, dx } = \displaystyle{ \int { u^3 + 1 \over u^3(u^2+1) } \, (6u^5) du }$

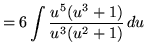
$= \displaystyle{ 6 \int { u^5(u^3+1) \over u^3(u^2+1) } \, du }$

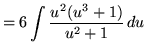
$= \displaystyle{ 6 \int { u^2(u^3+1) \over u^2+1 } \, du }$

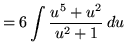
$= \displaystyle{ 6 \int { u^5+u^2 \over u^2+1 } \, du }$

(Use polynomial division. PLEASE INSERT A FACTOR OF 6 WHICH WAS ACCIDENTLY LEFT OUT.)

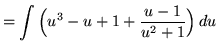
$= \displaystyle{ \int \Big( u^3-u+1+ {u-1 \over u^2+1 } \Big) \, du }$

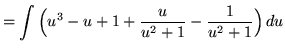
$= \displaystyle{ \int \Big( u^3-u+1+ {u \over u^2+1} - {1 \over u^2+1} \Big) \, du }$

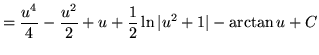
$= \displaystyle{ {u^4 \over 4} - {u^2 \over 2} + u + {1 \over 2} \ln \vert u^2+1\vert - \arctan u } + C$

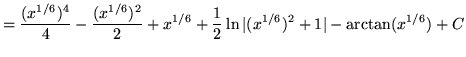
$= \displaystyle{ {(x^{1/6})^4 \over 4} - {(x^{1/6})^2 \over 2} + x^{1/6} + {1 \over 2} \ln \vert(x^{1/6})^2+1\vert - \arctan (x^{1/6}) } + C$

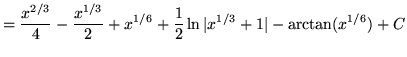$= \displaystyle{ {x^{2/3} \over 4} - {x^{1/3} \over 2} + x^{1/6} + {1 \over 2} \ln \vert x^{1/3}+1\vert - \arctan (x^{1/6}) } + C$ .

Click HERE to return to the list of problems.

SOLUTION 8 : Integrate 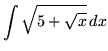$\displaystyle{ \int \sqrt{ 5 + \sqrt{x} } \, dx }$ . Remove the ``outside" square root first. Use the power substitution

$5 + \sqrt{x} = u^2$

so that

$u = \sqrt{ 5 + \sqrt{x} }$ ,

$\sqrt{x} = u^2-5$ ,

and (Use the chain rule.)

Substitute into the original problem, replacing all forms of , getting

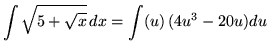
$\displaystyle{ \int \sqrt{ 5 + \sqrt{x} } \, dx } = \displaystyle{ \int (u) \, (4u^3-20u) du }$

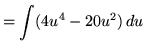
$= \displaystyle{ \int (4u^4-20u^2) \, du }$

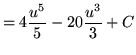
$= \displaystyle{ 4{u^5 \over 5}-20{u^3 \over 3} } + C$

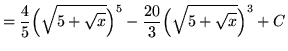
$= \displaystyle{ {4 \over 5}\Big(\sqrt{ 5 + \sqrt{x} }\Big)^5 - {20 \over 3}\Big(\sqrt{ 5 + \sqrt{x} }\Big)^3 } + C$

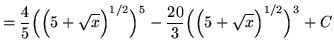
$= \displaystyle{ {4 \over 5}\Big(\Big( 5 + \sqrt{x} \Big)^{1/2}\Big)^5 - {20 \over 3}\Big(\Big( 5 + \sqrt{x} \Big)^{1/2} \Big)^3 } + C$

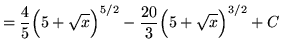$= \displaystyle{ {4 \over 5}\Big(5 + \sqrt{x}\Big)^{5/2} - {20 \over 3}\Big(5 + \sqrt{x} \Big)^{3/2} } + C$ .

Click HERE to return to the list of problems.

SOLUTION 9 : Integrate $\displaystyle{ \int \sqrt[3] { 1 + \sqrt{x-3} } \, dx }$ . Remove the cube root first. Use the power substitution

$1 + \sqrt{x-3} = u^3$

so that

$u = \sqrt[3] { 1 + \sqrt{x-3} }$ ,

$\sqrt{x-3} = u^3-1$ ,

and (Use the chain rule.)

Substitute into the original problem, replacing all forms of , getting

$\displaystyle{ \int \sqrt[3] { 1 + \sqrt{x-3} } \, dx } = \displaystyle{ \int (u) \, (6u^5-6u^2) du }$

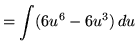
$= \displaystyle{ \int (6u^6-6u^3) \, du }$

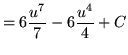
$= \displaystyle{ 6{u^7 \over 7} - 6{u^4 \over 4} } + C$

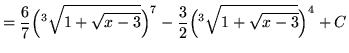
$= \displaystyle{ {6 \over 7}\Big({^3}\sqrt{ 1 + \sqrt{x-3} }\Big)^7 - {3 \over 2}\Big({^3}\sqrt{ 1 + \sqrt{x-3} }\Big)^4 } + C$

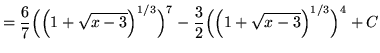
$= \displaystyle{ {6 \over 7}\Big( \Big( 1 + \sqrt{x-3} \Big)^{1/3} \Big)^7 - {3 \over 2}\Big( \Big( 1 + \sqrt{x-3} \Big)^{1/3} \Big)^4 } + C$

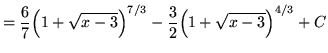$= \displaystyle{ {6 \over 7}\Big(1 + \sqrt{x-3}\Big)^{7/3} - {3 \over 2}\Big(1 + \sqrt{x-3} \Big)^{4/3} } + C$ .

Click HERE to return to the list of problems.

SOLUTION 10 : Integrate 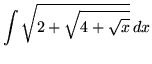$\displaystyle{ \int \sqrt{ 2 + \sqrt{ 4 + \sqrt{x} } } \, dx }$ . Remove the ``outside" square root first. Use the power substitution

$2 + \sqrt{ 4 + \sqrt{x} } = u^2$

so that

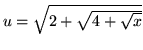
$u = \sqrt{ 2 + \sqrt{ 4 + \sqrt{x} } }$

$\longrightarrow \sqrt{ 4 + \sqrt{x} } = u^2-2$

$\longrightarrow \sqrt{x} = (u^2-2)^2-4$

$\longrightarrow x = ((u^2-2)^2-4)^2$ ,

and (Use the chain rule.)

Substitute into the original problem, replacing all forms of , getting

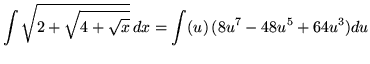
$\displaystyle{ \int \sqrt{ 2 + \sqrt{ 4 + \sqrt{x} } } \, dx } = \displaystyle{ \int (u) \, (8u^7-48u^5+64u^3) du }$

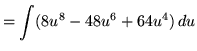
$= \displaystyle{ \int (8u^8-48u^6+64u^4) \, du }$

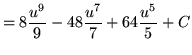
$= \displaystyle{ 8{u^9 \over 9} - 48{u^7 \over 7} + 64{u^5 \over 5} } + C$

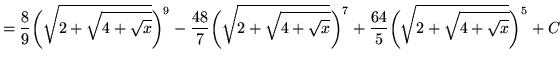
$= \displaystyle{ {8 \over 9}\bigg(\sqrt{ 2 + \sqrt{ 4 + \sqrt{x} } }\bigg)^9 -... ...}\bigg)^7 + {64 \over 5}\bigg(\sqrt{ 2 + \sqrt{ 4 + \sqrt{x} } }\bigg)^5 } + C$

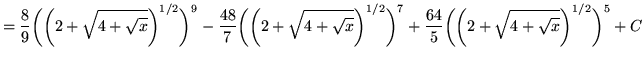
$= \displaystyle{ {8 \over 9}\bigg(\bigg( 2 + \sqrt{ 4 + \sqrt{x} } \bigg)^{1/2... ... {64 \over 5}\bigg(\bigg( 2 + \sqrt{ 4 + \sqrt{x} } \bigg)^{1/2}\bigg)^5 } + C$

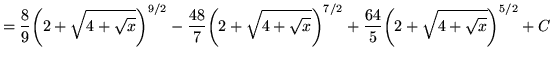$= \displaystyle{ {8 \over 9}\bigg( 2 + \sqrt{ 4 + \sqrt{x} } \bigg)^{9/2} - {4... ...\bigg)^{7/2} + {64 \over 5}\bigg( 2 + \sqrt{ 4 + \sqrt{x} } \bigg)^{5/2} } + C$ .

Click HERE to return to the list of problems.

About this document ...

Duane Kouba 2000-05-09