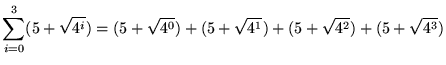
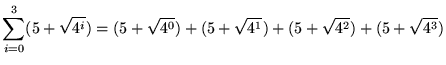
![]()
= (5+1) + (5+2) + (5+4) + (5+8)
= 6 + 7 + 9 + 13
= 35 .
Click HERE to return to the list of problems.
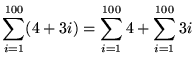
(The above step is nothing more than changing the order and grouping of the original summation.)
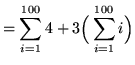
(Placing 3 in front of the second summation is simply factoring 3 from each term in the summation. Now apply Rule 1 to the first summation and Rule 2 to the second summation.)
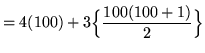
= 400 + 15,150
= 15,550 .
Click HERE to return to the list of problems.
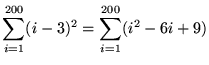
(Separate this summation into three separate summations.)
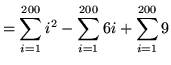
(Factor out the number 6 in the second summation.)
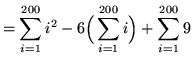
(Apply Rules 1, 2, and 3.)
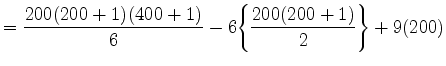
= 2,686,700 - 120,600 + 1800
= 2,567,900 .
Click HERE to return to the list of problems.
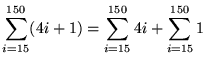
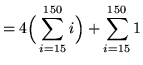
(Since each summation begins with i=15, WE CANNOT USE THE RULES IN THE FORM THAT THEY ARE GIVEN. Observe the following simple method to correct this shortcoming.)
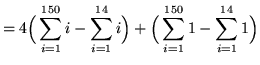
(Now apply Rules 1 and 2.)
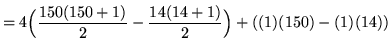
= 4(11,325 - 105) + (136)
= 45,016 .
Click HERE to return to the list of problems.
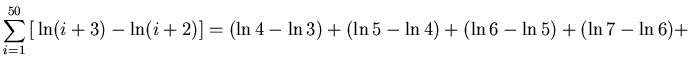
![]()
(Note that ![]() cancels, then
cancels, then ![]() ,
then
,
then ![]() , then ... all the way to
, then ... all the way to ![]() .
Because of this consecutive term cancellation, this type of summation is called a "telescoping" sum. This cancellation will be shown in detail. First change the order of addition.)
.
Because of this consecutive term cancellation, this type of summation is called a "telescoping" sum. This cancellation will be shown in detail. First change the order of addition.)
![]()
![]()
(Now reassociate and collect "like" terms.)
![]()
![]()
![]()
![]()
(Recall that
![]() .)
.)
![]() .
.
Click HERE to return to the list of problems.
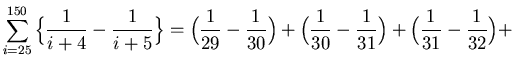
![]()
(This is a "telescoping" sum. Group "like" terms and cancel.)
![]()
![]()
![]()
![]()
![]()
![]() .
.
Click HERE to return to the list of problems.
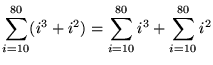
(The summations must begin with i=1 in order to use the given formulas.)
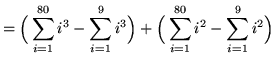
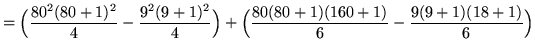
= 10,497,600 - 2025 + 173,880 - 285
= 10,669,170 .
Click HERE to return to the list of problems.
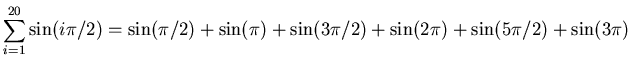
![]()
![]()
(Recall that
![]() if n is an integer.)
if n is an integer.)
![]()
![]()
(Recall that
![]() and
and
![]() .)
.)
= 1 + (-1) + 1 + (-1) + 1 + (-1) + 1 + (-1) + 1 + (-1)
= (1 + (-1)) + (1 + (-1)) + (1 + (-1)) + (1 + (-1)) + (1 + (-1))
= 0 + 0 + 0 + 0 + 0
= 0 .
Click HERE to return to the list of problems.
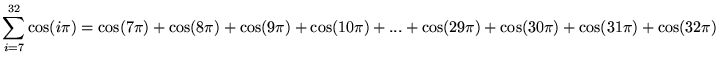
= ( (-1) + 1 ) + ( (-1) + 1 ) + ... + ( (-1) + 1 ) + ( (-1) + 1 )
= 0 + 0 + ... + 0 + 0
= 0 .
Click HERE to return to the list of problems.
There are several ways to prove that
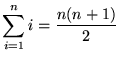 . This proof uses a telescoping sum. Consider the summation
. This proof uses a telescoping sum. Consider the summation
![$ \displaystyle{ \sum_{i=1}^{n} [ (i+1)^2 - i^2 ] } $](img42.gif) . It can be evaluated in two different ways.
First, treat it as a telescoping sum. Then
. It can be evaluated in two different ways.
First, treat it as a telescoping sum. Then
![$ \displaystyle{ \sum_{i=1}^{n} [ (i+1)^2 - i^2 ] } = (2^2 - 1^2) + (3^2 - 2^2) + (4^2 - 3^2) + (5^2 - 4^2) + ... + (n^2 - (n-1)^2) + ((n+1)^2 - n^2) $](img43.gif)
(Commute the addition.)
= (-12 + 22) + (-22 + 32) + (-32 + 42) + (-42 + 52) + ... + (-(n-1)2 + n2) + (-n2 + (n+1)2)
(Group "like" terms.)
= -12 + (22 - 22) + (32 - 32) + (42 - 42) + (52 - 52) + ... + ((n-1)2-(n-1)2) + (n2 - n2) + (n+1)2
= -12 + (0) + (0) + (0) + (0) + ... + (0) + (0) + (n+1)2
= (n+1)2 - 1
= n2 + 2n + 1 - 1
(*)
= n2 + 2n .
Second,
![$ \displaystyle{ \sum_{i=1}^{n} [ (i+1)^2 - i^2 ] }
= \displaystyle{ \sum_{i=1}^{n} [ i^2 + 2i + 1 - i^2 ] } $](img44.gif)
![$ = \displaystyle{ \sum_{i=1}^{n} [ 2i + 1 ] } $](img45.gif)
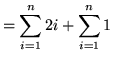
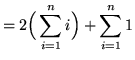
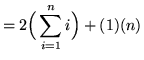
(**)
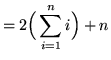 .
.
Equating expressions (*) and (**) we get that
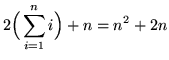 ,
,
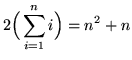 ,
,
or
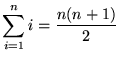 .
.
This completes the proof.
Click HERE to return to the list of problems.
There are several ways to prove that
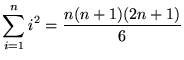 . This proof uses a telescoping sum. Consider the summation
. This proof uses a telescoping sum. Consider the summation
![$ \displaystyle{ \sum_{i=1}^{n} [ (i+1)^3 - i^3 ] } $](img53.gif) . It can be evaluated in two different ways.
First, treat it as a telescoping sum. Then
. It can be evaluated in two different ways.
First, treat it as a telescoping sum. Then
![$ \displaystyle{ \sum_{i=1}^{n} [ (i+1)^3 - i^3 ] } = (2^3 - 1^3) + (3^3 - 2^3) + (4^3 - 3^3) + (5^3 - 4^3) + ... + (n^3 - (n-1)^3) + ((n+1)^3 - n^3) $](img54.gif)
(Commute the addition.)
= (-13 + 23) + (-23 + 33) + (-33 + 43) + (-43 + 53) + ... + (-(n-1)3 + n3) + (-n3 + (n+1)3)
(Group "like" terms.)
= -13 + (23 - 23) + (33 - 33) + (43 - 43) + (53 - 53) + ... + ((n-1)3 - (n-1)3) + (n3 - n3) + (n+1)3
= -13 + (0) + (0) + (0) + (0) + ... + (0) + (0) + (n+1)3
= (n+1)3 - 1
= n3 + 3n2 + 3n + 1 - 1
(*)
= n3 + 3n2 + 3n .
Second,
![$ \displaystyle{ \sum_{i=1}^{n} [ (i+1)^3 - i^3 ] }
= \displaystyle{ \sum_{i=1}^{n} [ i^3 + 3i^2 + 3i + 1 - i^3 ] } $](img55.gif)
![$ = \displaystyle{ \sum_{i=1}^{n} [ 3i^2 + 3i + 1 ] } $](img56.gif)
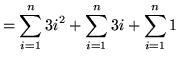
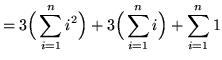
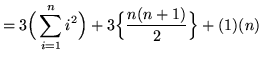
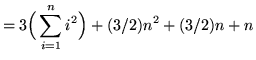
(**)
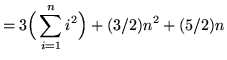 .
.
Equating expressions (*) and (**) we get that
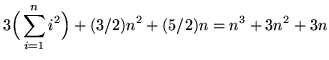 ,
,
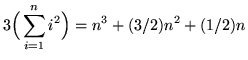 ,
,
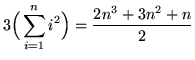 ,
,
or
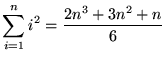
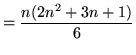
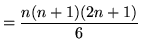 .
.
This completes the proof.
Click HERE to return to the list of problems.
There is one nonobvious, but simple step in the solution of this problem. It requires that you write a fraction as a sum or difference of partial fractions. For example,
![]()
is a partial fractions decomposition of
![]() . Then a partial fraction decomposition of
. Then a partial fraction decomposition of
![]() is
is
![]()
so that
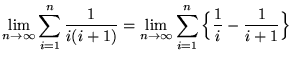
(This summation is a telescoping sum.)
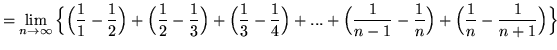
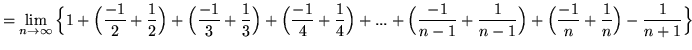
![]()
![]()
(Now evaluate the limit.)
= 1 - 0
= 1 .
Click HERE to return to the list of problems.
Note that in all of the following summations, letter i is a variable and letter n is a constant (until the limit is evaluated). Then
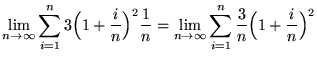
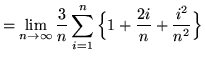
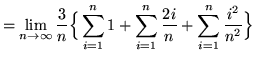
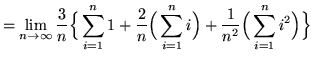
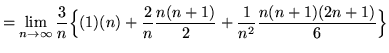
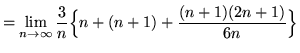
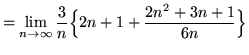
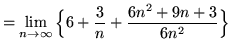
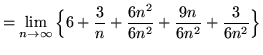
![]()
(Now evaluate the limit.)
= 6 + (0) + 1 + (0) + (0)
= 7 .
Click HERE to return to the list of problems.
The formula
4i -1 for i=1, 2, 3, 4, 5, ...
generates the given list of numbers. For example, the first number (i=1) in the list is
4(1)-1 = 3 .
The second number (i=2) in the list is
4(2)-1 = 7 .
The 30th number (i=30) in the list is
4(30)-1 = 119 .
The 120th number (i=12) in the list is
4(120)-1 = 479 .
Thus, the sum of the first 120 numbers in this list can now be computed as
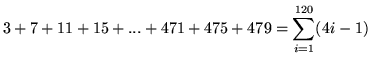
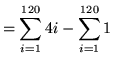
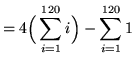
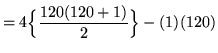
= 29,040 - 120
= 28,920 .
Click HERE to return to the list of problems.