Solution 1: Here is a carefully labeled sketch of the graph with a radius $r$ marked together with $x$ on the $x$-axis.
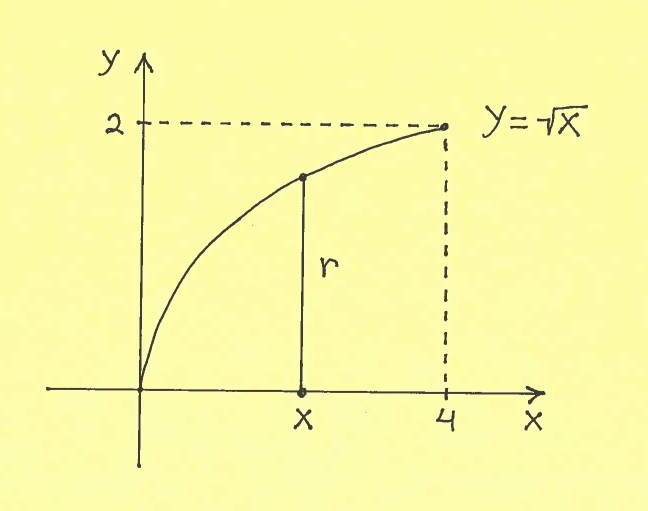
Thus the total Area of this Surface of Revolution is
$$ Surface \ Area = 2 \pi \int_{0}^{4} (radius) \sqrt{ 1 + \Big({dy \over dx}\Big)^2 } \ dx $$
$$ = 2 \pi \int_{0}^{4} (x^{1/2}) \sqrt{ 1 + ((1/2)x^{-1/2})^2 } \ dx $$
$$ = 2 \pi \int_{0}^{4} (x^{1/2}) \sqrt{ 1 + (1/4)x^{-1} } \ dx $$
$$ = 2 \pi \int_{0}^{4} (x^{1/2}) \sqrt{ 1 + {1 \over 4x} } \ dx $$
$$ = 2 \pi \int_{0}^{4} (x^{1/2}) \sqrt{ {4x \over 4x}+ {1 \over 4x} } \ dx $$
$$ = 2 \pi \int_{0}^{4} (x^{1/2}) \sqrt{ {4x +1 \over 4x} } \ dx $$
$$ = 2 \pi \int_{0}^{4} (x^{1/2}) { \sqrt{ 4x +1 } \over \sqrt{4x} } \ dx $$
$$ = 2 \pi \int_{0}^{4} (x^{1/2}) { \sqrt{ 4x +1 } \over 2 x^{1/2} } \ dx $$
$$ = 2 \pi \int_{0}^{4} { \sqrt{ 4x +1 } \over 2 } \ dx $$
$$ = {2 \pi \over 2 } \int_{0}^{4} \sqrt{ 4x +1 } \ dx $$
$$ = \pi \cdot {2 \over 3} \cdot {1 \over 4} (4x+1)^{3/2} \Big|_{0}^{4} $$
$$ = { \pi \over 6 } (4x+1)^{3/2} \Big|_{0}^{4} $$
$$ = { \pi \over 6 } \Big( (4(4)+1)^{3/2} - (4(0)+1)^{3/2} \Big) $$
$$ = { \pi \over 6 } \Big( (17)^{3/2} - (1)^{3/2} \Big) $$
$$ = { \pi \over 6 } \Big( (17)^{3/2} - 1 \Big) $$
Click HERE to return to the list of problems.

