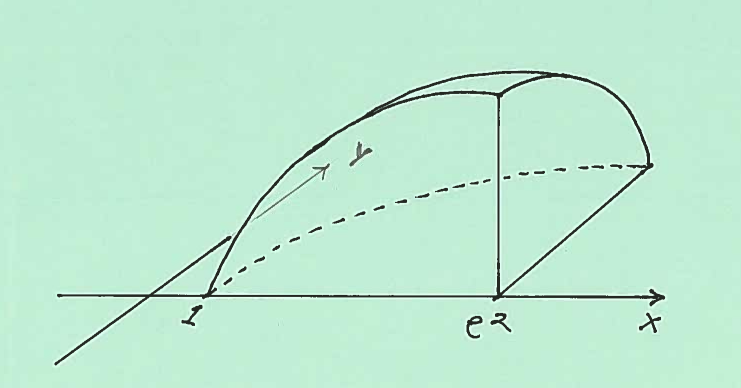
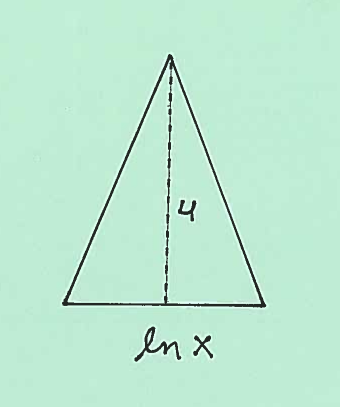SOLUTION 2: a.) Here are sketches of the base of the solid and the entire solid.
 $ \ \ \ $
$ \ \ \ $
Here are sketches of a square cross-section at $x$, together with it's dimensions.
 $ \ \ \ $
$ \ \ \ $
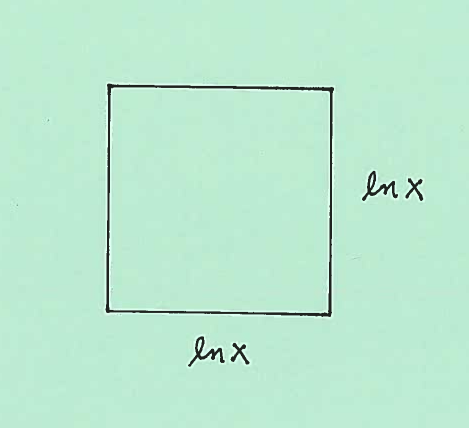
The area of the square cross-section is $ A(x)= (edge)^2 = (\ln x)^2 $. Thus the total volume of this static solid is
$$ Volume = \int_{1}^{e^2} (\ln x)^2 \ dx $$
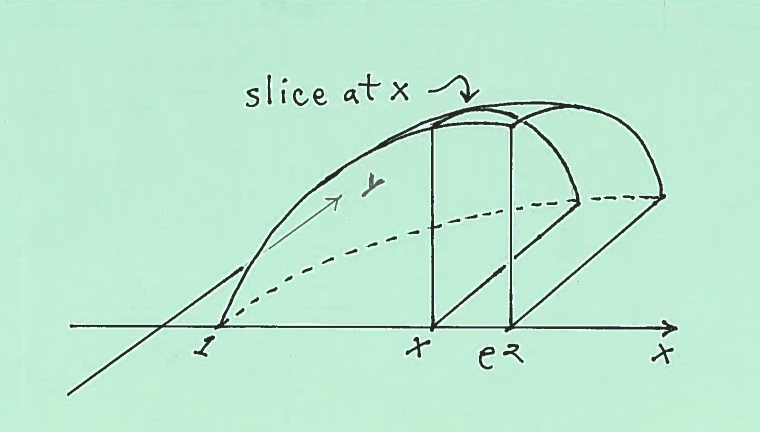
SOLUTION 2: b.) Here are sketches of the base of the solid and the entire solid.
 $ \ \ \ $
$ \ \ \ $
Here are sketches of a quarter-circular cross-section at $x$, together with its radius.
 $ \ \ \ $
$ \ \ \ $
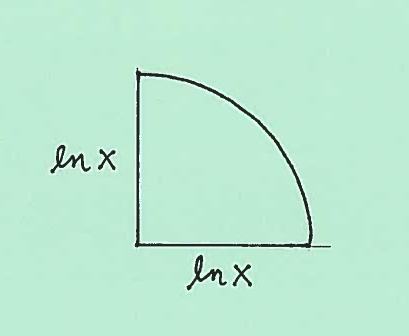
The area of the quarter-circular cross-section is $ A(x)= { 1 \over 4 } \pi r^2 = { 1 \over 4 } \pi (\ln x)^2 $. Thus the total volume of this static solid is
$$ Volume = \int_{1}^{e^2} { 1 \over 4 } \pi (\ln x)^2 \ dx $$
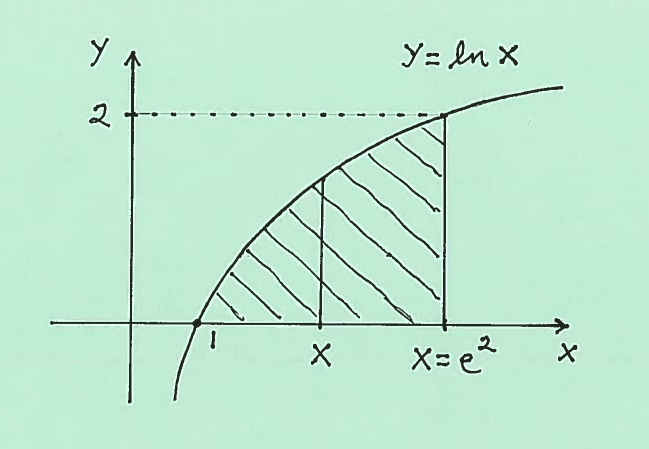
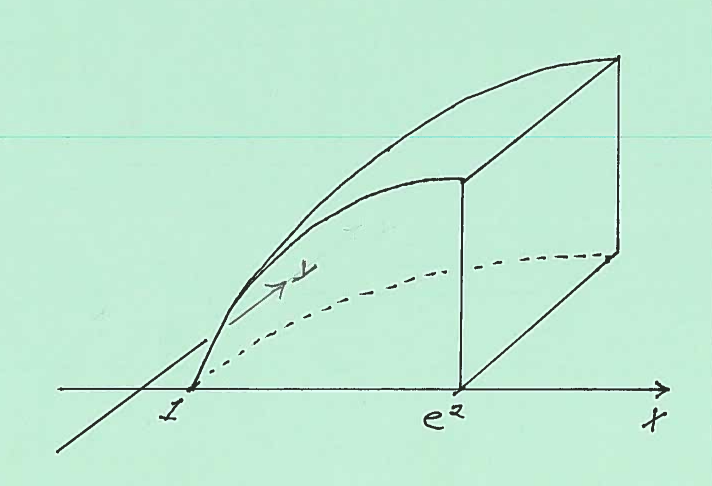
SOLUTION 2: c.) Here are sketches of the base of the solid and the entire solid.
 $ \ \ \ $
$ \ \ \ $
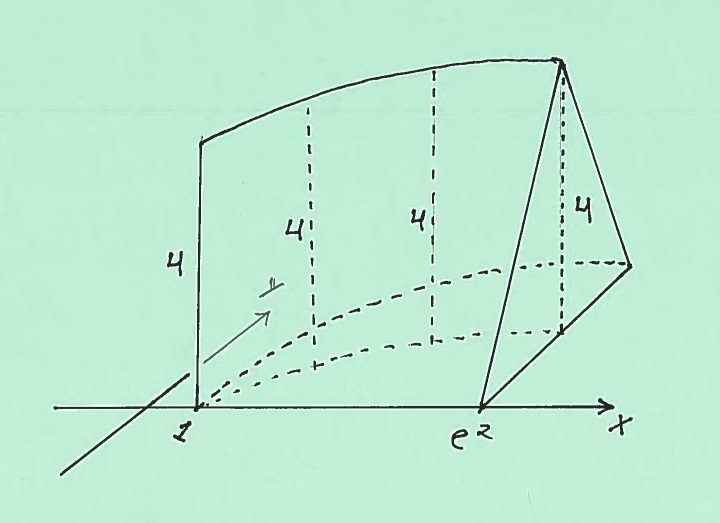
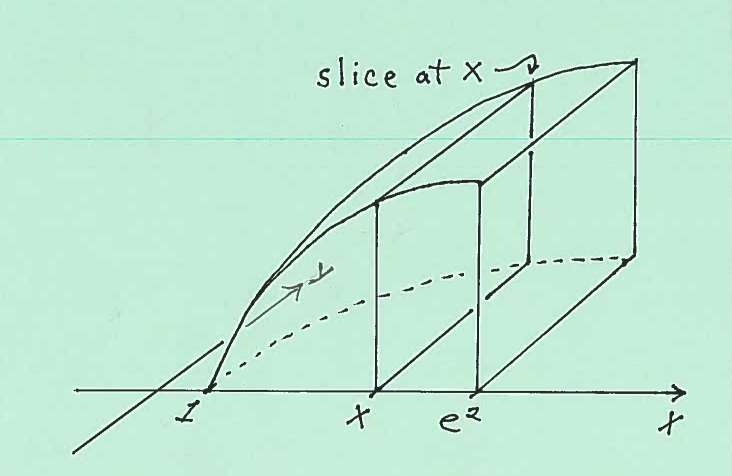
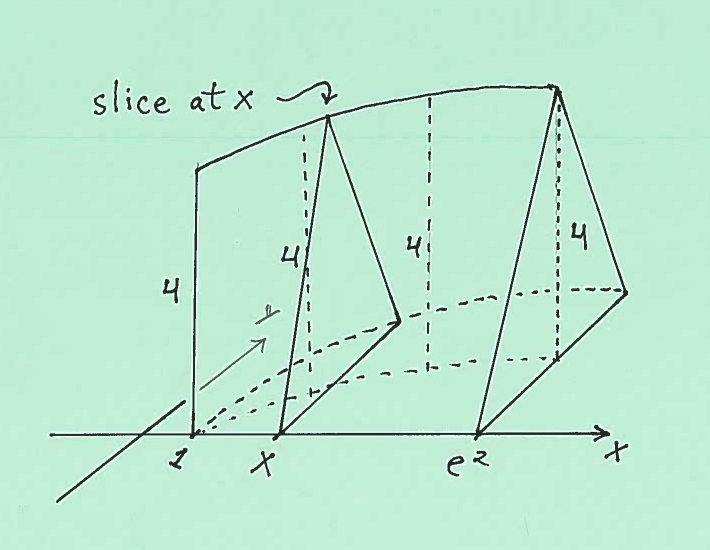
Here are sketches of an isosceles triangular cross-section at $x$, together with its dimensions.
 $ \ \ \ $
$ \ \ \ $
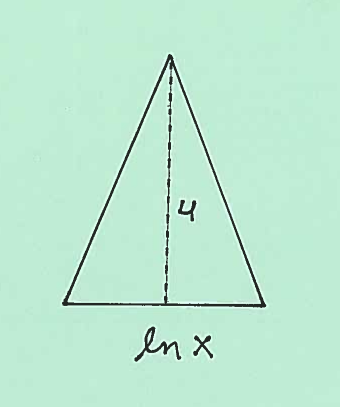
The area of the isosceles triangular cross-section is $ A(x)= { 1 \over 2 }(base)(height) = { 1 \over 2 }(\ln x)(4) = 2 \ln x $. Thus the total volume of this static solid is
$$ Volume = \int_{1}^{e^2} 2 \ln x \ dx $$
Click HERE to return to the list of problems.
 $ \ \ \ $
$ \ \ \ $

 $ \ \ \ $
$ \ \ \ $

 $ \ \ \ $
$ \ \ \ $

 $ \ \ \ $
$ \ \ \ $

 $ \ \ \ $
$ \ \ \ $
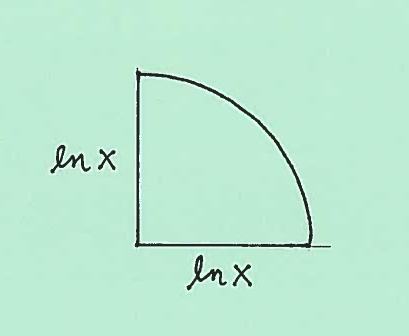
 $ \ \ \ $
$ \ \ \ $

 $ \ \ \ $
$ \ \ \ $