The Proof Page
by D. A. Kouba
Section 1.1- Propositions and Connectives; Truth Tables
In the study of mathematics, one often must begin with definitions and assumptions (rules of the game), which are assumed to be true. The process of deductive reasoning can then lead to logical conclusions (lemmas, theorems, and corollaries), which need to be proven true. In general, unique or uniform mathematical language and symbols are used to simplify this process. The Proof Page will assist those in the transition from ``how to" mathematics to ``why" mathematics.
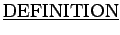 : A
: A
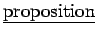 is a sentence that is either true (T) or false (F).
is a sentence that is either true (T) or false (F).
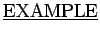 : Determine which of the following sentences are propositions. Find solutions HERE .
: Determine which of the following sentences are propositions. Find solutions HERE .
- 1.) The numbers 3 and 11 are prime.
- 2.) The sun rises in the West and sets in the East.
- 3.)
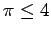
- 4.)
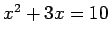
- 5.) If
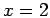 , then
, then 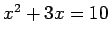
- 6.) If
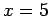 , then
, then 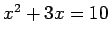
- 7.) Barry Bonds will hit at least 60 homeruns this baseball season.
- 8.) Buy a carton of milk on the way home today.
- 9.) You will buy a carton of milk on the way home today.
- 10.) Bill Clinton was a popular president.
- 11.) Where are the children ?
- 12.) Beethoven was born on a Tuesday.
We will now begin combining propositions using the symbols 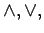 and
and 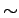 , which are called logical connectives.
, which are called logical connectives.
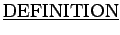 : Let
: Let 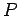 and
and 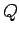 be propositions.
be propositions.
1.) The
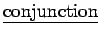 of
of  and
and 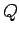 is written
is written 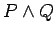 (read ``
(read ``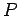 and
and 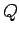 "). The conjunction is true exactly when both
"). The conjunction is true exactly when both 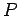 and
and 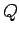 are true.
are true.
2.) The
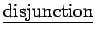 of
of  and
and 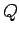 is written
is written 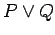 (read ``
(read ``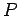 or
or 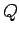 "). The disjunction is true exactly when at least one of
"). The disjunction is true exactly when at least one of 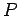 and
and 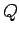 is true.
is true.
3.) The
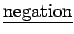 of
of 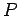 is written
is written 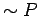 (read ``not
(read ``not 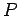 "). The negation is true exactly when
"). The negation is true exactly when 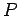 is false.
is false.
NOTE : The preceding three definitions of logical connectives and their values of true (T) and false (F) are designed to be consistent with standard spoken and written usage of ``and", ``or", and ``not" in the English language.
 : A
: A
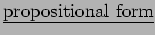 is an expression involving finitely many logical symbols (connectives) and letters (propositions).
is an expression involving finitely many logical symbols (connectives) and letters (propositions).
 : The expression
: The expression
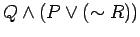 is a propositional form.
is a propositional form.
The following truth tables illustrate all possible truth values for the propositional forms 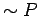 ,
, 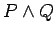 , and
, and 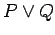 .
.
On The Proof Page, in particular, and in advanced mathematics, in general, we are often concerned with the equivalence of mathematical statements, that is, the equivalence of propositional forms. Equivalent forms give us the opportunity to choose, from among all the equivalent forms, a form which is simplest to use or easiest to understand. Propositional forms are equivalent if they have the same truth tables.
 :
Determine if the following propositional forms are equivalent.
:
Determine if the following propositional forms are equivalent.
- 1.)
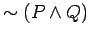 and
and
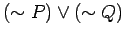 .............Find solution HERE .
.............Find solution HERE .
- 2.)
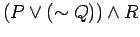 and
and
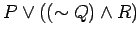 .............Find solution HERE .
.............Find solution HERE .
- 3.)
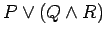 and
and
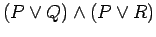 .............Find solution HERE .
.............Find solution HERE .
NOTE : (ORDER OF OPERATIONS) If parantheses are not used to clearly indicate the use of the connectives, then invoke the connectives in the following order- 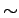 ,
, 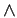 ,
, 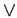 . For example,
. For example,
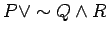 is equivalent to
is equivalent to
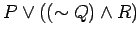 .
.
 : Provide parantheses to clarify the following ambiguous expressions. Find solutions HERE .
: Provide parantheses to clarify the following ambiguous expressions. Find solutions HERE .
 : A
: A
 is a propositional form for which all of its values are true (T). A
is a propositional form for which all of its values are true (T). A
 is a propositional form for which all of its values are false.
is a propositional form for which all of its values are false.
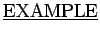 : Truth tables can be used to easily verify the following two statements. The form
: Truth tables can be used to easily verify the following two statements. The form
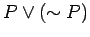 is a tautology. The form
is a tautology. The form
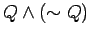 is a contradiction.
is a contradiction.
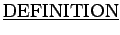 : A
: A
 of a proposition
of a proposition 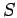 is any proposition which is equivalent to
is any proposition which is equivalent to 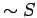 .
.
 : Let proposition
: Let proposition 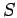 be ``Integer
be ``Integer 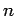 is even." Each of the following statements is a denial of
is even." Each of the following statements is a denial of 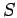 , that is, each statemnt is equivalent to
, that is, each statemnt is equivalent to 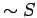 .
.
1.) It is not the case that integer 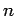 is even.
is even.
2.) Integer 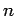 is not even.
is not even.
3.) Integer 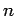 is odd.
is odd.
4.) Integer 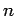 can be written in the form
can be written in the form 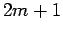 , where
, where 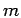 is some integer.
is some integer.
5.) Integer 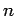 can be written in the form
can be written in the form 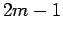 , where
, where 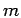 is some integer.
is some integer.
 : Write two denials for each proposition. Find solutions HERE .
: Write two denials for each proposition. Find solutions HERE .
- 1.) Integer
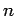 is odd.
is odd.
- 2.) You are beautiful and you drive a fast car.
- 3.) He is tired or hungry.
- 4.) Some dogs chase cats.
- 5.) All men love to watch football.
- 6.) If you are a woman, then you are good at calculus.
- 7.) If you are a college student, then you eat pizza and play video games.
RETURN to The Proof Page .
Please e-mail your comments, questions, or suggestions to D. A. Kouba at
kouba@math.ucdavis.edu .
Next: About this document ...
Duane Kouba
2002-05-08