The Proof Page
by D. A. Kouba
Section 1.3- Universal Quantifier (For all x ...); Existential Quantifier (There exists x ...); Unique Existential Quantifier (There exists a unique x ...)
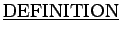 : A sentence containing one or more variables is called an
: A sentence containing one or more variables is called an
 .
.
 : An open sentence is NOT a proposition because it is neither true nor false until all of its variables are replaced with values.
: An open sentence is NOT a proposition because it is neither true nor false until all of its variables are replaced with values.
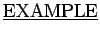 : The expression
: The expression 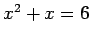 is an open sentence. Define
is an open sentence. Define 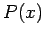 to be the open sentence
to be the open sentence 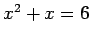 . Then
. Then 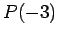 means
means 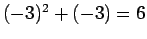 , which is a true proposition, and
, which is a true proposition, and 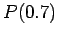 means
means
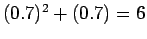 , which is a false proposition.
, which is a false proposition.
 : Define
: Define 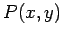 to be the open sentence
to be the open sentence 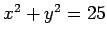 . Then
. Then 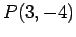 means
means
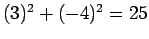 , which is a true proposition, and
, which is a true proposition, and 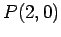 means
means
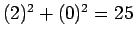 , which is a false proposition.
, which is a false proposition.
 : The set of objects
: The set of objects 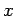 (or
(or 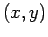 ) available for consideration (substitution) in an open sentence
) available for consideration (substitution) in an open sentence 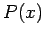 (or
(or 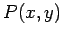 ) is called a
) is called a
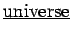 . The set of elements
. The set of elements 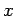 (or
(or 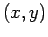 ) which makes
) which makes 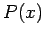 (or
(or 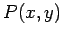 ) true is called the
) true is called the
 .
.
 : Let the universe be the set of all real numbers for the open sentence
: Let the universe be the set of all real numbers for the open sentence
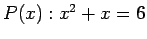 . Then the truth set is
. Then the truth set is 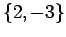 . Let the universe be the set of all positive integers for the open sentence
. Let the universe be the set of all positive integers for the open sentence
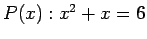 . Then the truth set is
. Then the truth set is 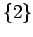 .
.
 : Let
: Let 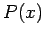 be an open sentence with variable
be an open sentence with variable 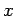 .
.
- 1.) The
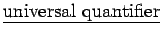 is the sentence
is the sentence
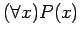 (`` For all
(`` For all 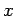 ,
, 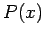 ") and is true exactly when the truth set for
") and is true exactly when the truth set for 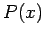 is the entire universe. In other words, all elements in the universe make
is the entire universe. In other words, all elements in the universe make 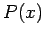 true.
true.
- 2.) The
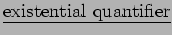 is the sentence
is the sentence
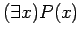 (`` There exists
(`` There exists 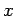 such that
such that 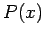 ") and is true exactly when the truth set for
") and is true exactly when the truth set for 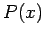 is not empty. In other words, there exists at least one element
is not empty. In other words, there exists at least one element 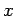 in the universe for which
in the universe for which 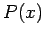 is true.
is true.
- 3.) The
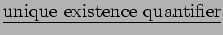 is the sentence
is the sentence
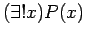 (`` There exists a unique
(`` There exists a unique 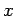 such that
such that 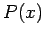 ") and is true exactly when the truth set for
") and is true exactly when the truth set for 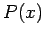 has exactly one element. In other words, there exists exactly one element
has exactly one element. In other words, there exists exactly one element 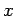 in the universe for which
in the universe for which 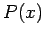 is true.
is true.
The previous definitions of quantifiers are somewhat abstract and technical, and may appear to be fairly msysterious. However, careful examination of the following examples will likely make them very understandable.
 :
:
- 1.) Let the universe be the set of all real numbers and consider the open sentence
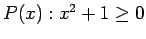 . Consider the quantified sentence
. Consider the quantified sentence
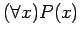 . This sentence is true since it is true for every element in the universe.
. This sentence is true since it is true for every element in the universe.
- 2.) Let the universe be the set of all complex numbers and consider the open sentence
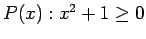 . Consider the quantified sentence
. Consider the quantified sentence
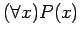 . This sentence is false since it is false for some elements in the universe. For example,
. This sentence is false since it is false for some elements in the universe. For example, 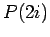 is false since
is false since
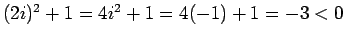 .
.
- 3.) Let the universe be the set of all real numbers and consider the open sentence
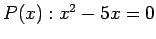 . Consider the quantified sentence
. Consider the quantified sentence
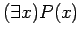 . This sentence is true since it is true for at least one element in the universe. In fact, the truth set is
. This sentence is true since it is true for at least one element in the universe. In fact, the truth set is 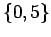 .
.
- 4.) Let the universe be the set of all real numbers and consider the open sentences
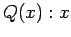 is an integer, and
is an integer, and 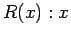 is a perfect square. Consider the quantified sentence
is a perfect square. Consider the quantified sentence
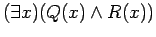 . This sentence is true since it is true for at least one element in the universe. For example,
. This sentence is true since it is true for at least one element in the universe. For example, 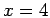 and
and 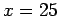 make the sentence true. The truth set contains infinitely many elements.
make the sentence true. The truth set contains infinitely many elements.
- 5.) (Pay close attention to the logic in this example.) Let the universe be the set of all real numbers and consider the open sentences
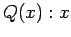 is a natural number, and
is a natural number, and 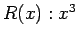 is a natural number. Consider the quantified sentence
is a natural number. Consider the quantified sentence
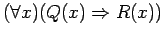 . This sentence is true since it is true for every element in the universe ! For example, if
. This sentence is true since it is true for every element in the universe ! For example, if 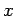 is a natural number, then
is a natural number, then
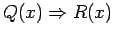 is a true statement since both
is a true statement since both 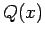 and
and 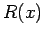 are true. If
are true. If 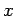 is NOT a natural number, then
is NOT a natural number, then
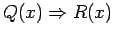 is a still a true statement since
is a still a true statement since 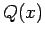 is false ! Thus,
is false ! Thus,
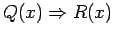 is a true statement for every element in the universe.
is a true statement for every element in the universe.
- 6.) Let the universe be the set of all real numbers and consider the open sentence
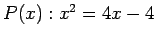 . Consider the quantified sentence
. Consider the quantified sentence
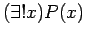 . This sentence is true since it is true for exactly one element in the universe. It is true for
. This sentence is true since it is true for exactly one element in the universe. It is true for 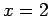 .
.
- 7.) Let the universe be the set of all real numbers and consider the open sentence
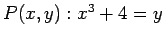 . Consider the quantified sentence
. Consider the quantified sentence
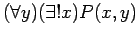 . This sentence is true (since
. This sentence is true (since 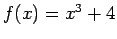 is an increasing function). If
is an increasing function). If 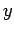 is any element in the universe, then
is any element in the universe, then
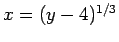 is the unique solution to
is the unique solution to 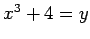 .
.
 : In general, QUANTIFIERS DO NOT COMMUTE. In Example 7 just completed,
: In general, QUANTIFIERS DO NOT COMMUTE. In Example 7 just completed,
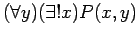 and
and
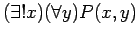 have distinct meanings. The statement
have distinct meanings. The statement
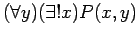 is already explained. The statement
is already explained. The statement
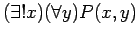 means that there is a single, unique real number
means that there is a single, unique real number 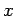 so that
so that 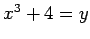 for all real numbers
for all real numbers 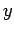 . In fact, this second statement is false.
. In fact, this second statement is false.
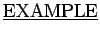 : Let the universe be the set of all animals. Consider the open sentences
: Let the universe be the set of all animals. Consider the open sentences 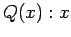 is a dog,
is a dog, 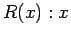 chases cars, and
chases cars, and 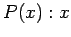 eats vegetables. Rewrite each of the following common sentences in symbolic quantifier form. Find solutions HERE .
eats vegetables. Rewrite each of the following common sentences in symbolic quantifier form. Find solutions HERE .
- 1.) Some dogs eat vegetables.
- 2.) All dogs chase cars.
- 3.) No dogs chase cars.
- 4.) There are some animals which chase cars but do not eat vegetables.
 : Write a logical, meaningful denial of each sentence in ordinary English. Find solutions HERE .
: Write a logical, meaningful denial of each sentence in ordinary English. Find solutions HERE .
- 1.) Some cats like water.
- 2.) Some cats don't like water.
- 3.) No cats like water.
- 4.) All cats like water.
The following theorem formally addresses the negation of quantified sentences.
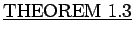 : Let
: Let 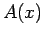 be an open sentence with variable
be an open sentence with variable 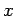 .
.
- a.)
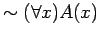 is equivalent to
is equivalent to
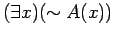 .
.
- b.)
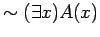 is equivalent to
is equivalent to
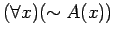 .
.
 : a.) (NOTATION : Assume that ``
: a.) (NOTATION : Assume that ``
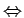 " has the same meaning as `` if and only if " has the same meaning as `` iff .")
We will show that
" has the same meaning as `` if and only if " has the same meaning as `` iff .")
We will show that
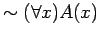 and
and
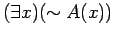 have the same truth values.
First,
have the same truth values.
First,
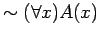 is TRUE
is TRUE
iff
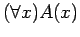 is FALSE
is FALSE
iff
The truth set for 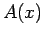 is NOT the entire universe
is NOT the entire universe
iff
There is at least one element in the truth set for which 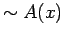
iff
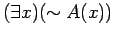 is TRUE .
is TRUE .
Second,
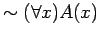 is FALSE
is FALSE
iff
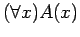 is TRUE
is TRUE
iff
The truth set for 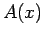 is the entire universe
is the entire universe
iff
The truth set for 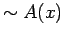 is empty
is empty
iff
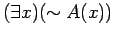 is FALSE.
is FALSE.
Thus,
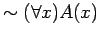 and
and
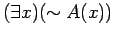 have the same truth values.
have the same truth values.
b.) The proof that
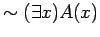 is equivalent to
is equivalent to
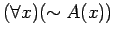 is analogous to the proof of part a.).
is analogous to the proof of part a.).
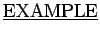 : Let the universe be the set of all animals. Consider the open sentences
: Let the universe be the set of all animals. Consider the open sentences  is a dog ,
is a dog , 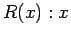 chases cars, and
chases cars, and 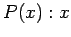 eats vegetables. Rewrite each of the following common sentences in symbolic quantifier form. Use Theorems 1.2 and 1.3 to write formal denials of these statements. Finish by writing a meaningful denial in ordinary English. Find solutions HERE .
eats vegetables. Rewrite each of the following common sentences in symbolic quantifier form. Use Theorems 1.2 and 1.3 to write formal denials of these statements. Finish by writing a meaningful denial in ordinary English. Find solutions HERE .
- 1.) Some dogs eat vegetables.
- 2.) All dogs chase cars.
- 3.) No dogs chase cars.
- 4.) There are some animals, which chase cars but do not eat vegetables.
 : In calculus we learn that if function
: In calculus we learn that if function 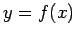 is continuous at
is continuous at 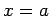 , then the following formal
, then the following formal
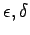 definition is true. For every real number
definition is true. For every real number 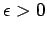 there exists another real number
there exists another real number 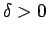 so that if
so that if
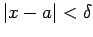 , then
, then
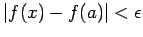 . Without loss of generality and for the sake of relative simplicity, assume that
. Without loss of generality and for the sake of relative simplicity, assume that 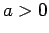 and let the universe be the set of all positive real numbers. Consider the open sentences
and let the universe be the set of all positive real numbers. Consider the open sentences
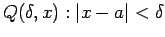 and
and
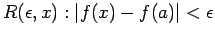 . We can now rewrite the
. We can now rewrite the
 definition in symbolic quantifier form as
definition in symbolic quantifier form as
![$ ( \forall \epsilon )( \exists \delta ) [ ( \forall x ) \{ Q( \delta, x) \Rightarrow R( \epsilon, x) \} ] $](img75.png) .
.
Next we will use Theorems 1.2 and 1.3 to write a formal denial of this statement, distributing the negation as far as possible, and finish by writing a meaningful denial in ordinary English. Then
![$ \sim ( \forall \epsilon )( \exists \delta ) [ ( \forall x ) \{ Q( \delta, x) \Rightarrow R( \epsilon, x) \} ] $](img76.png)
iff
![$ ( \exists \epsilon ) \sim ( \exists \delta ) [ ( \forall x ) \{ Q( \delta, x) \Rightarrow R( \epsilon, x) \} ] $](img77.png) . . . . . . (By Theorem 1.3 a.)
. . . . . . (By Theorem 1.3 a.)
iff
![$ ( \exists \epsilon ) ( \forall \delta ) \sim [ ( \forall x ) \{ Q( \delta, x) \Rightarrow R( \epsilon, x) \} ] $](img78.png) . . . . . . (By Theorem 1.3 b.)
. . . . . . (By Theorem 1.3 b.)
iff
![$ ( \exists \epsilon ) ( \forall \delta ) [ \sim ( \forall x ) \{ Q( \delta, x) \Rightarrow R( \epsilon, x) \} ] $](img79.png)
iff
![$ ( \exists \epsilon ) ( \forall \delta ) [ ( \exists x ) \sim \{ Q( \delta, x) \Rightarrow R( \epsilon, x) \} ] $](img80.png)
iff
![$ ( \exists \epsilon ) ( \forall \delta ) [ ( \exists x ) \sim \{ R( \epsilon, x) \vee \sim Q( \delta, x) \} ] $](img81.png) . . . . . . (By Theorem 1.2 d.)
. . . . . . (By Theorem 1.2 d.)
iff
![$ ( \exists \epsilon ) ( \forall \delta ) [ ( \exists x ) \{ \sim R( \epsilon, x) \wedge Q( \delta, x) \} ] $](img82.png) . . . . . . (By Theorem 1.2 c.)
. . . . . . (By Theorem 1.2 c.)
iff
There exists an 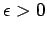 so that, for all
so that, for all 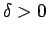 , there exists a real number
, there exists a real number 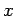 satisfying
satisfying
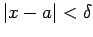 but
but
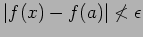 .
.
 : Write each of the following statements in symbolic quantifier form. Write a denial in symbolic quantifier form, distributing the negation as far as possible. Finish by writing a meaningful denial in ordinary English. Let the universe be the set of all real numbers. Find solutions HERE .
: Write each of the following statements in symbolic quantifier form. Write a denial in symbolic quantifier form, distributing the negation as far as possible. Finish by writing a meaningful denial in ordinary English. Let the universe be the set of all real numbers. Find solutions HERE .
- 1.) For all real numbers
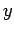 there is another real number
there is another real number 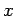 so that
so that 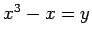 . Consider the open sentence
. Consider the open sentence
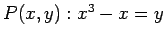 .
.
- 2.) For each real number
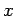 there is another real number
there is another real number 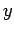 so that if
so that if 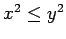 , then
, then 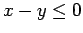 or
or 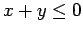 . Consider the open sentences
. Consider the open sentences
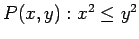 ,
,
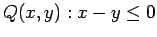 , and
, and
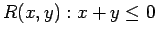 .
.
RETURN to The Proof Page .
Please e-mail your comments, questions, or suggestions to D. A. Kouba at
kouba@math.ucdavis.edu .
Next: About this document ...
Duane Kouba
2002-06-05
![]() : A sentence containing one or more variables is called an
: A sentence containing one or more variables is called an
![]() .
.
![]() : An open sentence is NOT a proposition because it is neither true nor false until all of its variables are replaced with values.
: An open sentence is NOT a proposition because it is neither true nor false until all of its variables are replaced with values.
![]() : The expression
: The expression ![]() is an open sentence. Define
is an open sentence. Define ![]() to be the open sentence
to be the open sentence ![]() . Then
. Then ![]() means
means ![]() , which is a true proposition, and
, which is a true proposition, and ![]() means
means
![]() , which is a false proposition.
, which is a false proposition.
![]() : Define
: Define ![]() to be the open sentence
to be the open sentence ![]() . Then
. Then ![]() means
means
![]() , which is a true proposition, and
, which is a true proposition, and ![]() means
means
![]() , which is a false proposition.
, which is a false proposition.
![]() : The set of objects
: The set of objects ![]() (or
(or ![]() ) available for consideration (substitution) in an open sentence
) available for consideration (substitution) in an open sentence ![]() (or
(or ![]() ) is called a
) is called a
![]() . The set of elements
. The set of elements ![]() (or
(or ![]() ) which makes
) which makes ![]() (or
(or ![]() ) true is called the
) true is called the
![]() .
.
![]() : Let the universe be the set of all real numbers for the open sentence
: Let the universe be the set of all real numbers for the open sentence
![]() . Then the truth set is
. Then the truth set is ![]() . Let the universe be the set of all positive integers for the open sentence
. Let the universe be the set of all positive integers for the open sentence
![]() . Then the truth set is
. Then the truth set is ![]() .
.
![]() : Let
: Let ![]() be an open sentence with variable
be an open sentence with variable ![]() .
.
![]() is TRUE
is TRUE
![]() is FALSE
is FALSE
![]() is NOT the entire universe
is NOT the entire universe
![]()
![]() is TRUE .
is TRUE .
![]() is FALSE
is FALSE
![]() is TRUE
is TRUE
![]() is the entire universe
is the entire universe
![]() is empty
is empty
![]() is FALSE.
is FALSE.
![]() .
.
![]()
![]() . . . . . . (By Theorem 1.3 a.)
. . . . . . (By Theorem 1.3 a.)
![]() . . . . . . (By Theorem 1.3 b.)
. . . . . . (By Theorem 1.3 b.)
![]()
![]()
![]() . . . . . . (By Theorem 1.2 d.)
. . . . . . (By Theorem 1.2 d.)
![]() . . . . . . (By Theorem 1.2 c.)
. . . . . . (By Theorem 1.2 c.)
![]() so that, for all
so that, for all ![]() , there exists a real number
, there exists a real number ![]() satisfying
satisfying
![]() but
but
![]() .
.