The Proof Page
by D. A. Kouba
Section 1.4- Bacic Proof Methods I- Direct Proof, Proof by Cases, and Proof by Working Backward
In this section we will introduce specific types or methods of proof of mathematical statements. They include direct proof, proof by cases, and proof by working backward. We will use the following well known facts :
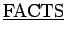 :
:
- 1. Integer
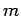 is even if
is even if 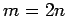 for some integer
for some integer 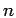 .
.
- 2. Integer
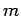 is odd if
is odd if 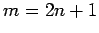 for some integer
for some integer 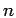 .
.
- 3. Integer
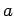 divides integer
divides integer 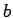 , written ,
, written , 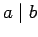 , if
, if 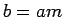 for some integer
for some integer 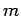 . NOTE : This definition applies only to integers.
. NOTE : This definition applies only to integers.
- 4. Natural number (positive integer)
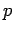 is prime if its only natural number factors are
is prime if its only natural number factors are 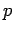 and
and 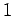 .
truein
.
truein
- 5. The absolute value of a real number
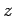 , written
, written 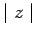 , is defined in the following way :
, is defined in the following way :
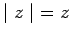 if
if 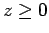 ;
;
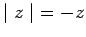 if
if 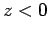 .
.
DIRECT PROOF
The direct proof of a mathematical statement should include the following.
- 1. Begin with a clear written statement of the given facts or assumptions.
- 2. Next provide a clear written statement of what is to be proven.
- 3. Then write the body of the proof, a sequence of logical steps or consequences leading to the desired result. Provide clear reasoning or substantiation for each step in the proof. A good rule of thumb is this. Treat each proof that you write as a writing exercise as well as a mathematical exercise. Remember that you are trying to convince your reader of the validity of your proof through the clarity and simplicity of your organization and logical reasoning. Finish your proof with a clear statement of that which was to be proven. (Many proofs are closed with the letters QED. This refers to the Latin ``quod est demonstratum," roughly meaning ``which is proven or demonstrated.") Shortcuts in proofs are to be avoided at this stage. Writing more details is better for those of you who are just learning how to write proofs.
Here is a simple example of a direct proof.
 : Prove that if
: Prove that if 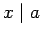 and
and 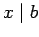 , then
, then
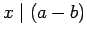 .
.
Proof: ASSUME that 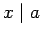 and
and 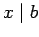 . Thus
. Thus 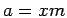 and
and 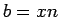 for some integers
for some integers 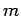 and
and 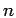 . SHOW that
. SHOW that 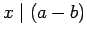 , i.e., show that
, i.e., show that 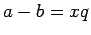 for some integer
for some integer 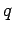 . Then
. Then
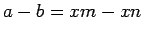 (by assumptions)
(by assumptions)
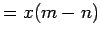 (by distributive property)
(by distributive property)
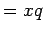 ,
,
where 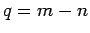 is an integer. Thus,
is an integer. Thus, 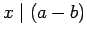 .
.
QED
Here is another example of a direct proof.
 : Prove that if
: Prove that if 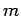 is even and
is even and 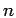 is odd, then
is odd, then
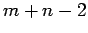 is odd .
is odd .
Proof: ASSUME that 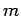 is even and
is even and 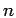 is odd. Thus
is odd. Thus 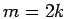 and
and 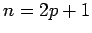 for some integers
for some integers 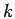 and
and 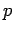 . SHOW that
. SHOW that 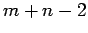 is odd, i.e., show that
is odd, i.e., show that 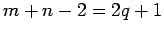 for some integer
for some integer 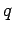 . Then
. Then
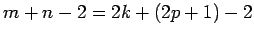 (by assumptions)
(by assumptions)
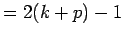 (by distributive property)
(by distributive property)
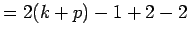 (adding zero)
(adding zero)
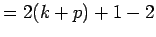
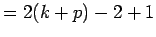 (by commutative property)
(by commutative property)
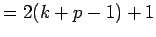 (by distributive property)
(by distributive property)
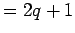 ,
,
where 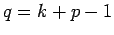 is an integer. Thus,
is an integer. Thus, 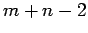 is odd.
is odd.
QED
 : Write clear and complete direct proofs for each of the following mathematical statements. Find solutions HERE : Page 1 , Page 2 .
: Write clear and complete direct proofs for each of the following mathematical statements. Find solutions HERE : Page 1 , Page 2 .
- 1. If
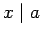 and
and 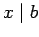 , then
, then
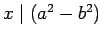 .
.
- 2. If
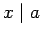 and
and 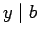 , then
, then
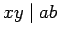 .
.
- 3. If
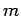 is even and
is even and 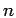 is odd, then
is odd, then
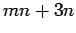 is odd .
is odd .
- 4. If
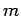 is odd, then
is odd, then 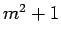 is even .
is even .
PROOF BY CASES
A proof by cases of a mathematical statement should include the following.
- 1. Begin with a clear written statement of the given facts or assumptions.
- 2. Next provide a clear written statement of what is to be proven.
- 3. Now determine all possible cases which must be considered in order to prove the mathematical statement.
- 4. Then write the body of the proof. For each case, this must include a sequence of logical steps or consequences leading to the desired result. Provide clear reasoning or substantiation for each step in the proof. A good rule of thumb is this. Treat each proof that you write as a writing exercise as well as a mathematical exercise. Remember that you are trying to convince your reader of the validity of your proof through the clarity and simplicity of your organization and logical reasoning. Finish your proof with a clear statement of that which was to be proven. Shortcuts in proofs are to be avoided at this stage. Writing more details is better for those of you who are just learning how to write proofs.
Here is a simple example of a proof by cases.
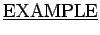 : Prove that if
: Prove that if 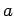 and
and 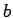 are real numbers, where
are real numbers, where 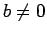 , then
, then
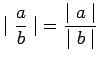 .
.
Proof: ASSUME that 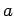 and
and 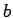 are real numbers and
are real numbers and 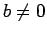 . SHOW that
. SHOW that
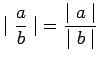 . We will consider the following cases.
. We will consider the following cases.
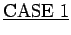 : Assume that
: Assume that 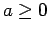 and
and 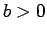 , so that
, so that
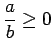 . Then
. Then
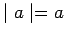 ,
,
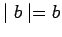 , and
, and
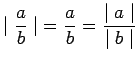 .
.
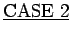 : Assume that
: Assume that 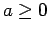 and
and 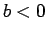 , so that
, so that
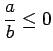 . Then
. Then
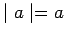 ,
,
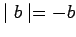 , and
, and
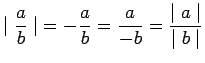 .
.
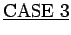 : Assume that
: Assume that 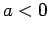 and
and 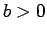 , so that
, so that
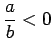 . Then
. Then
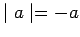 ,
,
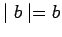 , and
, and
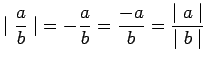 .
.
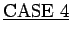 : Assume that
: Assume that 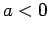 and
and 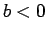 , so that
, so that
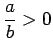 . Then
. Then
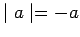 ,
,
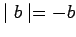 , and
, and
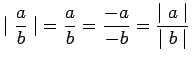 .
.
Thus, for all possible cases, it has been proven that
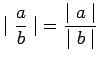 .
.
QED
Here is another example of a proof by cases.
 : Prove that
: Prove that
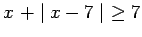 for all real numbers
for all real numbers 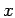 .
.
Proof: ASSUME that 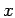 is a real number. SHOW that
is a real number. SHOW that
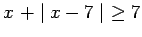 . We will consider the following cases.
. We will consider the following cases.
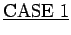 : Assume that
: Assume that 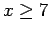 . Then
. Then 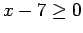 and
and
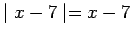 , so that
, so that
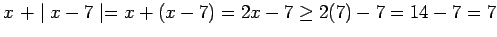 , i.e.,
, i.e.,
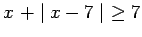 .
.
 : Assume that
: Assume that 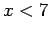 . Then
. Then 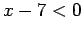 and
and
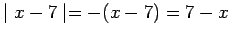 , so that
, so that
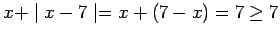 , i.e.,
, i.e.,
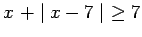 .
.
Thus, for all possible cases, it has been proven that
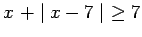 .
.
QED
 : Write clear and complete proofs by cases for each of the following mathematical statements. Find solutions HERE : Page 1 , Page 2 , Page 3 .
: Write clear and complete proofs by cases for each of the following mathematical statements. Find solutions HERE : Page 1 , Page 2 , Page 3 .
- 1. If
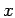 is a real number, then
is a real number, then
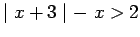 .
.
- 2. If
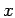 is a real number, then
is a real number, then
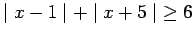 .
.
- 3. The expression
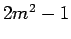 is odd for all integers
is odd for all integers 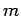 .
.
- 4. If
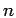 is an even integer, then
is an even integer, then 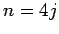 or
or 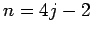 for some integer
for some integer 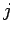 .
.
- 5. If
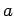 and
and 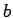 are real numbers, then
are real numbers, then
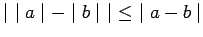 .
.
PROOF BY WORKING BACKWARD
A proof by working backward of a mathematical statement should include the following.
- 1. Begin with a clear written statement of the given facts or assumptions.
- 2. Next provide a clear written statement of what is to be proven.
- 3. Then write the body of the proof. Begin with the final result, which must be PROVEN TRUE, working backward step-by-step, writing equivalent statements, until a connection is made with the assumptions of the problem or some other TRUE statement(s). Provide clear reasoning or substantiation for each step in the proof. A good rule of thumb is this. Treat each proof that you write as a writing exercise as well as a math exercise. Remember that you are trying to convince your reader of the validity of the proof through the clarity and simplicity of your organization and logical reasoning. Finish your proof with a clear statement of that which was to be proven. Shortcuts in proofs are to be avoided at this stage. Writing more details is better for those of you who are just learning how to write proofs.
Here is a simple example of a proof by working backward.
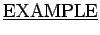 : Prove that
: Prove that
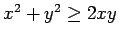 for all real numbers
for all real numbers 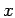 and
and 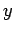 .
.
Proof: ASSUME that 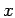 and
and 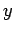 are real numbers. SHOW that
are real numbers. SHOW that
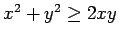 . But
. But
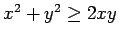 . . . is TRUE
. . . is TRUE
iff
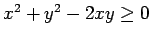 . . . is TRUE
. . . is TRUE
iff
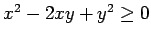 . . . is TRUE
. . . is TRUE
iff
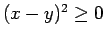 . . . is TRUE .
. . . is TRUE .
Since the last statement is TRUE, all of the equivalent statements are TRUE. In particular,
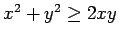 .
.
QED
 : Write clear and complete proofs by working backward for each of the following mathematical statements. Find solutions HERE : Page 1 , Page 2 , Page 3 ,
Page 4 .
: Write clear and complete proofs by working backward for each of the following mathematical statements. Find solutions HERE : Page 1 , Page 2 , Page 3 ,
Page 4 .
- 1. The expression
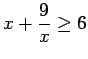 for all real numbers
for all real numbers 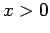 .
.
- 2. If
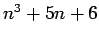 is divisible by 3 for some integer
is divisible by 3 for some integer 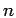 , then
, then
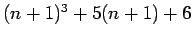 is divisible by 3.
is divisible by 3.
- 3. The expression
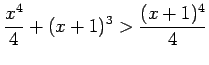 for all real numbers
for all real numbers 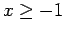 .
.
- 4. There is a fixed positive integer
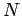 for which
for which
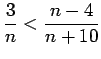 for all integers
for all integers 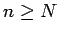 .
.
RETURN to The Proof Page .
Please e-mail your comments, questions, or suggestions to D. A. Kouba at
kouba@math.ucdavis.edu .
Next: About this document ...
Duane Kouba
2002-06-28
![]() :
:
![]() (by assumptions)
(by assumptions)
![]() (by distributive property)
(by distributive property)
![]() ,
,
![]() (by assumptions)
(by assumptions)
![]() (by distributive property)
(by distributive property)
![]() (adding zero)
(adding zero)
![]()
![]() (by commutative property)
(by commutative property)
![]() (by distributive property)
(by distributive property)
![]() ,
,
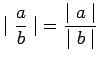 .
.
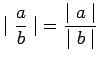 . We will consider the following cases.
. We will consider the following cases.
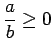 . Then
. Then
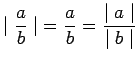 .
.
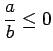 . Then
. Then
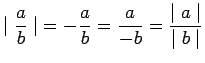 .
.
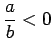 . Then
. Then
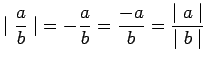 .
.
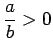 . Then
. Then
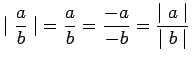 .
.
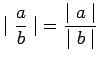 .
.
![]() . . . is TRUE
. . . is TRUE
![]() . . . is TRUE
. . . is TRUE
![]() . . . is TRUE
. . . is TRUE
![]() . . . is TRUE .
. . . is TRUE .
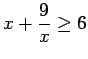 for all real numbers
for all real numbers 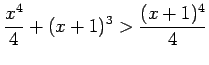 for all real numbers
for all real numbers 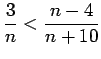 for all integers
for all integers