$polyhedron$

$LattE$

background

Applications to Minkowski's Theorem

Theorem 1 Any convex set (or body) in 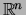${\mathbb{R}}^n$ that has central symmetry and volume greater than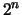

contains an integer lattice point other than $\overline{0}$ .

If is an invertible matrix, then is a linear map. The lattice ${\mathbb{Z}}^n$ is mapped into a system of points in ${\mathbb{R}}^n$ which we call a lattice , where is equal to the determinant of the lattice .

Theorem 2 Let

be any lattice

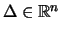of determinant $\Delta\in{\mathbb{R}}^n$ . Then any convex set symmetrical about the origin whose volume is greater than 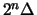$2^n\Delta$ contains a point of

other than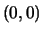

Example 3 Given any real number 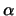$\alpha$ and integer

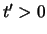, there exists integers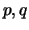

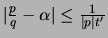such that $\vert\frac{p}{q}-\alpha\vert \leq \frac{1}{\vert p\vert t'}$ .

Take -set parallelogram bounded by the four lines

$\displaystyle y-\alpha x=k, y-\alpha x =-k, x=-t, x=t$

where $t=\vert p\vert t'$ .

$\includegraphics[width=3 in]{para.eps}$

This parallelogram has base , altitude , hence $Area=2t\cdot2k=4tk$ . If we take $k=\frac{1}{t}$ , then . By Minkowski's fundamental theorem, there must be at least one lattice point other than . Thus

$\displaystyle \vert p\vert\leq t$

or,

$\displaystyle \alpha p-k \leq q \leq \alpha p+k.$

Recall $k=\frac{1}{t}$ , so

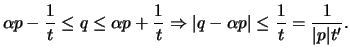
$\displaystyle \alpha p-\frac{1}{t} \leq q \leq \alpha p+\frac{1}{t}\Rightarrow \vert q-\alpha p\vert \leq \frac{1}{t}=\frac{1}{\vert p\vert t'}.$

QED

Example 4 Lagrange: Every positive integer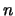

can be expressed as a sum of four squares,

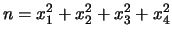$\displaystyle n=x_1^2+x_2^2+x_3^2+x_4^2$

where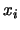

are non-negative integers.

In view of the algebraic identity

$\displaystyle (x_1^2 + x_2^2 + x_3^2 + x_4^2)(y_1^2 + y_2^2 + y_3^2 + y_4^2)$	$\displaystyle =$	$\displaystyle (x_1 y_1 + x_2 y_2 + x_3 y_3 + x_4 y_4)^2$
		$\displaystyle + (x_1 y_2 - x_2 y_1 + x_3 y_4 - x_4 y_3)^2$
		$\displaystyle + (x_1 y_3 - x_2 y_4 - x_3 y_1 + x_4 y_2)^2$
		$\displaystyle + (x_1 y_4 + x_2 y_3 - x_3 y_2 - x_4 y_1)^2,$

we see that

are sums of four squares, thus

is the sum of four squares. Therefore, it is enough to prove the theorem for primes. Let

$\displaystyle A= \left[ \begin{array}{cccc} p & 0 & r & s \\ 0 & p & s & -r \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{array} \right]$

where

are chosen so that $r^2 + s^2 + 1 \equiv 0 \,$ mod $\, p$ . Let $\Lambda=A{\mathbb{Z}}^4$ and suppose that

is a point of $\Lambda$ . If $x\in\Lambda$ , then

$\displaystyle x_1^2 + x_2^2 + x_3^2 + x_4^2$	$\displaystyle =$	$\displaystyle (pt_1 + rt_3 + st_4)^2 + (pt_2 - st_3 - rt_4)^2 + t_3^2 + t_4^2$
	$\displaystyle \equiv$	$\displaystyle (1+r^2+s^2)(t_3^2+t_4^2) \,$ mod $\displaystyle \, p$
	$\displaystyle \equiv$	$\displaystyle 0 \,$ mod $\displaystyle \, p$ .

So we have

. Now consider the ball

$\displaystyle \zeta=\{\overline{x} \, \vert \, x_1^2+x_2^2+x_3^2+x_4^2<2p\}.$

Thus, $\zeta$ is convex and symmetric about 0. A ball of radius $r\in{\mathbb{R}}^4$ has volume $\frac{1}{2}\pi^2 r^4$ . If we take $r=\sqrt{2p}$ , we see

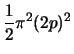$\displaystyle V(\zeta)$	$\displaystyle =$	$\displaystyle \frac{1}{2}\pi^2 (2p)^2$
	$\displaystyle =$	$\displaystyle 2 \pi^2 p^2$
	$\displaystyle >$	$\displaystyle 2^4 p^2$
	$\displaystyle \Rightarrow$	by Minkowski's Fundamental Theorem $\displaystyle \exists \, \overline{x} \in \Lambda, \: \overline{x} \neq 0, \: \overline{x} \in \zeta$
	$\displaystyle \Rightarrow$	$\displaystyle 0<x_1^2+x_2^2+x_3^2+x_4^2<2p$
	$\displaystyle \equiv$	$\displaystyle 0 \,$ mod $\displaystyle \, p,$

so it has to be

QED

Theorem 5 There exists infinitely many positive integers that can be written as a sum of four positive perfect squares, but every integer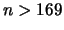

is a sum of five positive perfect squares.

• Mathematics • The University of California, Davis •
• One Shields Avenue • Davis, CA 95616 •