

|
background |
|
|
| Home |
| People |
| Software |
| Theory |
| Background Information |
Minkowski's Theorem
Theorem 1
Let 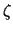 be a convex set in
be a convex set in
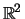 , with
, with 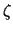 centrally
symmetric and
centrally
symmetric and
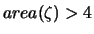 . Then
. Then 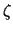 must contain a lattice point
besides
must contain a lattice point
besides 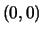 .
.
Definition 2
A set is convex whenever
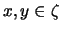 implies
implies
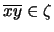 .
.
Definition 3
An object 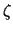 is centrally symmetric if whenever
is centrally symmetric if whenever
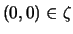 and
and
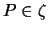 implies
implies
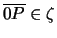 and
and
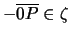 .
.
1. Take
![]()
![\includegraphics[width=2 in]{blob.eps}](img12.png)
2. Assign a copy of ![]() to each lattice point in an
to each lattice point in an ![]() grid.
grid.
![\includegraphics[width=3 in]{nxn.eps}](img15.png)
3. From the above figure we can see
![]() , thus the area covered
by the set s is
, thus the area covered
by the set s is ![]() .
.
4. In fact, all objects cover more (go over a bit). All ![]() objects are
contained in a square of side
objects are
contained in a square of side ![]() , where
, where ![]() is the maximum distance from
the center
is the maximum distance from
the center ![]() to any point of
to any point of ![]() .
.
![\includegraphics[width=2.75 in]{n2s.eps}](img21.png)
5. Now we want to show the inequality
Since
6. Let ![]() be in the intersection of
be in the intersection of
![]() . Then
. Then
![\includegraphics[width=2 in]{overlap.eps}](img37.png)
QED
• Mathematics • The University of California, Davis •
• One Shields Avenue • Davis, CA 95616 •
• One Shields Avenue • Davis, CA 95616 •