

|
background |
|
|
| Home |
| People |
| Software |
| Theory |
| Background Information |
Pick's theorem
Theorem 1
Given a simple closed polygon whose vertices have integer
coordinates, then
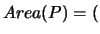 # interior lattice points
# interior lattice points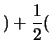 # boundary lattice points
# boundary lattice points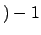
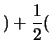 # boundary lattice points
# boundary lattice points
Clearly we can reduce Pick's Theorem to the case of triangles because
![\includegraphics[scale=.75]{A1A2.eps}](img4.png)
where
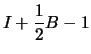 |
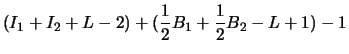 | ||
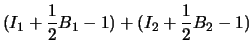 |
We may further assume that there are no other lattice points other than its vertices. Now the idea is to embed the special triangles into rectangles. Thus, all the problem reduces to is to study and show that Pick's theorem is true for
- Rectangles.
- Right angle triangles with integer vertices and no lattice points in the hypotenuse.
For a triangle of case 1
![\includegraphics[scale=.5]{case0.eps}](img19.png)
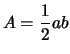 ,
, By thinking of the triangle as a rectangle,
# of interior points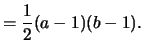
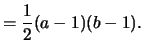
It's crucial that there are no lattice points in the hypotenuse. QED.
Going back to the case of an arbitrary polygon, there is an alogrithm that can be used to count the number of lattice points inside of it:
- Triangulate polygon.
- Count lattice points in each triangle (there are
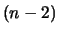 of them). Call this number
of them). Call this number  .
.
- Count lattice points on each diagonal. Call this number
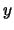 .
.
-
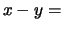 Result
.
Result
.
Definition 2
Let 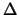 be a triangle whose vertices are integral. We say
be a triangle whose vertices are integral. We say
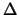 is primitive if it has no other lattice opints in its boundary or interior.
is primitive if it has no other lattice opints in its boundary or interior.
Lemma 3
Every lattice triangle can be divided into primitive triangles.
![\includegraphics[scale=.5]{divprim.eps}](img29.png)
![\includegraphics[scale=.5]{divprim.eps}](img29.png)
Lemma 4
A primitive triangle has area
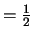 .
.
Lemma 5
Euler's formula: In a triangulation of a polygon,
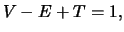
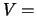 # vertices in primitive triangulation
,
# vertices in primitive triangulation
,
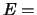 # edge segments in prmitive
triangulation
, and
# edge segments in prmitive
triangulation
, and
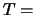 # primitive triangles
.
# primitive triangles
.
where
Corollary 6
The number of primitive triangles from the first lemma is
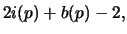
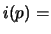 # interior points
and
# interior points
and
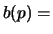 # boundary points
.
# boundary points
.
where
The proof of the third lemma can be done using the corollary and the first lemma:
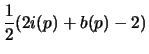 | |||
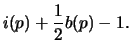 |
The proof of the corollary can be done using the second lemma.
- I wish to write
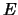 in terms of
in terms of 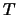
(1) 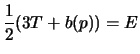
- We have
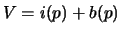 and
and 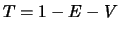
- Substituting equation (1) into the equations from number 2, we get
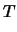
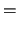
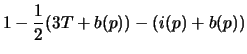
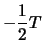
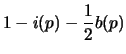
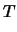
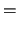
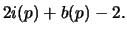
- DONE.
The proof of the second lemma goes as follows:
- Any triangle can be sandwiched into a rectangle with sides parallel to the
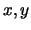 axis.
The proof should be done for all cases, but we will show the hardest case and the
simpler proofs can follow.
axis.
The proof should be done for all cases, but we will show the hardest case and the
simpler proofs can follow.
- From the above picture we get the following equations:
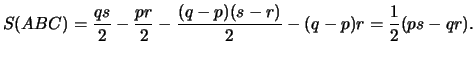
-
- So, if we can show
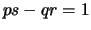 , then we are done.
, then we are done.
- To help us show the above we need to define a new notation
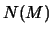
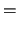
# of lattice points inside but not on the boundary of polygon M 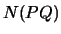
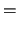
# of lattice points lying on the segment PQ except its ends
- Now we look at two ways to represent
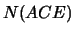 :
:
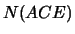
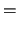
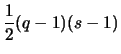
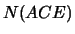
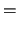
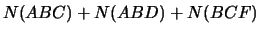
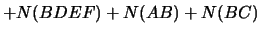
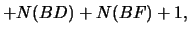
where the ending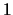 comes from the point
comes from the point 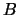 .
.
- Then write the above in terms of
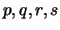 to get
to get
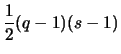
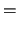
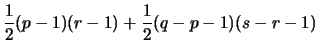
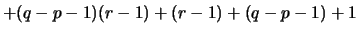
- After simplification we get,
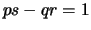
- DONE!
• Mathematics • The University of California, Davis •
• One Shields Avenue • Davis, CA 95616 •
• One Shields Avenue • Davis, CA 95616 •
![\includegraphics[scale=.5]{all4cases.eps}](img18.png)
![\includegraphics[scale=.5]{primtris.eps}](img28.png)
![\includegraphics[scale=.5]{ecase3.eps}](img54.png)