3-dimensional simplex :
In 3 dimensions, we want the expected volume of a random simplex in a simplex S divided by the volume of S, when one of the vertices of the random simplex is fixed at the center of one of the facets of S. As this quantity is affinely invariant, we can assume without loss of generality that S is the convex hull of the canonical basis and the origin.
![]()
![]()
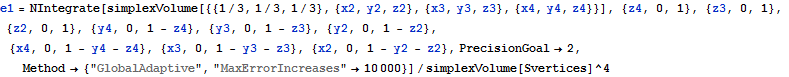

![]()
Same computation, different method:
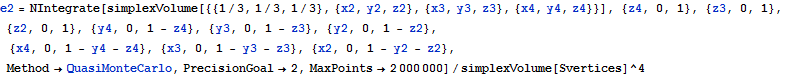
![]()
In 3 dimension, the expected volume of a random simplex in a simplex S divided by the volume of S (from the work of Buchta and Reitzner)
![]()
![]()
The fact that e3> e1 with the results of the paper (the dimension-dependent condition) suggest that the monotonicity under inclusion of the expected volume of a random simplex does not hold in 3 dimensions.