Trigonometry: Double-Angle and Half-Angle Formulas
Double-Angle Formulas
![]()
![]() 2 mm
2 mm
![]() 2 mm
2 mm
![]()
Half-Angle Formulas
![]() , so
, so
![]() , so
, so
Ex 1 Find ![]() using a half-angle formula.
using a half-angle formula.
Sol

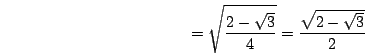
Ex 2 Find ![]() if
if
![]() and
and ![]() is in
Quadrant II.
is in
Quadrant II.
Sol We have that
![]() ,
so
,
so
![]() since
since ![]() in Quadrant II. Therefore
in Quadrant II. Therefore
![]() .
.
Pr A Simplify the expression
![]() .
.
Pr 1 Find ![]() if
if
![]() .
.
Pr 2 Find ![]() if
if
![]() and
and ![]() .
.
Pr 3 Use a half-angle formula to find
![]() .
.
Pr 4 Simplify the expression
![]()
Pr 5 Use half-angle formulas to rewrite
![]() without using powers of trig functions.
without using powers of trig functions.
Pr 6 Use half-angle formulas to rewrite ![]() without using
powers of trig functions.
without using
powers of trig functions.
Pr 7 Find ![]() if
if
![]() and
and
![]() .
.
Pr 8 Find
![]() if
if
![]() and
and
![]() .
.