Graphing Rational Functions
Sol 1
1) Since ![]() is a non-constant polynomial, there are no asymptotes for its graph.
is a non-constant polynomial, there are no asymptotes for its graph.
2) a) ![]() , so the y-intercept is 9.
, so the y-intercept is 9.
b)
![]() , so
, so ![]() iff
iff
![]() or
or ![]() and the x-intercepts are -3,3,-1, and 1.
and the x-intercepts are -3,3,-1, and 1.
3) Using the facts that ![]() and that all the exponents are odd, we get the following
sign chart for
and that all the exponents are odd, we get the following
sign chart for ![]() :
:
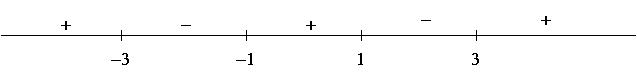
4) Since ![]() ,
, ![]() is an even function and therefore its graph is symmetric around
the y-axis.
is an even function and therefore its graph is symmetric around
the y-axis.
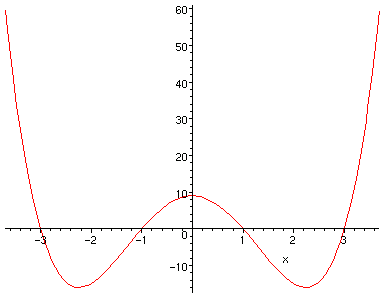
5) Using the above information, we get the following graph:
Sol 2
1) a) The vertical asymptote is the line ![]() .
.
b) Since ![]() and
and ![]() have the same degree and they both have leading coefficient 1,
the horizontal asymptote is the line
have the same degree and they both have leading coefficient 1,
the horizontal asymptote is the line ![]() or
or ![]() .
.
2) a) ![]() , so the y-intercept is -1.
, so the y-intercept is -1.
b)
![]() , so the only x-intercept is -2.
, so the only x-intercept is -2.
3) Using the facts that ![]() and that all the exponents are odd, we get the
following sign chart for
and that all the exponents are odd, we get the
following sign chart for ![]() :
:

4) a) Setting ![]() and solving gives
and solving gives
![]() , so
, so ![]() and
and ![]() .
Therefore there is no solution, so the graph of
.
Therefore there is no solution, so the graph of ![]() does not cross the horizontal asymptote.
does not cross the horizontal asymptote.
b) ![]() is neither even nor odd, so the graph is not symmetric about the y-axis or the origin.
is neither even nor odd, so the graph is not symmetric about the y-axis or the origin.
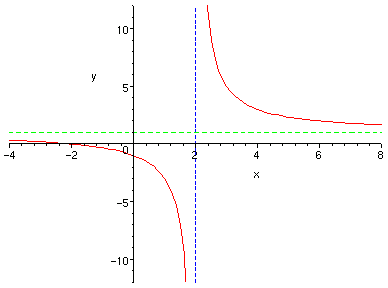
5) Using the information found above, we get the following graph:
Sol 3 [Compare this example to the previous example.]
1) a) Since
![]() for
for ![]() , the only vertical asymptote is the line
, the only vertical asymptote is the line ![]() .
.
b) Since ![]() and
and ![]() have the same degree and they both have leading coefficient 1,
the horizontal asymptote is the line
have the same degree and they both have leading coefficient 1,
the horizontal asymptote is the line ![]() or
or ![]() .
.
2) a) a) ![]() , so the y-intercept is -1.
, so the y-intercept is -1.
b) Since
![]() for
for ![]() ,
,
![]() ; so the only x-intercept is -2.
; so the only x-intercept is -2.
3) Since ![]() and both exponents are odd (and
and both exponents are odd (and ![]() is undefined at -1),
is undefined at -1),
we get the following sign chart for ![]() :
:

4) a) Solving ![]() gives
gives
![]() or
or ![]() or
or ![]() . Since
. Since ![]() is
undefined at -1, though, its graph does not cross the horizontal asymptote.
is
undefined at -1, though, its graph does not cross the horizontal asymptote.
b) ![]() is neither even nor odd, so the graph is not symmetric about the y-axis or the origin.
is neither even nor odd, so the graph is not symmetric about the y-axis or the origin.
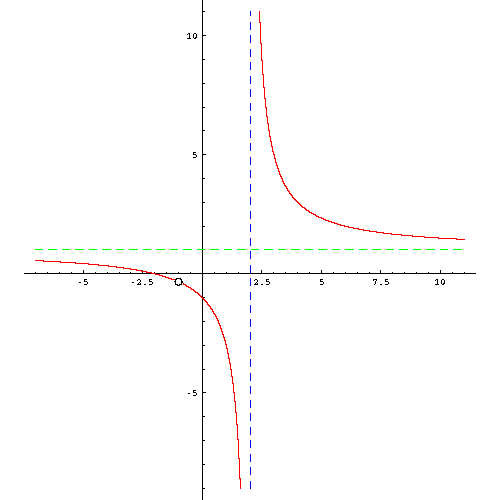
5) Using the above information, we get the graph shown below:
Sol 4
1) a) Since
![]() , the vertical asymptotes are
the lines
, the vertical asymptotes are
the lines ![]() and
and ![]() .
.
b) Since
![]() , the horizontal asymptote is the line
, the horizontal asymptote is the line ![]() (the x-axis).
(the x-axis).
2) a) ![]() , so the y-intercept is 2.
, so the y-intercept is 2.
b)
![]() , so the only x-intercept is 4.
, so the only x-intercept is 4.
3) Since ![]() and all the exponents are odd,
and all the exponents are odd,
we get the following sign chart for ![]() :
:
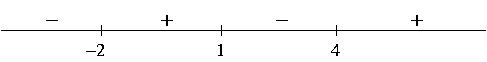
4) a) Setting ![]() and solving gives
and solving gives ![]() , so the graph intersects the horizontal
asymptote at the point
, so the graph intersects the horizontal
asymptote at the point ![]() .
.
b) ![]() is neither even nor odd, so the graph is not symmetric about the y-axis or the origin.
is neither even nor odd, so the graph is not symmetric about the y-axis or the origin.
5) Using the above information, we get the graph shown below:
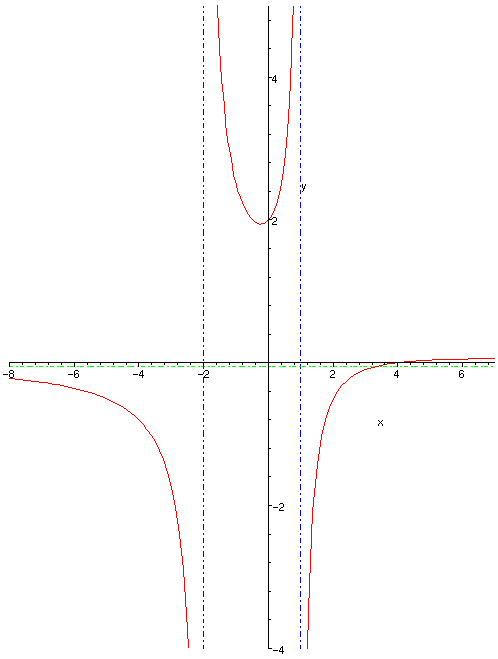
Sol 5
1) a) Since
![]() , the vertical asymptotes are
the lines
, the vertical asymptotes are
the lines ![]() and
and ![]() .
.
b) Since ![]() and
and ![]() have the same degree, the horizontal asymptote is the line
have the same degree, the horizontal asymptote is the line
![]() or
or ![]() .
.
2) a) ![]() , so the y-intercept is 0.
, so the y-intercept is 0.
b)
![]() , so the only x-intercept is 0.
, so the only x-intercept is 0.
3) Using the facts that ![]() and the sign of
and the sign of ![]() changes at 4 and at -4 but does
not change at 0,
changes at 4 and at -4 but does
not change at 0,
we get the following sign chart for ![]() :
:
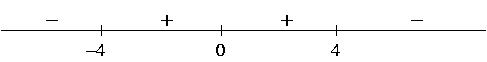
4) a) Setting ![]() gives
gives
![]() , so
, so
![]() and
and ![]() . Therefore there is no solution, so the graph of
. Therefore there is no solution, so the graph of ![]() does not cross its
horizontal asymptote.
does not cross its
horizontal asymptote.
b) Since ![]() ,
, ![]() is an even function and therefore its graph is symmetric about the
y-axis.
is an even function and therefore its graph is symmetric about the
y-axis.
5) Using the information we have found, we get the following graph:
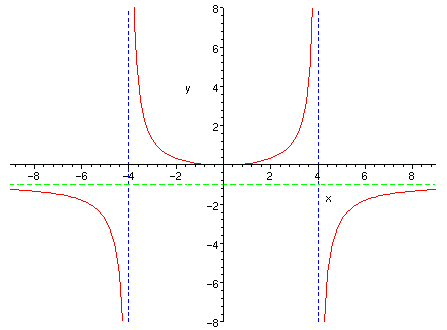
Sol 6
1) a)
![]() , so the only vertical asymptote is
the line
, so the only vertical asymptote is
the line ![]() (the y-axis).
(the y-axis).
b) Since
![]() , there is no horizontal asymptote; but since
, there is no horizontal asymptote; but since
![]() , there is a slanted asymptote:
, there is a slanted asymptote:
Dividing ![]() by
by ![]() gives the original equation
gives the original equation ![]() ,
,
so the line ![]() is the slanted asymptote.
is the slanted asymptote.
2) a) Since ![]() is undefined, there is no y-intercept.
is undefined, there is no y-intercept.
b)
![]() or
or ![]() , so the x-intercepts are 1
and 3.
, so the x-intercepts are 1
and 3.
3) Since
![]() , using the facts that
, using the facts that ![]() and all the
exponents are odd gives the following sign chart for
and all the
exponents are odd gives the following sign chart for ![]() :
:

4) a) Setting ![]() and solving gives
and solving gives ![]() or
or ![]() or
or ![]() . Therefore
there is no solution, so the graph of
. Therefore
there is no solution, so the graph of ![]() does not intersect its slanted asymptote.
does not intersect its slanted asymptote.
b) ![]() is neither even nor odd, so the graph is not symmetric about the y-axis or the origin.
is neither even nor odd, so the graph is not symmetric about the y-axis or the origin.
5) Using the above information, we get the graph shown below:
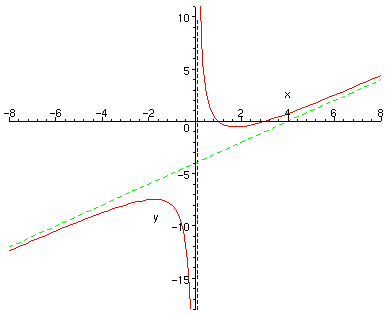
Sol 7
1) a) Since
![]() ,
,
the line ![]() is the only vertical asymptote.
is the only vertical asymptote.
b) Since
![]() , there is no horizontal asymptote; but since
, there is no horizontal asymptote; but since
![]() , there is a slanted asymptote:
, there is a slanted asymptote:
Dividing ![]() by
by ![]() gives the original equation
gives the original equation
![]() ,
,
so the line ![]() is the slanted asymptote.
is the slanted asymptote.
2) a) ![]() , so the y-intercept is -1/2.
, so the y-intercept is -1/2.
b)
![]() , so
, so
![]() ; and therefore the only x-intercept is 1.
; and therefore the only x-intercept is 1.
3) Using the facts that ![]() and the sign of
and the sign of ![]() changes at 2 but does not change
at 1, we get the following sign chart for
changes at 2 but does not change
at 1, we get the following sign chart for ![]() :
:
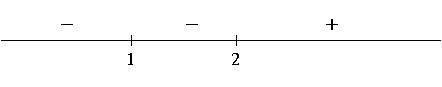
4) a) Setting ![]() and solving gives
and solving gives
![]() , so
, so
![]() and
so
and
so ![]() . Therefore there is no solution, so the graph of
. Therefore there is no solution, so the graph of ![]() does not intersect the slanted
asymptote.
does not intersect the slanted
asymptote.
b) ![]() is neither even nor odd, so the graph is not symmetric about the y-axis or the origin.
is neither even nor odd, so the graph is not symmetric about the y-axis or the origin.
5) Using the above information, we get the graph shown below:
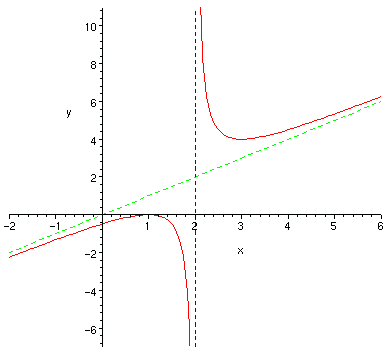
Sol 8
1) a)
![]() , so the only vertical asymptote is
the line
, so the only vertical asymptote is
the line ![]() .
.
b) Since
![]() , there is no horizontal asymptote; but since
, there is no horizontal asymptote; but since
![]() , there is a slanted asymptote:
, there is a slanted asymptote:
Dividing ![]() by
by ![]() gives
gives
![]() , so the line
, so the line
![]() is the slanted asymptote.
is the slanted asymptote.
2) a) ![]() , so the y-intercept is 3.
, so the y-intercept is 3.
b)
![]() or
or ![]() , so the x-intercepts are -2 and 3.
, so the x-intercepts are -2 and 3.
3) Using the facts that ![]() and all the exponents are odd,
and all the exponents are odd,
we get the following sign chart for ![]() :
:
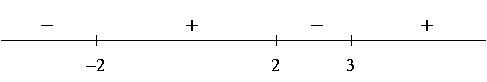
4) a) Setting ![]() gives
gives
![]() , so
, so
![]() and so
and so
![]() . Therefore there is no solution, so the graph of
. Therefore there is no solution, so the graph of ![]() does not intersect the slanted
asymptote.
does not intersect the slanted
asymptote.
b) ![]() is neither even nor odd, so the graph is not symmetric about the y-axis or the origin.
is neither even nor odd, so the graph is not symmetric about the y-axis or the origin.
5) Using the above information, we get the graph shown below:
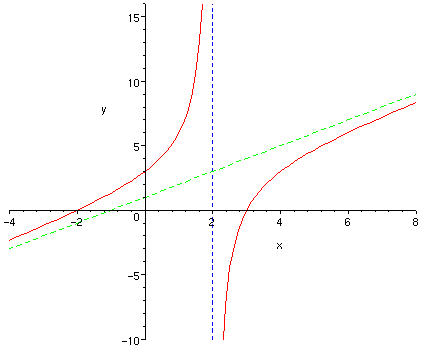
Sol 9
1) a) Since
![]() for
for ![]() , the only vertical asymptote is the line
, the only vertical asymptote is the line ![]() .
.
b) Since ![]() and
and ![]() have the same degree, the horizontal asymptote is given by
have the same degree, the horizontal asymptote is given by
![]() or
or ![]() .
.
2) a) ![]() , so the y-intercept is -1/3.
, so the y-intercept is -1/3.
b)
![]() , so the only x-intercept is -1.
, so the only x-intercept is -1.
3) Since ![]() and both exponents are odd (and
and both exponents are odd (and ![]() is undefined at 1),
is undefined at 1),
we get the following sign chart for ![]() :
:
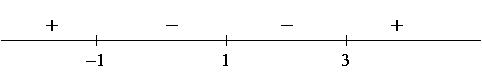
4) a) Setting ![]() gives
gives
![]() , so
, so ![]() and
and ![]() . However,
. However, ![]() is
undefined at 1, so the graph of
is
undefined at 1, so the graph of ![]() does not intersect the horizontal asymptote.
does not intersect the horizontal asymptote.
b) ![]() is neither even nor odd, so the graph is not symmetric about the y-axis or the origin.
is neither even nor odd, so the graph is not symmetric about the y-axis or the origin.
5) From the information above, we get the following graph:
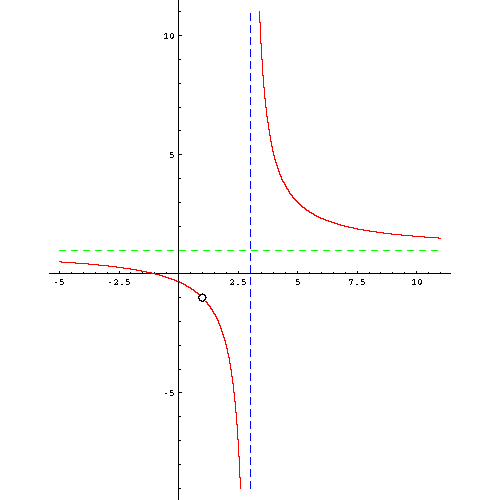
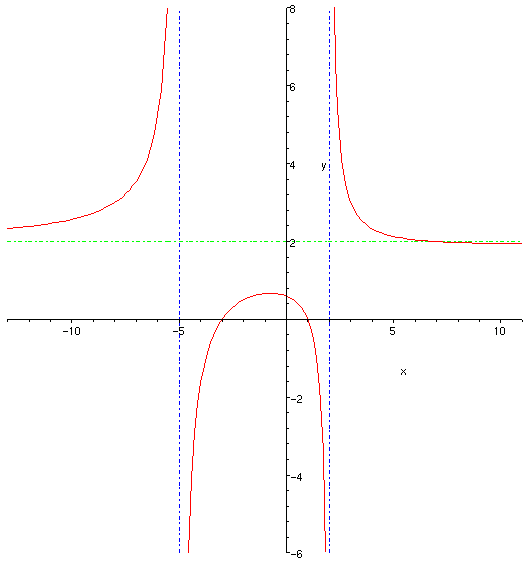
Sol 10
1) a) Since
![]() , the vertical
asymptotes are the lines
, the vertical
asymptotes are the lines ![]() and
and ![]() .
.
b) Since ![]() and
and ![]() have the same degree, the horizontal asymptote is the line
have the same degree, the horizontal asymptote is the line
![]() or
or ![]() .
.
2) a) ![]() , so the y-intercept is 4.
, so the y-intercept is 4.
b)
![]() or
or ![]() , so the x-intercepts are 4 and -2.
, so the x-intercepts are 4 and -2.
3) Using the facts that ![]() and that all the exponents are odd,
and that all the exponents are odd,
we get the following sign chart for ![]() :
:
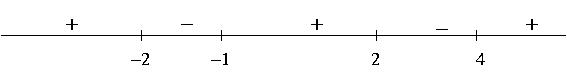
4) a) Setting ![]() gives
gives
![]() , so
, so
![]() gives
gives
![]() or
or ![]() . Therefore the graph of
. Therefore the graph of ![]() crosses the horizontal asymptote at the point
crosses the horizontal asymptote at the point
![]() .
.
b) ![]() is neither even nor odd, so the graph is not symmetric about the y-axis or the origin.
is neither even nor odd, so the graph is not symmetric about the y-axis or the origin.
5) From the information above, we get the following graph:
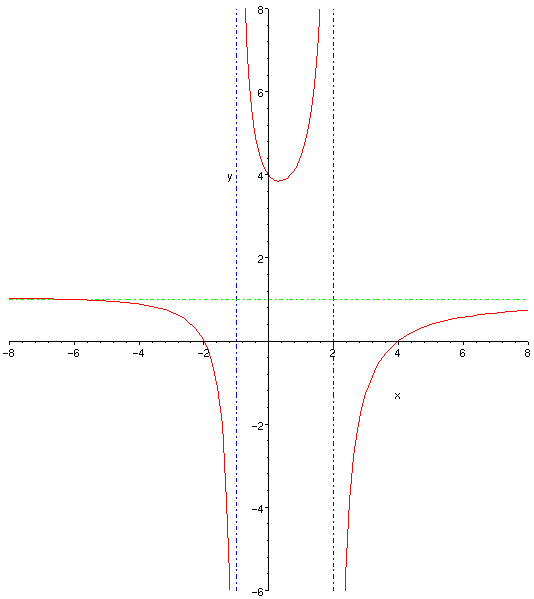
Sol 11
1) a)
![]() , so the vertical
asymptotes are
, so the vertical
asymptotes are ![]() and
and ![]() .
.
b) Since
![]() , there is no horizontal asymptote; but since
, there is no horizontal asymptote; but since
![]() , there is a slanted asymptote:
, there is a slanted asymptote:
Dividing ![]() by
by ![]() gives
gives
![]() ,
,
so the line ![]() is the slanted asymptote.
is the slanted asymptote.
2) a) ![]() , so the y-intercept is 2.
, so the y-intercept is 2.
b)
![]() , so the only x-intercept is 2.
, so the only x-intercept is 2.
3) Using the facts that ![]() and that the sign of
and that the sign of ![]() changes at -1, 2, and 4,
changes at -1, 2, and 4,
we get the following sign chart for ![]() :
:
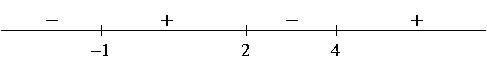
4) a) Setting ![]() gives
gives
![]() , so
, so
![]() and therefore
and therefore ![]() so
so ![]() .
Since
.
Since ![]() , the graph of
, the graph of ![]() intersects the slanted asymptote at the point
intersects the slanted asymptote at the point
![]() .
.
b) ![]() is neither even nor odd, so the graph is not symmetric about the y-axis or the origin.
is neither even nor odd, so the graph is not symmetric about the y-axis or the origin.
5) From the information above, we get the following graph:
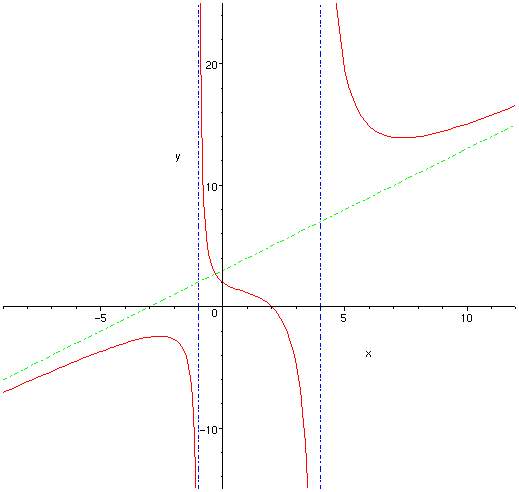
Sol 12
1) a) Since
![]() , the vertical asymptotes are the lines
, the vertical asymptotes are the lines ![]() and
and ![]() .
.
b) Since ![]() and
and ![]() have the same degree, the horizontal asymptote is given by
have the same degree, the horizontal asymptote is given by
![]() or
or ![]() .
.
2) a) ![]() , so the y-intercept is 3/5.
, so the y-intercept is 3/5.
b)
![]() or
or ![]() , so the x-intercepts are -3 and 1.
, so the x-intercepts are -3 and 1.
3) Since ![]() and all the exponents are odd,
and all the exponents are odd,
we get the following sign chart for ![]() :
:
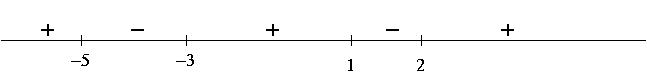
4) a) Setting ![]() gives
gives
![]() , so
, so
![]() and
and ![]() or
or ![]() .
.
Therefore the graph of ![]() intersects the horizontal asymptote at the point
intersects the horizontal asymptote at the point ![]() .
.
b) ![]() is neither even nor odd, so the graph is not symmetric about the y-axis or the origin.
is neither even nor odd, so the graph is not symmetric about the y-axis or the origin.
5) From the information above, we get the following graph:
Return to the Problems for this Topic.
Return to Precalculus Home Page.