Rectangular Coordinates

Sol A The circle has an equation of the form $(x-0)^2+(y-0)^2=r^2$ or $x^2+y^2=r^2$ where $r$ is the distance from $P(5,-3)$ to the origin; so $r=\sqrt{(5-0)^2+(-3-0)^2}=\sqrt{25+9}=\sqrt{34}$ and the circle has the equation $x^2+y^2=34$.

Sol B The midpoint of the line segment AB is given by $M=((4+2)/2,(-1+5)/2)=(3,2)$, so the circle has the equation $(x-3)^2+(y-2)^2=81$.

Sol 1 The midpoint of the line segment AB is given by $M=((5+1)/2,(-2+6)/2)=(3,2)$, so the distance from P to M is equal to $\sqrt{(-3-3)^2+(5-2)^2}=\sqrt{45}=3\sqrt{5}$.

Sol 2 The radius of the circle is the distance from C to the x-axis, so $r=0-(-5)=5$. Therefore the circle has equation $(x-7)^2+(y+5)^2=25$.

Sol 3 The circle has an equation of the form $(x-3)^2+(y-5)^2=r^2$, where the radius $r$ is the distance from C to P. Instead of using the distance formula, though, we can substitute the coordinates of P into the equation to get $(x-3)^2+(y-5)^2=(-2)^2+(-3)^2$ or $(x-3)^2+(y-5)^2=13$.

Sol 4 The radius of the circle is the distance from C to the line $x=3$, so $r=3-(-2)=5$. Therefore the circle has equation $(x+2)^2+(y-4)^2=25$.

Sol 5 The center C of the circle is the midpoint of the line segment between P and Q, so $C=((-2+6)/2,(3+(-1))/2)=(2,1)$. Therefore the circle has an equation of the form $(x-2)^2+(y-1)^2=r^2$, where $r$ is the distance from C to P (or Q). Instead of finding $r$ first, though, we can substitute the coordinates of P into this equation to get $(x-2)^2+(y-1)^2=(-4)^2+2^2$ or $(x-2)^2+(y-1)^2=20$.

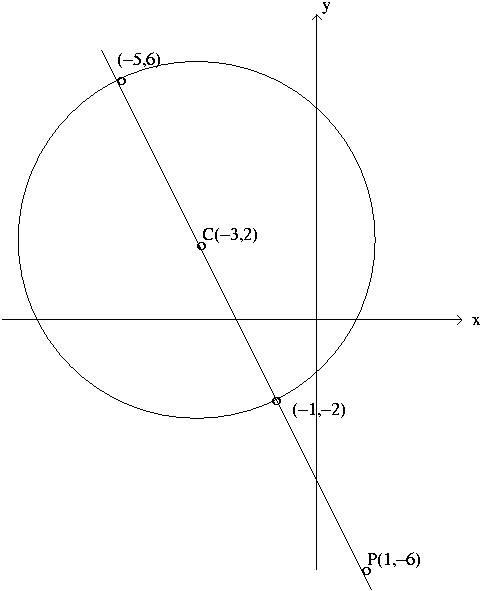
Sol 6 First we can find the center and radius of the circle $x^2-6x+y^2+8y-39=0$ by completing the square: $(x^2-6x+9)+(y^2+8y+16)=39+9+16$ gives $(x-3)^2+(y+4)^2=64$, so the circle has center $C(3,-4)$ and radius $r=8$. The distance from P to C is given by $\sqrt{(8-3)^2+(2-(-4))^2}=\sqrt(25+36)= \sqrt{61}$. Since $\sqrt{61}<8$, the point P is inside the circle.

Sol 7 The center of the circle is the point $C(-3,2)$, and the slope of the line through P and C is given by $m=((-6-2)/1-(-3))=-2$. Therefore the line through P and C has the equation $y-2=-2(x-(-3))$ or $y=-2x-4$, and the point on the circle closest to P will be one of the points of intersection of this line with the circle. Substituting $y=-2x-4$ into the equation of the circle gives $(x+3)^2+(-2x-6)^2=20$, so $x^2+6x+9+4x^2+24x+36=20$ or $5x^2+30x+25=0$. Then $x^2+6x+5=0$, so $(x+5)(x+1)=0$ and $x=-5$ or $x=-1$. Since the x-coordinate of P is 1, the point on the circle closest to P has $x=-1$ and $y=-2(-1)-4=-2$; so it is the point $(-1,-2)$.

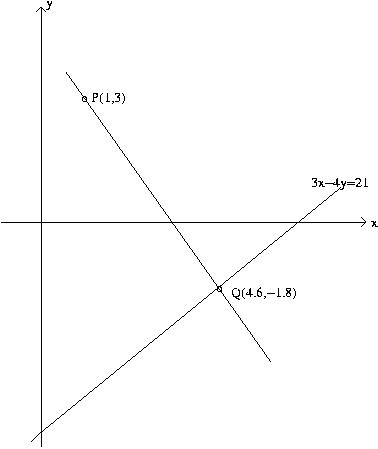
Sol 8 First we will find an equation of the line through P which is perpendicular to the given line. Solving $3x-4y=21$ for $y$ gives $y=3/4x-21/4$, so the given line has slope $m_1=3/4$ and therefore a line perpendicular to this line will have slope $m_2=\frac{-1}{m_1}=-4/3$.

Thus the line through P perpendicular to the given line has equation $y-3=-4/3(x-1)$ or $y=-4/3x+13/3$. These two lines will intersect at a point Q which is the point on the given line closest to P, and we can find the coordinates of Q by substituting $y=-4/3x+13/3$ into the equation $3x-4y=21$ and then solving:

$3x-4(-4/3x+13/3)=21$ gives $3x+16/3x-52/3=21$ or $25/3x=21+52/3=115/3$, so $x=115/25=23/5$ and $y=-4/3(23/5)+13/3=-92/15+65/15=-27/15=-9/5$. Therefore Q is the point $(23/5,-9/5)$,

and the distance from P to the line is the distance from P to Q, which is given by $\sqrt{(1-23/5)^2+(3-(-9/5))^2}= \sqrt{(-18/5)^2+(24/5)^2}=\sqrt{(6/5)^2((-3)^2+4^2)}=(6/5)\sqrt{9+16}= (6/5)\sqrt{25}=(6/5)(5)=6$.

Return to the Problems for this Topic.

Return to Precalculus Home Page.