Solving Polynomial and Rational Inequalities
.
Sol 1 Factoring gives ![]() or
or ![]() . Marking 0,3, and
-2 on a number line, and using that
. Marking 0,3, and
-2 on a number line, and using that
![]() and that all the
exponents are odd, we get the sign chart shown below:
and that all the
exponents are odd, we get the sign chart shown below:

Therefore the solution is given by
![]() .
.
Sol 2 Factoring gives ![]() or
or ![]() .
Marking 0,3, and -2 on a number line, and using that
.
Marking 0,3, and -2 on a number line, and using that
![]() and that the sign changes at 3
and -2 but does not change at 0, we get the sign
chart shown below:
and that the sign changes at 3
and -2 but does not change at 0, we get the sign
chart shown below:

Therefore the solution is given by ![]() .
.
Sol 3 Factoring gives
![]() and that all the exponents are
odd, we get the sign chart shown below:
and that all the exponents are
odd, we get the sign chart shown below:

Since the inequality is not strict, we can include the zeros of the
numerator;
so the solution is given by ![]() .
.
Sol 4 Factoring gives
![]() and that all the exponents are
odd, we get the
sign chart shown below:
and that all the exponents are
odd, we get the
sign chart shown below:
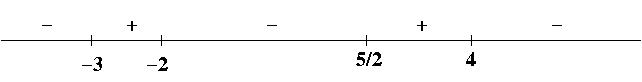
Therefore the solution is given by
![]() .
.
Sol 5 Factoring gives
or
Marking -3,-2,-1,1,2, and 3 on a number line, and using the facts that
![]() and that all the exponents are
odd, we get the following sign chart:
and that all the exponents are
odd, we get the following sign chart:

Since the inequality is not strict, we can include the zeros of the
numerator;
so the solution is given by
![]() .
.
Sol 6 Since ![]() for all
for all ![]() ,
, ![]() and therefore
and therefore ![]() for all
for all ![]() ; so multiplying by
; so multiplying by ![]() gives the equivalent
inequality
gives the equivalent
inequality ![]() .
.
Factoring yields ![]() or
or
![]() ; so marking
; so marking
![]() on a number
line and using that
on a number
line and using that
![]() when
when ![]() and all the
exponents are odd,
we get the following sign chart:
and all the
exponents are odd,
we get the following sign chart:
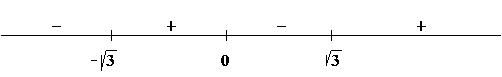
Therefore the solution is given by
![]() .
.
Sol 7 Factoring gives the inequality
Marking off -2,0,1/3,1,3/2, and 4, and using the facts that
![]() and the sign
changes at
3/2,1,-2, and 1/3 and does not change at 0 or at 4, we get the
following sign chart:
and the sign
changes at
3/2,1,-2, and 1/3 and does not change at 0 or at 4, we get the
following sign chart:
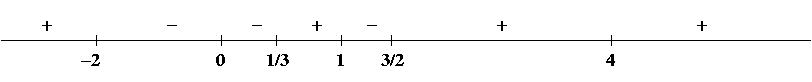
Since the inequality is not strict, we can include the zeros of the
numerator;
so the solution is given by
![]() .
.
Correction: the
solution should include x=0 as well.
Sol 8 Subtracting ![]() from both sides
gives
from both sides
gives ![]() , so
, so ![]() or
or ![]() .
.
Marking -4,0,and 4 on a number line, and using that
![]() and that all the exponents are
odd, we get the following sign chart:
and that all the exponents are
odd, we get the following sign chart:

Therefore ![]() is the solution.
is the solution.
Sol 9 Subtracting ![]() from both sides gives
from both sides gives
Therefore
Marking 2,4, and -1 on a number line, and using the facts that
![]() and that all the exponents are
odd, we get the
following sign chart:
and that all the exponents are
odd, we get the
following sign chart:
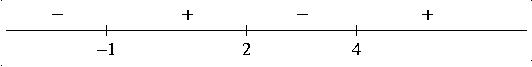
Therefore ![]() is the solution.
is the solution.
Return to the Problems
for this
Topic.
Return to Precalculus Home Page.