Setting Up Functions

In the following problems, we will be asked to set up a function of one variable to describe a certain quantity. In order to do this, we can

1. First set up a function of two variables for the desired quantity, using a picture if applicable.

2. Use the information given in the problem to find an equation relating the two variables in step 1, and then solve for one of the variables in terms of the other.

3. Substitute back into the function found in step 1 to get a function of just one variable.

Ex 1 A rectangle with base $x$ and height $y$ has a perimeter of 120 ft.

Express the area A of the rectangle as a function of $x$.

Sol

1. We know that $A=xy$ for a rectangle.

2. $P=2x+2y=120$, so $x+y=60$ and therefore $y=60-x$.

3. Substituting back gives $A=x(60-x)=60x-x^2$.

Ex 2 A right triangle has base $x$ and height $y$. If the area of the triangle is 5 square inches, express the perimeter of the triangle as a function of $x$.

Sol

1. Using the Pythagorean Theorem, we know that $P=x+y+\sqrt{x^2+y^2}$.

2. Since $A=\frac{1}{2}xy=5$, $xy=10$ and $y=10/x$.

3. Substituting back gives $P=x+\frac{10}{x}+\sqrt{x^2+(10/x)^2}$ $=x+\frac{10}{x}+\sqrt{x^2+100/x^2}$

$=x+\frac{10}{x}+\sqrt{\frac{x^4+100}{x^2}}$ $=x+\frac{10}{x}+\frac{\sqrt{x^4+100}}{x}$ $=x+\frac{10+\sqrt{x^4+100}}{x}$.

Pr 1 A rectangle has base $x$ and height $y$. If the area of the rectangle is 50 square meters, express the perimeter of the rectangle as a function of $y$.

Pr 2 A rectangular pasture has base $x$ and height $y$, and the bottom side of the pasture is bounded by a river. If the other 3 sides of the pasture are bounded by 220 feet of fencing, express the area of the rectangle as a function of $y$.

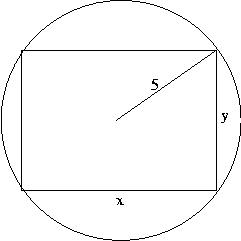
Pr 3 A rectangle with base $x$ and height $y$ is inscribed in a circle of radius 5 inches. Express the area of the rectangle as a function of $x$.

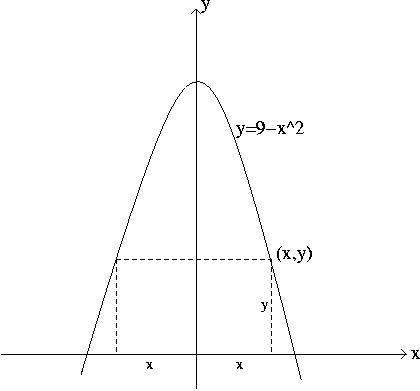
Pr 4 A rectangle has its base on the x-axis and its top two vertices on the graph of $y=9-x^2$. If the top right vertex has coordinates $(x,y)$, Express the area of the rectangle as a function of $x$.

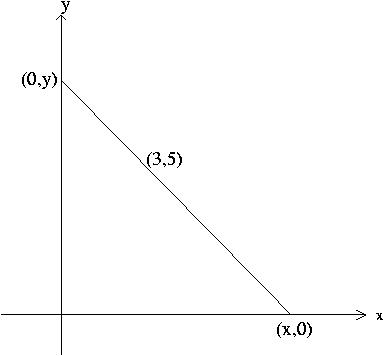
Pr 5 A right triangle has vertices at the origin and at the points $(x,0)$ and $(0,y)$ (with $x$ and $y$ positive). If the hypotenuse of the triangle passes through the point $(3,5)$, express the area of the triangle as a function of $x$.

Pr 6 An athletic field has the shape of a rectangular region with semicircular regions at each end. (See the diagram below.)

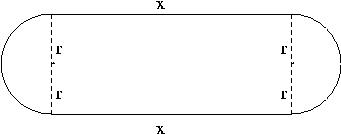
If the perimeter of the field is 400 meters, express the area of the field as a function of the radius $r$ of the semicircles.

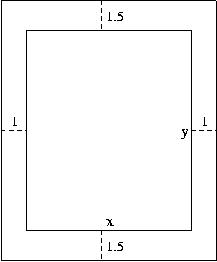
Pr 7 A rectangular page in a book has margins of 1.5 inch at the top and the bottom and 1 inch on the right and the left. If the printed material on the page is a rectangle with base $x$ and height $y$, and its area is 50 square inches, express the area of the page as a function of $x$.

Pr 8 A rectangular box has a square base and a volume of 80 cubic inches. If the side of the base has length $x$ and the height of the box is $h$, express the surface area of the box as a function of $x$.

Pr 9 A rectangular box has a square base and a volume of 60 cubic inches. If the side of the base has length $x$ and the height of the box is $h$, and the material for the top and bottom costs 10 cents per square inch and the material for the other four sides costs 8 cents per square inch, express the cost of the box as a function of $x$.

Pr 10 A right circular cylinder with height $h$ and base radius $r$ has a volume of $60\pi$ cubic inches. Express the total surface area of the cylinder as a function of $r$. (Recall that the area of the side of the cylinder is given by $s=2\pi rh$.)

Pr 11 A right circular cylinder with height $h$ and base radius $r$ has a volume of $54\pi$ cubic inches. If the material for the top and the bottom of the cylinder costs 12 cents per square inch, and the material for the side of the cylinder costs 9 cents per square inch, express the cost of the cylinder as a function of $r$.

Pr 12 A right circular cylinder with height $h$ and base radius $r$ has a total surface area of $80\pi$ square inches. Express the volume of the cylinder as a function of r.

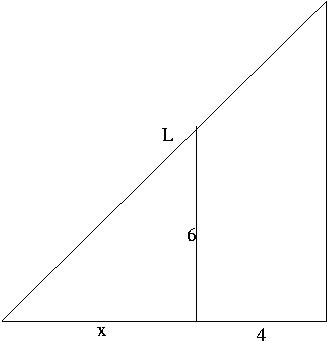
Pr 13 A ladder reaches over a fence 6 feet high to a wall 4 feet behind the fence. Express the length of the ladder as a function of the distance $x$ from the base of the ladder to the fence.

Pr 14 A hiker in the desert is 4 miles from a straight road, and he wants to walk to a town 10 miles down the road from the point on the road closest to him. (See the diagram below.)

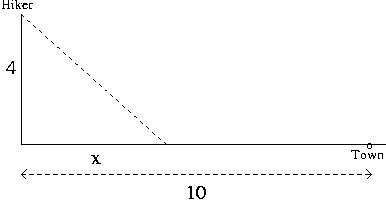
If he can walk 5 mph along the road and 3 mph off the road, express the time it will take him to reach the town as a function of the distance $x$.

Go to Solutions.

Return to Precalculus Home Page.