Welcome to Qinglan Xia's Homepage






Professor Email: qlxia@math.ucdavis.edu
Department of Mathematics Tel. (530)754-0493 (O)
University of California at Davis  Fax: (530)752-6635


My Research  
  • Research Interests: 
    • Geometric measure theory and its applications
    • Optimal transportation and its applications in e.g. mathematical biology, mathematical economics.
  • Publications 

  1. Ramified optimal transportation with payoff on the boundary (With Shaofeng Xu). https://arxiv.org/pdf/2009.07812
  2. The existence of minimizers for an isoperimetric problem with Wasserstein penalty term in unbounded domains (With Bohan Zhou). Advances in Calculus of Variations, vol. , no. , 2021, pp. 000010151520200083. https://doi.org/10.1515/acv-2020-0083
  3. On the Curvature of Metric Triples. https://arxiv.org/pdf/2109.01602.pdf
  4. A fractal shape optimization problem in branched transport (With Paul Pegon, Filippo Santambrogio). Journal de Mathématiques Pures et Appliquées (2018) https://doi.org/10.1016/j.matpur.2018.06.007
  5. Generalized Moran sets generated by step-wise adjustable iterated function systems (With Tynan Lazarus). https://arxiv.org/pdf/1707.08634.pdf
  6. Motivations, ideas, and applications of ramified optimal transportation. ESAIM: Mathematical Modelling and Numerical Analysis. Volume 49, Number 6, November-December 2015. Special Issue - Optimal Transport. pp 1791 - 1832.
  7. Human Placentas, Optimal Transportation and High-risk Autism Pregnancies. (With Carolyn Salafia, etc.). Journal of Coupled Systems and Multiscale Dynamics. 4(4), 260-270. (2016)
  8. Transport efficiency of the human placenta. (With Carolyn Salafia). Journal of Coupled Systems and Multiscale Dynamics. 2, 1-8 (2014)
  9. Optimal transport and placental function. (With Carolyn Salafia and Simon Morgan). The proccedings of the AMMCS 2013 conference.

  10. On landscape functions associated with transport paths. Discrete and Continuous Dynamical Systems - Series A, Vol. 34, No. 4, (2014).

  11. On the ramified optimal allocation problem. (With Shaofeng Xu). arXiv:1103.0571v1, Networks and Heterogeneous Media p591 - 624, Volume 8, Issue 2, June 2013.

  12. The exchange value embedded in a transport system. (With Shaofeng Xu). Applied Mathematics and Optimization. Vol. 62, Issue 2 (2010), 229 - 252. 
         Optimal allocation
  1. Ramified optimal transportation in geodesic metric spaces.     Adv. Calc. Var.
    2. Volume 4, Issue 3, Pages 277–307 (2011)

  2. On the transport dimension of measures. (With Anna Vershynina). SIAM J. MATH. ANAL. Vol. 41, No. 6,(2010) pp. 2407-2430.

  3. Boundary regularity of optimal transport paths.  Adv. Calc. Var. Volume 4, Issue 2, (2011), 153–174

  1. Diffusion-limited aggregation driven by optimal transportation. (With Douglas Unger). Fractals. Vol. 18, No.2 (2010), 247-253.  

  1. Numerical simulation of optimal transport paths. arXiv:0807.3723. 
  1. The geodesic problem in quasimetric spaces.Journal of Geometric Analysis: Volume 19, Issue2 (2009), Page 452-479

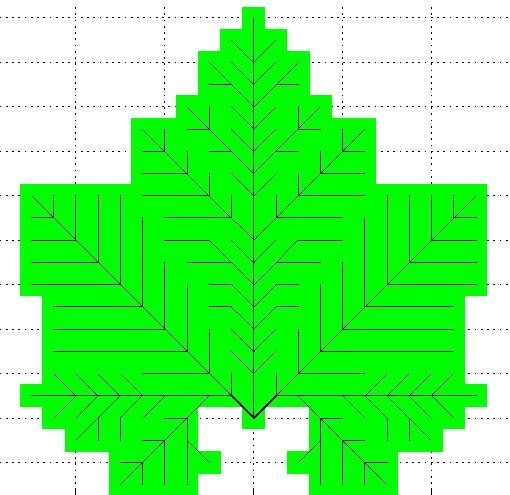
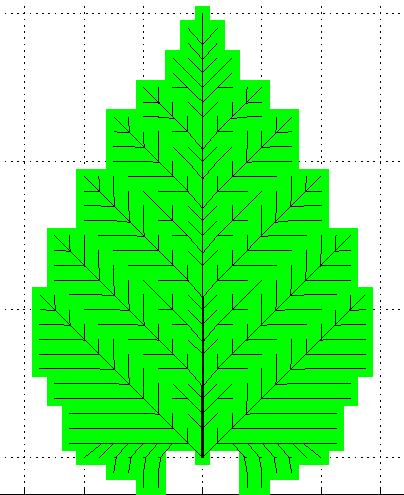
  2. The formation of a tree leaf. ESAIM Control Optim. Calc. Var. 13 (2007), no. 2, 359--377.

  3. An application of optimal transport paths to urban transport networks. Discrete and Continuous Dynmical Systems, Supp. Volume, 2005, 904-910.
  1. Regularity of  minimizers of quasi perimeters with a volume constraint. Interfaces and Free Boundaries. Volume 7, Issue 3, 2005, pp: 339-352

  2. Interior regularity of optimal transport paths.  Calculus of Variations and Partial Differential Equations. Vol. 20, No. 3 (2004) 283-299.

  3. Intersection homology theory via rectifiable currents.  Calculus of Variations and Partial Differential Equations.  Vol. 19, No. 4 (2004), 421-443.
  1. Optimal paths related to transport problems. Communications in Contemporary Mathematics. Vol. 5, No. 2 (2003) 251-279.

  2. Conformal deformation of a closed Riemannian submanifold to a minimal submanifold. (with Xu, Senlin)  Journal of Mathematical Study, Vol 31 (1998), no. 2, 109--115. A summary version is also published on  Chinese Science Bulletin,  Vol 43 (1998), no. 6, 527.

  3. On the spectrum of Clifford hypersurface. (with Xu, Senlin)  Journal of Mathematical Study. Vol 29 (1996), no. 4, 5--9.  
My Teaching 
In Winter 2019, I will teach the course MAT 127B: Real Analysis