Wexler-Raz duality condition

Ignoring fine mathematical details in our explanation one can say that a system of the form $ \gamma_{m,n}= T_{na} M_{mb} \gamma $ is dual to $ g_{m,n}$ if $ f \in \Ltsp(\R)$ has an $ \Ltsp$-convergent representation of the form

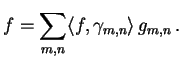$\displaystyle f = \sum_{m,n} \langle f, \gamma_{m,n}\rangle \, g_{m,n}\,.$    

Any function $ \gamma$ generating a dual system $ \gamma_{m,n}$ is called a dual function for $ g$ with respect to the given time-frequency lattice. Among all dual functions the canonical dual obtained via $ \gamma = S^{-1} g$ has least energy. If we want to distinguish it from other duals we denote it by $ \mbox{$^\circ\hspace{-0.5pt}\gamma$}$.

Wexler and Raz have obtained an elegant formulation of the duality condition of the systems $ \{g_{m,n}\}$ and $ \{\gamma_{m,n}\}$. For the case of Gabor analysis over $ \Rst$ their basic result translates into the following characterization of duality with respect to given lattice constants $ a,b$

$\displaystyle \langle \gamma , T_{n/b} M_{m/a} g \rangle = ab\,\, \delta_{n,0}\, \delta_{m,0} \,, \qquad m,n \in \Z\,,$    

i.e., if and only if the two Weyl-Heisenberg systems generated from $ g$ and $ \gamma$ respectively, with respect to the adjoint lattice constant $ 1/b, 1/a$, are biorthogonal to each other.

There are different ways to understand this Wexler-Raz condition , one of them being a beautiful representation of the Gabor frame operator due to Janssen, who has shown that it can be written as a series of time-frequency shifts along the adjoint lattice with parameters $ 1/b, 1/a$. This representation has also been derived at about the same time by Daubechies, H. Landau and E. Landau and by Ron and Shen. It should be noted that the approaches used in these three references are quite different.

Ron and Shen have observed that there is an important duality between between oversampling and undersampling lattices (in a multi-dimensional setting). An $ \Ltsp$-function $ g$ generates a frame for given $ a,b$ if and only if it generates a Riesz basis (for its closed linear span) for the lattice constants $ 1/b, 1/a$.


This survey would be incomplete without mentioning a major tool in the analysis of Gabor systems, namely the Zak-transform. Actually, this transform (in the mathematical community known as the Weil-Brezin transform [Fol89]) has been introduced by Gelfand [Gel50] (1950), and was rediscovered by A. Weil and independently by J. Zak (Zak himself called it the $ kq$-transform). The Zak transform is in fact highly efficient for the case of integer oversampling (i.e., $ 1/ab \in \N$), because in this case it diagonalizes the frame operator. In a generalized form it can also be used to study Gabor expansions for rational oversampling. Recently other techniques (like the Kohn-Nirenberg correspondence or, for numerical purposes, the concept of unitary matrix factorization) have turned out to be powerful tools for the analysis of rationally oversampled Gabor frames.