- PROBLEM 1 : Compute
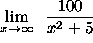 .
.
Click HERE to see a detailed solution to problem 1.
- PROBLEM 2 : Compute
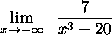 .
.
Click HERE to see a detailed solution to problem 2.
- PROBLEM 3 : Compute
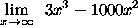 .
.
Click HERE to see a detailed solution to problem 3.
- PROBLEM 4 : Compute
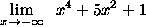 .
.
Click HERE to see a detailed solution to problem 4.
- PROBLEM 5 : Compute
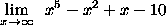 .
.
Click HERE to see a detailed solution to problem 5.
- PROBLEM 6 : Compute
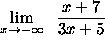 .
.
Click HERE to see a detailed solution to problem 6.
- PROBLEM 7 : Compute
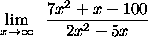 .
.
Click HERE to see a detailed solution to problem 7.
- PROBLEM 8 : Compute
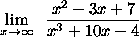 .
.
Click HERE to see a detailed solution to problem 8.
- PROBLEM 9 : Compute
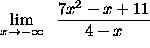 .
.
Click HERE to see a detailed solution to problem 9.
- PROBLEM 10 : Compute
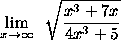 .
.
Click HERE to see a detailed solution to problem 10.
- PROBLEM 11 : Compute
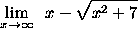 .
.
Click HERE to see a detailed solution to problem 11.
- PROBLEM 12 : Compute
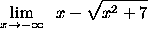 .
.
Click HERE to see a detailed solution to problem 12.
- PROBLEM 13 : Compute
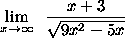 .
.
Click HERE to see a detailed solution to problem 13.
- PROBLEM 14 : Compute
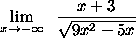 .
.
Click HERE to see a detailed solution to problem 14.
- PROBLEM 15 : Compute
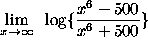 .
.
Click HERE to see a detailed solution to problem 15.
- PROBLEM 16 : Compute limit (x to -infinity) cos [ x/(x^2+10) + pi/3 ] .
Click HERE to see a detailed solution to problem 16.
- PROBLEM 17 : Compute
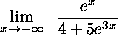 .
.
Click HERE to see a detailed solution to problem 17.
- PROBLEM 18 : Compute
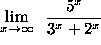 .
.
Click HERE to see a detailed solution to problem 18.
- PROBLEM 19 : Compute
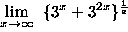 .
.
Click HERE to see a detailed solution to problem 19.