![]() =
= ![]()
(This is true because the expression ![]() approaches
approaches ![]() and the expression x + 3 approaches
and the expression x + 3 approaches ![]() as x approaches
as x approaches
![]() . The next step follows from the following simple fact. If A is a positive quantity, then
. The next step follows from the following simple fact. If A is a positive quantity, then
![]() = A . )
= A . )
= 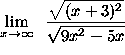
= 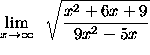
= 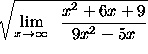
(You will learn later that the previous step is valid because of the continuity of the square root function.)
= 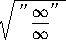
(Inside the square root sign lies an indeterminate form. Circumvent it by dividing each term by ![]() , the highest power of x inside the square root sign.)
, the highest power of x inside the square root sign.)
= 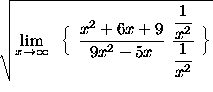
= 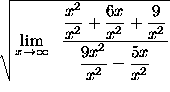
= 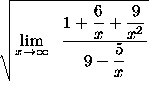
(Each of the three expressions ![]() ,
, ![]() , and
, and
![]() approaches 0 as x approaches
approaches 0 as x approaches ![]() .)
.)
= 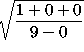
= ![]()
= ![]() .
.
Click HERE to return to the list of problems.
![]() =
= 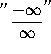
(This is true because the expression ![]() approaches
approaches ![]() and the expression x + 3 approaches
and the expression x + 3 approaches ![]() as x approaches
as x approaches
![]() . The next step follows from the following simple fact. If A is a negative quantity, then
. The next step follows from the following simple fact. If A is a negative quantity, then
![]() = - A so that
= - A so that ![]() = - ( - A ) = A . Please make sure that you think about and understand this before proceeding. )
= - ( - A ) = A . Please make sure that you think about and understand this before proceeding. )
= 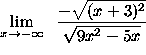
= 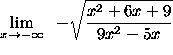
= 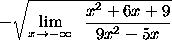
(You will learn later that the previous step is valid because of the continuity of the square root function.)
= 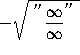
(Inside the square root sign lies an indeterminate form. Circumvent it by dividing each term by ![]() , the highest power of x inside the square root sign.)
, the highest power of x inside the square root sign.)
= 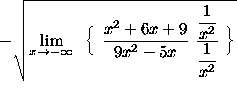
= 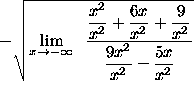
= 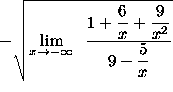
(Each of the three expressions ![]() ,
, ![]() , and
, and
![]() approaches 0 as x approaches
approaches 0 as x approaches ![]() .)
.)
= 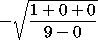
= ![]()
= ![]() .
.
Click HERE to return to the list of problems.
![]() =
= ![]()
(You will learn later that the previous step is valid because of the continuity of the logarithm function. Note also that the expression ![]() leads to the indeterminate form
leads to the indeterminate form ![]() . Circumvent it by dividing each term by
. Circumvent it by dividing each term by ![]() , the highest power of x .)
, the highest power of x .)
= 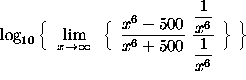
= 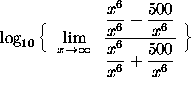
= 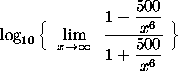
(The term ![]() approaches 0 as x approaches
approaches 0 as x approaches ![]() .)
.)
= ![]()
= ![]()
= 0 .
Click HERE to return to the list of problems.
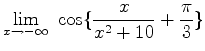 =
= ![]()
(You will learn later that the previous step is valid because of the continuity of the cosine function.)
= ![]()
= ![]()
(The expression ![]() leads to the indeterminate form
leads to the indeterminate form
![]() . Circumvent it by dividing each term by
. Circumvent it by dividing each term by ![]() , the highest power of x in the
expression.)
, the highest power of x in the
expression.)
= 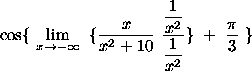
= 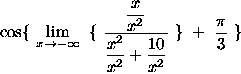
= 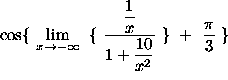
(Each of the terms ![]() and
and ![]() approaches 0 as
x approaches
approaches 0 as
x approaches ![]() .)
.)
= ![]()
= ![]()
= ![]() .
.
Click HERE to return to the list of problems.
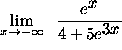
(As x approaches ![]() each of the expressions
each of the expressions ![]() and
and
![]() approaches 0. The following steps explain why.)
approaches 0. The following steps explain why.)
= 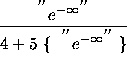
= 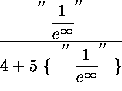
= 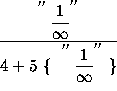
= ![]()
= 0 .
Click HERE to return to the list of problems.
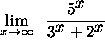 =
= ![]()
(Circumvent this indeterminate form by dividing each term in the expression by
![]() . Division by
. Division by ![]() also works . You might want to try it
both ways to convince yourself of this. Also, BEWARE of making one of the following common MISTAKES :
also works . You might want to try it
both ways to convince yourself of this. Also, BEWARE of making one of the following common MISTAKES :
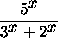 =
= 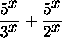 or \
or \
![]() =
= ![]() .)
.)
= 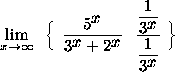
= 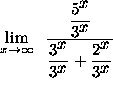
= 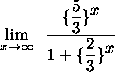
(Since ![]() approaches 0 and
approaches 0 and
![]() approaches
approaches ![]() as x approaches
as x approaches ![]() ,
we get the following resultant limit.)
,
we get the following resultant limit.)
= ![]()
= ![]() .
.
(Thus, the limit does not exist.)
Click HERE to return to the list of problems.
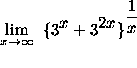 = ``
= `` ![]() ''
truein
truein
(BEWARE of making the following common MISTAKE :
''
truein
truein
(BEWARE of making the following common MISTAKE :
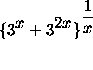 =
= 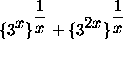 .
Realize also that the form ``
.
Realize also that the form `` ![]() '' is an indeterminate one ! It is not equal to 1 ! Circumvent it in the following
algebraic ways.)
'' is an indeterminate one ! It is not equal to 1 ! Circumvent it in the following
algebraic ways.)
= 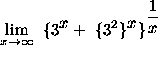
= 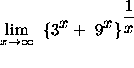
(Factor out the term ![]() . If you have time, try factoring out the term
. If you have time, try factoring out the term ![]() to convince yourself that it DOESN'T seem to help !)
to convince yourself that it DOESN'T seem to help !)
= 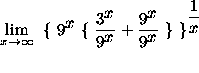
= 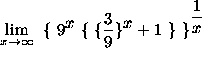
= 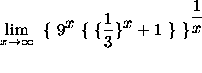
= 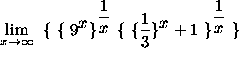
= 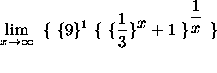
(The expressions ![]() and
and ![]() approach 0 as x approaches
approach 0 as x approaches ![]() .)
.)
= ![]()
= ![]() .
.
= 9 .
Click HERE to return to the list of problems.