![]() .
.
They range in difficulty from easy to somewhat
challenging. If you are going to try these problems before looking at the solutions, you can avoid common mistakes
by making proper use of functional notation and careful use of basic algebra. Keep in mind that the goal (in most cases)
of these types of problems is to be able to divide out the ![]() term so that the indeterminant form
term so that the indeterminant form
![]() of the expression can be circumvented and the limit can be calculated.
of the expression can be circumvented and the limit can be calculated.
![]() .
.
Click HERE to see a detailed solution to problem 1.
![]() .
.
Click HERE to see a detailed solution to problem 2.
![]() .
.
Click HERE to see a detailed solution to problem 3.
![]() .
.
Click HERE to see a detailed solution to problem 4.
![]() .
.
This problem may be more difficult than it first appears.
Click HERE to see a detailed solution to problem 5.
![]() .
.
Click HERE to see a detailed solution to problem 6.
![]() .
.
Click HERE to see a detailed solution to problem 7.
![]() .
.
Click HERE to see a detailed solution to problem 8.
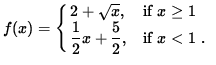
Show that f is differentiable at x=1, i.e., use the limit definition of the derivative to compute f'(1) .
Click HERE to see a detailed solution to problem 9.
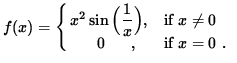
Show that f is differentiable at x=0, i.e., use the limit definition of the derivative to compute f'(0) .
Click HERE to see a detailed solution to problem 10.
f(x) = | x2 - 3x | .
Click HERE to see a detailed solution to problem 11.
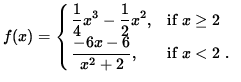
Determine if f is differentiable at x=2, i.e., determine if f'(2) exists.
Click HERE to see a detailed solution to problem 12.
Your comments and suggestions are welcome. Please e-mail any correspondence to Duane Kouba by clicking on the following address :