![]()
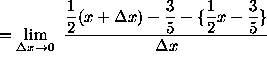
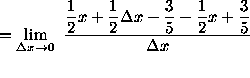
(Algebraically and arithmetically simplify the expression in the numerator.)
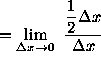
(The term ![]() now divides out and the limit can be calculated.)
now divides out and the limit can be calculated.)
![]()
![]() .
.
Click HERE to return to the list of problems.
![]()
![]()
(Algebraically and arithmetically simplify the expression in the numerator. Please note that there are TWO TYPOS in the numerator of the following quotient. The term "-3x^2+5x" should be "-5x^2+3x". However, steps thereafter are correct.)
![]()
(The remaining steps are correct.)
![]()
(Factor ![]() from the expression in the numerator.)
from the expression in the numerator.)
![]()
(The term ![]() now divides out and the limit can be calculated.)
now divides out and the limit can be calculated.)
![]()
![]() .
.
Click HERE to return to the list of problems.
![]()
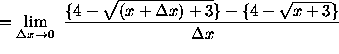
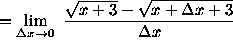
(Eliminate the square root terms in the numerator of the expression by multiplying
by the conjugate of the numerator divided by itself.)
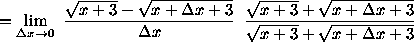
(Recall that ![]() )
)
![]()
![]()
(The term ![]() now divides out and the limit can be calculated.)
now divides out and the limit can be calculated.)
![]()
![]()
![]() .
.
Click HERE to return to the list of problems.
![]()
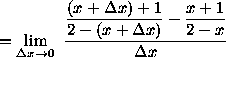
(Get a common denominator for the expression in the numerator. Recall that division by ![]() is the same as
multiplication by
is the same as
multiplication by ![]() . )
. )
![]()
(Algebraically and arithmetically simplify the expression in the numerator. It is important to note that the denominator
of this expression should be left in factored form so that the term ![]() can be easily eliminated later.)
can be easily eliminated later.)
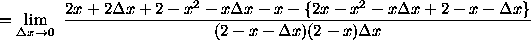
![]()
(The term ![]() now divides out and the limit can be calculated.)
now divides out and the limit can be calculated.)
![]()
![]()
![]() .
.
Click HERE to return to the list of problems.
![]()
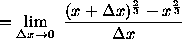
(At this point it may appear that multiplying by the conjugate of the numerator over
itself is a good next step. However, doing something else is a better idea.)
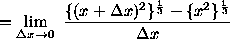
(Note that A - B can be written as the difference of cubes , so that
![]() .
This will help explain the next step.)
.
This will help explain the next step.)
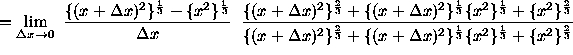
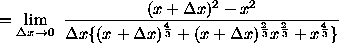
(Algebraically and arithmetically simplify the expression in the numerator.)
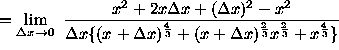
![]()
(The term ![]() now divides out and the limit can be calculated.)
now divides out and the limit can be calculated.)
![]()
![]()
![]()
![]() .
.
Click HERE to return to the list of problems.
![]()
![]()
![]()
(Recall a well-known trigonometry identity :
![]() .)
.)
![]()
![]()
(Recall the following two well-known trigonometry limits :
![]() and
and ![]() .)
.)
![]()
![]()
![]()
![]()
![]() .
.
Click HERE to return to the list of problems.