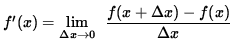
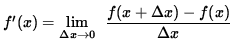
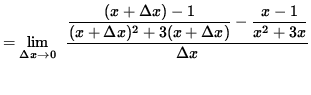
(Get a common denominator for the expression in the numerator. Recall that division by ![]() is the same as multiplication by
is the same as multiplication by
![]() . )
. )
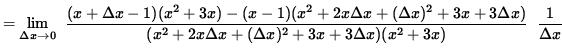
(Algebraically and arithmetically simplify the expression in the numerator. The terms
x3, 2x2, -3x, and
![]() will subtract out. I would show this step, but this web page is not wide enough. It is important to note that the denominator
of this expression should be left in factored form so that the term
will subtract out. I would show this step, but this web page is not wide enough. It is important to note that the denominator
of this expression should be left in factored form so that the term ![]() can be easily eliminated later.)
can be easily eliminated later.)
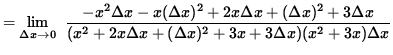
(Factor ![]() from the numerator.)
from the numerator.)
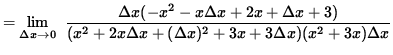
(The term ![]() now divides out and the limit can be calculated.)
now divides out and the limit can be calculated.)
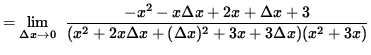
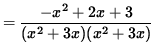
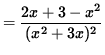 .
.
Click HERE to return to the list of problems.
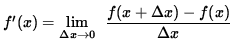
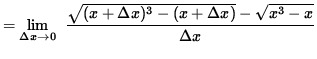
(Eliminate the square root terms in the numerator of the expression by multiplying by the conjugate of the numerator divided by itself.)
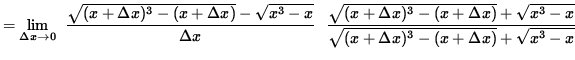
(Algebraically and arithmetically simplify the expression in the numerator. It is important to note that the denominator of this expression should be left in factored form so that the term ![]() can be easily eliminated later.)
can be easily eliminated later.)
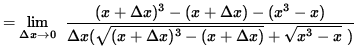
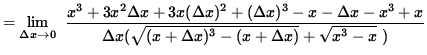
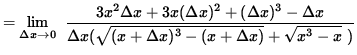
(Factor ![]() from the numerator.)
from the numerator.)
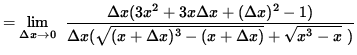
(The term ![]() now divides out and the limit can be calculated.)
now divides out and the limit can be calculated.)
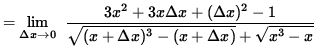
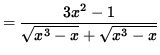
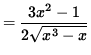 .
.
Click HERE to return to the list of problems.
SOLUTION 9 : The derivative at x=1 is
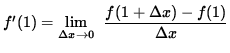
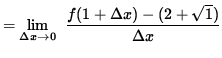
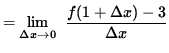 .
.
Note that ![]() can be either positive or negative, and
can be either positive or negative, and
![]() when
when
![]() ,
and
,
and
![]() when
when
![]() . Thus,
. Thus,
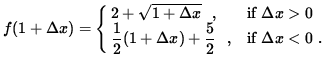
Further work requires the use of one-sided limits. First, the right-hand limit is
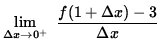 =
=
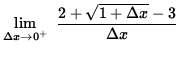
=
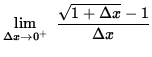
=
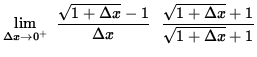
=
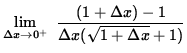
=
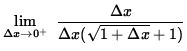
=
![]()
=
![]()
=
![]() .
.
The left-hand limit is
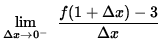 =
=
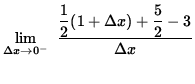
=
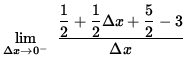
=
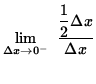
=
![]()
=
![]() .
.
Thus, both one-sided limits exist and are equal, so that f is differentiable at x=1 with
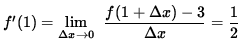 .
.
Click HERE to return to the list of problems.
SOLUTION 10 : The derivative at x=0 is
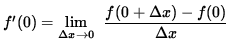
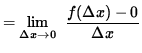
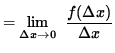
(Note that
![]() .)
.)
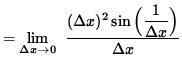
![]() .
.
But for
![]()
![]()
so that
![]() implies that
implies that
![]() .
.
Since
![]() ,
it follows from the Squeeze Principle that
,
it follows from the Squeeze Principle that
![]() .
.
In a similar fashion (Assume that
![]() .) it can easily be shown that
.) it can easily be shown that
![]() .
.
Thus, both one-sided limits exist and are equal, so that function f is differentiable at x=0 with
![]() .
.
REMARK : What follows is a common INCORRECT attempt to solve this problem using another method. Since
![]() for
for ![]() ,
it follows, using the product rule and chain rule, that
,
it follows, using the product rule and chain rule, that
![]()
![]()
for ![]() .
Then
.
Then
![]()
![]() .
.
Because the term
![]() oscillates between 1 and -1 as
oscillates between 1 and -1 as
![]() approaches zero , this limit does not exist. An INCORRECT conclusion would be that f'(0) does not exist, i.e., f is not differentiable at x=0. If f' were continuous at x=0 , this would be a valid method to compute f'(0) .
approaches zero , this limit does not exist. An INCORRECT conclusion would be that f'(0) does not exist, i.e., f is not differentiable at x=0. If f' were continuous at x=0 , this would be a valid method to compute f'(0) .
Click HERE to return to the list of problems.
SOLUTION 11 : First rewrite f(x). That is,
f(x) = | x2 - 3x | = | x(x-3) |
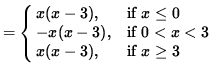
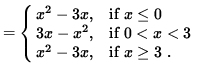
Assume that x < 0. Then
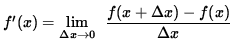
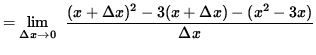
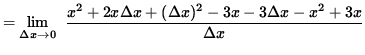
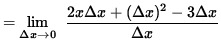
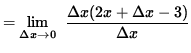
![]()
= 2x - 3 .
Assume that x>3. Then it is also true that f'(x) = 2x - 3. Assume that 0 < x < 3. Then
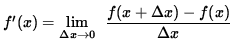
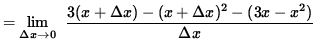
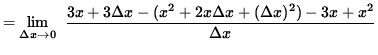
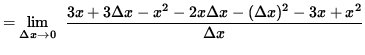
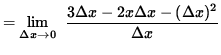
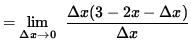
![]()
= 3 - 2x .
Now check for differentiability at x=0, i.e., compute f'(0). Then
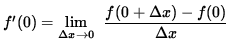
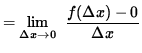
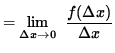 .
.
If
![]() ,
then
,
then
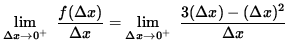
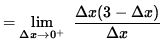
![]()
= 3.
If
![]() ,
then
,
then
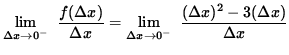
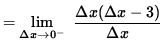
![]()
= - 3.
Since the one-sided limits exist but are NOT EQUAL,
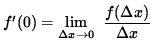 does not exist, and f is not differentiable at x = 0. Now check for differentiability at x=3, i.e., compute f'(3). Then
does not exist, and f is not differentiable at x = 0. Now check for differentiability at x=3, i.e., compute f'(3). Then
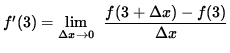
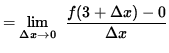
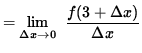 .
.
If
![]() , then
, then
![]() so that
so that
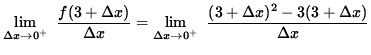
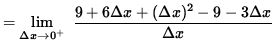
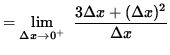
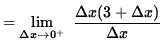
![]()
= 3.
If
![]() , then
, then
![]() so that
so that
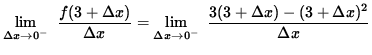
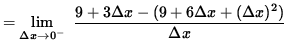
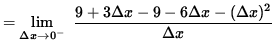
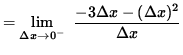
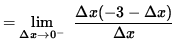
![]()
= - 3.
Since the one-sided limits exist but are NOT EQUAL,
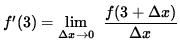 does not exist, and f is not differentiable at x = 3. Summarizing, the derivative of f is
does not exist, and f is not differentiable at x = 3. Summarizing, the derivative of f is
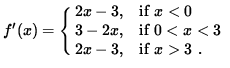
Function f is not differentiable at x=0 or x=3.
Click HERE to return to the list of problems.
SOLUTION 12 :
First, determine if f is continuous at x=2, i.e., determine if
![]() . For x > 2
. For x > 2
![]()
![]()
= 0.
For x < 2
![]()
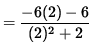
= -3.
Thus, the one-sided limits exist but are NOT EQUAL, so that
![]() does not exist and function f is NOT CONTINUOUS AT x=0 . Since function f is NOT CONTINUOUS AT x=0 , function f is NOT DIFFERENTIABLE at x=2 .
does not exist and function f is NOT CONTINUOUS AT x=0 . Since function f is NOT CONTINUOUS AT x=0 , function f is NOT DIFFERENTIABLE at x=2 .
REMARK 1 : Use of the limit definition of the derivative of f at x=2 also leads to a correct solution to this problem.
REMARK 2 : What follows is a common INCORRECT attempt to solve this problem using another method. For x>2
![]() .
.
For x<2
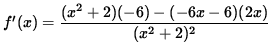
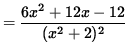 .
.
Then
![]()
![]()
= 1 ,
and
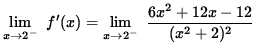
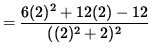
= 1 .
An INCORRECT conclusion would be that f'(2) = 1. If f' were continuous at x=2 , this would be a valid method to compute f'(2) .
Click HERE to return to the list of problems.