GRAPHING OF FUNCTIONS USING FIRST AND SECOND DERIVATIVES
The following problems illustrate detailed graphing of functions of one variable using the first and second derivatives. Problems range in difficulty from average to challenging. If you are going to try these problems before looking at the solutions, you can avoid common mistakes by carefully labeling critical points, intercepts, and inflection points. In addition, it is important to label the distinct sign charts for the first and second derivatives in order to avoid unnecessary confusion of the following well-known facts and definitions.
Here are instruction for establishing sign charts (number line) for the first and second derivatives. To establish a sign chart (number lines) for f' , first set f' equal to zero and then solve for x . Mark these x-values underneath the sign chart, and write a zero above each of these x-values on the sign chart. In addition, mark x-values where the derivative does not exist (is not defined). For example, mark those x-values where division by zero occurs in f' . Above these x-values and the sign chart draw a dotted vertical line to indicate that the value of f' does not exist at this point. These designated x-values establish intervals along the sign chart. Next, pick points between these designated x-values and substitute them into the equation for f' to determine the sign ( + or - ) for each of these intervals. Beneath each designated x-value, write the corresponding y-value which is found by using the original equation y = f(x) . These ordered pairs
(x, y) will be a starting point for the graph of f . This completes the sign chart for f' . Establish a sign chart (number line) for f'' in the exact same manner. To avoid overlooking zeroes in the denominators of f' and f'' , it is helpful to rewrite all negative exponents as positive exponents and then carefully manipulate and simplify the resulting fractions.
FACTS and DEFINITIONS
1. If the first derivative f' is positive (+) , then the function f is increasing (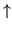 )
.
)
.
2. If the first derivative f' is negative (-) , then the function f is decreasing (
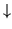 )
.
)
.
3. If the second derivative f'' is positive (+) , then the function f is concave up (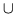 )
.
)
.
4. If the second derivative f'' is negative (-) , then the function f is concave down (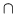 )
.
)
.
5. The point x=a determines a relative maximum for function f if f is continuous at x=a , and the first derivative f' is positive (+) for x<a and negative (-) for x>a . The point x=a determines an absolute maximum for function f if it corresponds to the largest y-value in the range of f .
6. The point x=a determines a relative minimum for function f if f is continuous at x=a , and the first derivative f' is negative (-) for x<a and positive (+) for x>a . The point x=a determines an absolute minimum for function f if it corresponds to the smallest y-value in the range of f .
7. The point x=a determines an inflection point for function f if f is continuous at x=a , and the second derivative f'' is negative (-) for x<a and positive (+) for x>a , or if f'' is positive (+) for x<a and negative (-) for x>a .
8. THE SECOND DERIVATIVE TEST FOR EXTREMA (This can be used in place of statements 5. and 6.) : Assume that y=f(x) is a twice-differentiable function with f'(c)=0 .
a.) If f''(c)<0 then f has a relative maximum value at x=c .
b.) If f''(c)>0 then f has a relative minimum value at x=c .
These are the directions for problems 1 through 10. For each function state the domain. Determine all relative and absolute maximum and minimum values and inflection points. State clearly the intervals on which the function is increasing (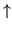 )
, decreasing (
)
, decreasing (
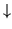 )
, concave up (
)
, concave up (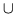 )
, and concave down (
)
, and concave down (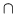 )
. Determine x- and y-intercepts and vertical and horizontal asymptotes when appropriate. Neatly sketch the graph.
)
. Determine x- and y-intercepts and vertical and horizontal asymptotes when appropriate. Neatly sketch the graph.
- PROBLEM 1 : Do detailed graphing for
f(x) = x3 - 3x2 .
Click HERE to see a detailed solution to problem 1.
- PROBLEM 2 : Do detailed graphing for
f(x) = x4 - 4x3 .
Click HERE to see a detailed solution to problem 2.
- PROBLEM 3 : Do detailed graphing for
f(x) = x3 (x-2)2 .
Click HERE to see a detailed solution to problem 3.
- PROBLEM 4 : Do detailed graphing for
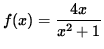 .
.
Click HERE to see a detailed solution to problem 4.
- PROBLEM 5 : Do detailed graphing for
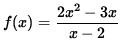 .
.
Click HERE to see a detailed solution to problem 5.
- PROBLEM 6 : Do detailed graphing for
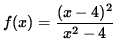 .
.
Click HERE to see a detailed solution to problem 6.
- PROBLEM 7 : Do detailed graphing for
f(x) = x - 3x1/3 .
Click HERE to see a detailed solution to problem 7.
- PROBLEM 8 : Do detailed graphing for
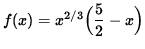 .
.
Click HERE to see a detailed solution to problem 8.
- PROBLEM 9 : Do detailed graphing for
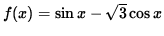 for x in
for x in
![$ [0, 2\pi ] $](img10.gif) .
.
Click HERE to see a detailed solution to problem 9.
- PROBLEM 10 : Do detailed graphing for
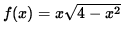 .
.
Click HERE to see a detailed solution to problem 10.
- PROBLEM 11 : Consider the cubic polynomial
y = A x3 + 6x2 - Bx , where A and B are unknown constants. If possible, determine the values of A and B so that the graph of y has a maximum value at x= -1 and an inflection point at x=1 .
Click HERE to see a detailed solution to problem 11.
Click HERE to return to the original list of various types of calculus problems.
Your comments and suggestions are welcome. Please e-mail any correspondence to Duane Kouba by
clicking on the following address :
kouba@math.ucdavis.edu
Duane Kouba
1998-06-03
![]() )
.
)
.
![]() )
.
)
.
![]() )
.
)
.
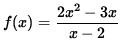 .
.
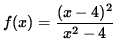 .
.