SOLUTION 7 : The domain of f is all x-values. Now determine a sign chart for the first derivative, f' . Then
f'(x) = 1 - 3 (1/3) x1/3-1
= 1 - x-2/3
![]()
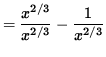
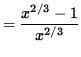
= 0
when
x2/3 - 1 = 0 . Thus,
x2/3 = 1 so that
![]() and
x = 1 or x = -1 . In addition, note that f' is NOT DEFINED at x=0 . To avoid using a calculator, it is convenient to use numbers like
x= -8, -1/8, 1/8, and 8 as "test points" to construct the adjoining sign chart for the first derivative, f' .
and
x = 1 or x = -1 . In addition, note that f' is NOT DEFINED at x=0 . To avoid using a calculator, it is convenient to use numbers like
x= -8, -1/8, 1/8, and 8 as "test points" to construct the adjoining sign chart for the first derivative, f' .
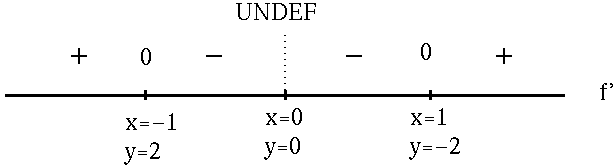
Now determine a sign chart for the second derivative, f'' . Beginning with
f'(x)= 1 - x-2/3 ,
we get
f''(x)= 0 - (-2/3) x-2/3 - 1
= (2/3) x-5/3
![]()
= 0
for NO x-values . However, note that f'' is NOT DEFINED at x=0 . To avoid using a calculator, it is convenient to use numbers like x= -1 and x=1 as "test points" to construct the adjoining sign chart for the second derivative, f'' .
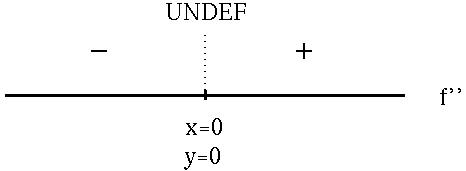
Now summarize the information from each sign chart.
FROM f' :
f is (![]() )
for x<-1 and x>1 ;
)
for x<-1 and x>1 ;
f is (
![]() )
for -1<x<0 and 0<x<1 ;
)
for -1<x<0 and 0<x<1 ;
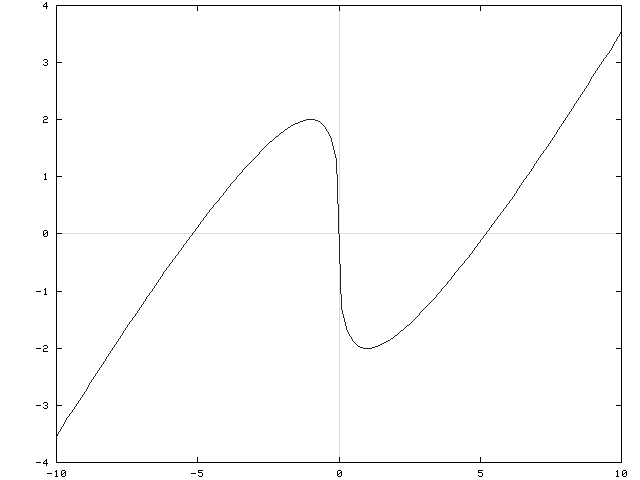
f has a relative maximum at x=-1 , y=2 ;
f has a relative minimum at x=1 , y=-2 .
FROM f'' :
f is (![]() )
for x>0 ;
)
for x>0 ;
f is (![]() )
for x<0 ;
)
for x<0 ;
f has an inflection point at x=0 , y=0 .
OTHER INFORMATION ABOUT f :
If x=0 , then y=0 so that y=0 is the y-intercept. If y=0 , then
x - 3x1/3 = x1/3 ( x2/3 - 3 ) = 0 so that x1/3=0 or
x2/3 = 3 . Thus,
![]() or
or
![]() , so that
, so that
![]() and x=0 are the x-intercepts. There are no horizontal or vertical asymptotes. See the adjoining detailed graph of f .
and x=0 are the x-intercepts. There are no horizontal or vertical asymptotes. See the adjoining detailed graph of f .
Click HERE to return to the list of problems.
SOLUTION 8 : The domain of f is all x-values. Now determine a sign chart for the first derivative, f' . Beginning with
![]()
= (5/2)x2/3 - x2/3 x1
= (5/2)x2/3 - x2/3+1
= (5/2)x2/3 - x5/3
we get
f'(x) = (5/2)(2/3)x2/3-1 - (5/3)x5/3-1
= (5/3) x-1/3 - (5/3)x2/3
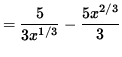
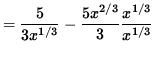
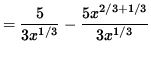
![]()
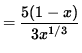
= 0
when x=1 . In addition, note that f' is NOT DEFINED at x=0 . See the adjoining sign chart for the first derivative, f' .
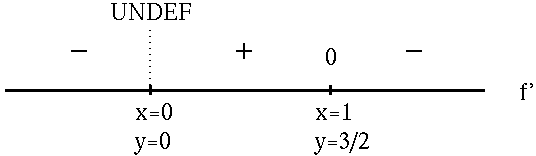
Now determine a sign chart for the second derivative, f'' . Beginning with
f'(x)= (5/3)x-1/3 - (5/3) x2/3 ,
we get
f''(x)= (5/3)(-1/3) x-1/3-1 - (5/3)(2/3) x2/3-1
= (-5/9) x-4/3 - (10/9) x-1/3
![]()
![]()
![]()
![]()
![]()
![]()
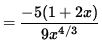
= 0
when 1+2x=0 or x= -1/2 . In addition, note that f'' is NOT DEFINED at x=0 . See the adjoining sign chart for the second derivative, f'' .
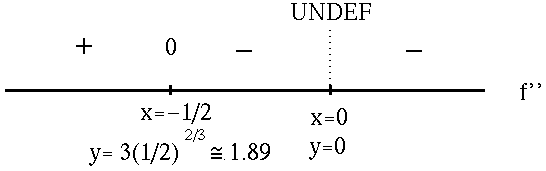
Now summarize the information from each sign chart.
FROM f' :
f is (![]() )
for 0<x<1 ;
)
for 0<x<1 ;
f is (
![]() )
for x<0 and x>1 ;
)
for x<0 and x>1 ;
f has a relative maximum at x=1 , y= 3/2 ;
f has a relative minimum at x=0 , y=0 .
FROM f'' :
f is (![]() )
for x< -1/2 ;
)
for x< -1/2 ;
f is (![]() )
for -1/2<x<0 and x>0 ;
)
for -1/2<x<0 and x>0 ;
f has an inflection point at x=-1/2 ,
![]() .
.
OTHER INFORMATION ABOUT f :
If x=0 , then y=0 so that y=0 is the y-intercept. If y=0 , then
x2/3 ( 5/2 - x ) = 0 so that x2/3=0 or
5/2 - x = 0 . Thus, x=0 and x = 5/2 are the x-intercepts. There are no horizontal or vertical asymptotes. See the adjoining detailed graph of f .
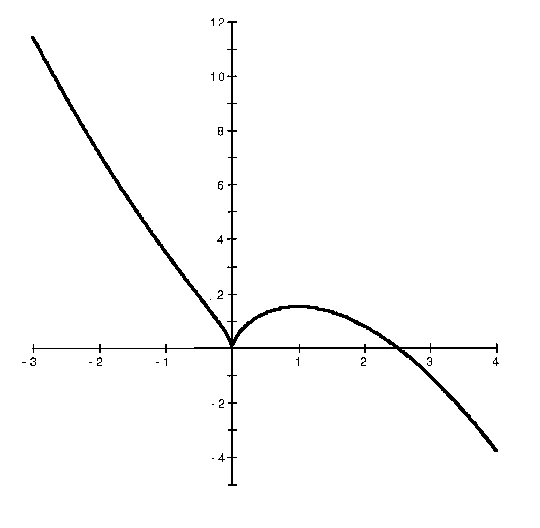
Click HERE to return to the list of problems.
SOLUTION 9 :
The domain of f is artificially restricted to be
![]() . Now determine a sign chart for the first derivative, f' . Begin with
. Now determine a sign chart for the first derivative, f' . Begin with
![]()
![]()
= 0 .
Then
![]()
so that
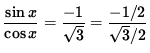
or
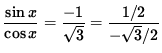 .
.
A well-known angle x in the second quadrant with
![]() and
and
![]()
is ![]() . A well-known angle x in the fourth quadrant with
. A well-known angle x in the fourth quadrant with
![]() and
and
![]()
is
![]() . It is convenient to use
. It is convenient to use
![]() and
and ![]() as test points in the first derivative
as test points in the first derivative
![]() when constructing the adjoining sign chart for the first derivative, f' .
when constructing the adjoining sign chart for the first derivative, f' .
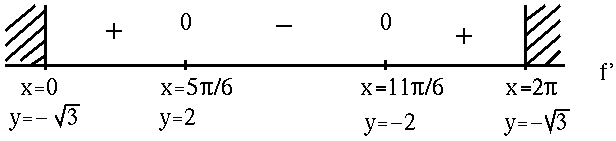
Now determine a sign chart for the second derivative, f'' . Begin with
![]()
= 0 .
Then
![]()
so that
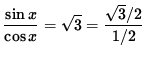
or
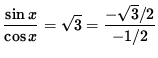 .
.
A well-known angle x in the first quadrant with
![]() and
and
![]()
is ![]() . A well-known angle x in the third quadrant with
. A well-known angle x in the third quadrant with
![]() and
and
![]()
is ![]() . It is convenient to use
. It is convenient to use ![]() and
and ![]() as test points in the second derivative
as test points in the second derivative
![]() when constructing the adjoining sign chart for the second derivative, f'' .
when constructing the adjoining sign chart for the second derivative, f'' .
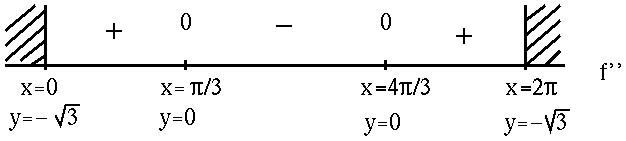
Now summarize the information from each sign chart.
FROM f' :
f is (![]() )
for
)
for
![]() and
and
![]() ;
;
f is (
![]() )
for
)
for
![]() ;
;
f has a relative maximum at ![]() ,
,
![]() ;
;
f has an absolute maximum at ![]() , y= 2 ;
, y= 2 ;
f has a relative minimum at x=0 ,
![]()
f has an absolute minimum at ![]() , y=-2 .
, y=-2 .
FROM f'' :
f is (![]() )
for
)
for ![]() and
and
![]() ;
;
f is (![]() )
for
)
for
![]() ;
;
f has inflection points at ![]() , y=0 and
, y=0 and ![]() , y=0 .
, y=0 .
OTHER INFORMATION ABOUT f :
If x=0 , then
![]() , so that
, so that
![]() is the y-intercept. If y=0 , then
is the y-intercept. If y=0 , then
![]() and
and
![]() (This is the same equation used to solve f''(x)=0 .) so that
(This is the same equation used to solve f''(x)=0 .) so that ![]() and
and
![]() are the y-intercepts. There are no horizontal or vertical asymptotes. See the adjoining detailed graph of f .
are the y-intercepts. There are no horizontal or vertical asymptotes. See the adjoining detailed graph of f .
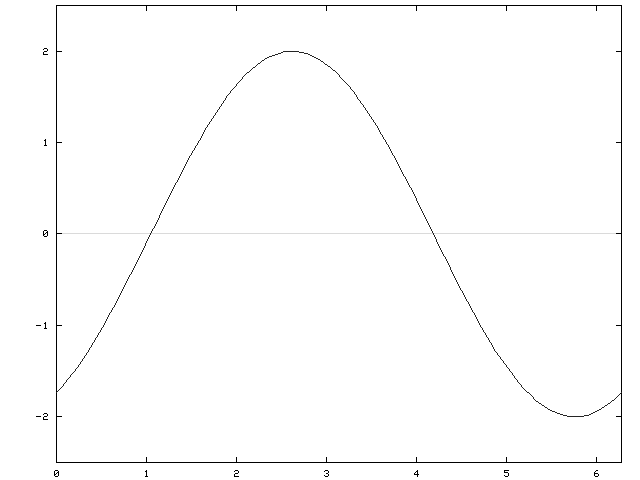
Click HERE to return to the list of problems.
SOLUTION 10 : Since
![]() the domain of f is
the domain of f is
![]() in order to insure that we not take the square root of a negative number . Now determine a sign chart for the first derivative, f' . Using the product rule, we get
in order to insure that we not take the square root of a negative number . Now determine a sign chart for the first derivative, f' . Using the product rule, we get
![]()
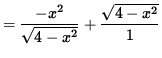
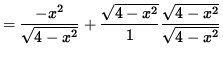
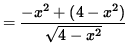
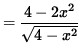
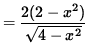
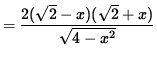
= 0
for x= 0 ,
![]() ,and
,and
![]() . In addition, note that f' is NOT DEFINED at x=2 and x=-2 since these numbers lead to division by zero. See the adjoining sign chart for the first derivative, f' .
. In addition, note that f' is NOT DEFINED at x=2 and x=-2 since these numbers lead to division by zero. See the adjoining sign chart for the first derivative, f' .
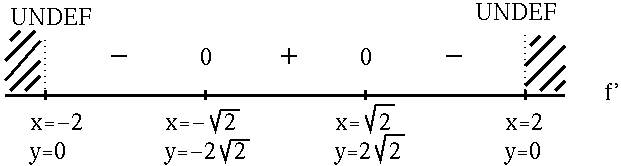
Now determine a sign chart for the second derivative, f'' . Beginning with
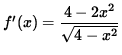
and using the quotient rule, we get
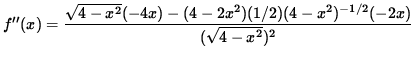
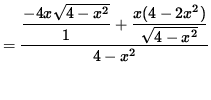
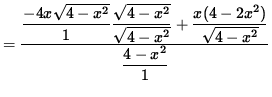
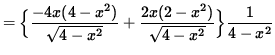
(Factor out 2x .)
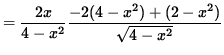
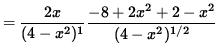
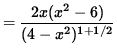
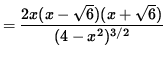
= 0 .
Then
![]() so that x= 0 ,
so that x= 0 ,
![]() , or
, or
![]() . HOWEVER,
. HOWEVER,
![]() and
and
![]() are not in the domain of function f so only x=0 solves f'(x)=0 . In addition, note that f'' is NOT DEFINED at x=2 and x=-2 . See the adjoining sign chart for the second derivative, f'' .
are not in the domain of function f so only x=0 solves f'(x)=0 . In addition, note that f'' is NOT DEFINED at x=2 and x=-2 . See the adjoining sign chart for the second derivative, f'' .
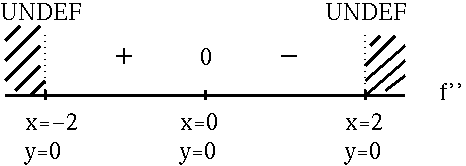
Now summarize the information from each sign chart.
FROM f' :
f is (![]() )
for
)
for
![]() ;
;
f is (
![]() )
for
)
for
![]() and
and
![]() ;
;
f has an absolute maximum at
![]() ,
,
![]() ;
;
f has a relative maximum at x=-2 , y=0 ;
f has an absolute minimum at
![]() ,
,
![]() ;
;
f has a relative minimum at x=2 , y=0 .
FROM f'' :
f is (![]() )
for -2<x<0 ;
)
for -2<x<0 ;
f is (![]() )
for 0<x<2 ;
)
for 0<x<2 ;
f has an inflection point at x=0 , y=0 .
OTHER INFORMATION ABOUT f :
If x=0 , then y=0 , so that y=0 is the y-intercept. If y=0 , then
![]() so that x=0 , x=2 , and
x=-2 are the y-intercepts. There are no horizontal or vertical asymptotes. See the adjoining detailed graph of f .
so that x=0 , x=2 , and
x=-2 are the y-intercepts. There are no horizontal or vertical asymptotes. See the adjoining detailed graph of f .
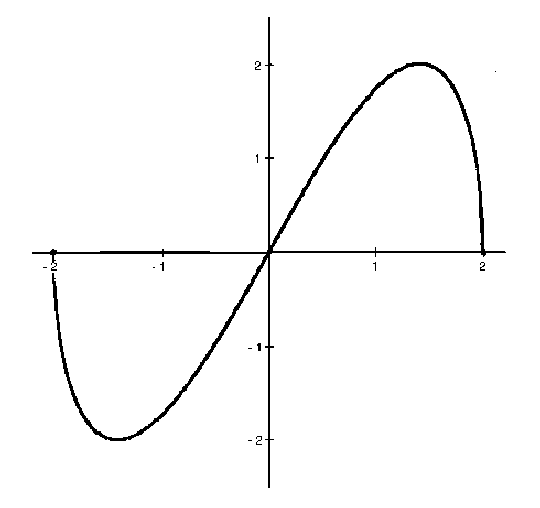
Click HERE to return to the list of problems.
SOLUTION 11 : First note that y = A x3 + 6x2 - Bx is a polynomial so that it is infinitely-differentiable. The first derivative is
y'= 3Ax2 + 12x - B ,
and the second derivative is
y''= 6Ax + 12 .
If the graph of y has a maximum value at x= -1, then y'(1)=0 so that 3A(-1)2 + 12(-1) - B = 0 or
(Equation 1)
3A - B = 12 .
If the graph of y has an inflection point at x=1, then y''(1)=0 so that 6A(1) + 12 = 0 or
A = -2 .
Substituting this value for A into Equation 1, we get 3(-2) - B = 12 or
B = -18 .
Thus, assuming that y'(-1)=0 and y''(1)=0 , the polynomial must be of the form
y = -2x3 + 6x2 + 18x
with first derivative
y' = -6x2 + 12x + 18
and second derivative
y'' = -12x + 12 .
Check to see if x=-1 determines a maximum value for y . Using the Second Derivative Test for Extrema, we have that y'(-1)=0 and y''(-1) = -12(-1) + 12 = 24 > 0 ! Thus, x=-1 determines a MINIMUM value for y , NOT a maximum value . This problem has NO SOLUTION.
Click HERE to return to the list of problems.