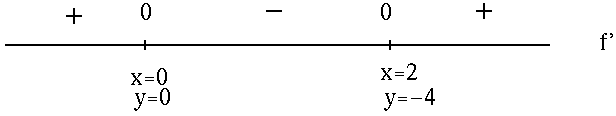
SOLUTION 1 : The domain of f is all x-values. Now determine a sign chart for the first derivative, f' :
f'(x) = 3x2 - 6x
= 3x (x - 2)
= 0
for x=0 and x=2 . See the adjoining sign chart for the first derivative, f' .
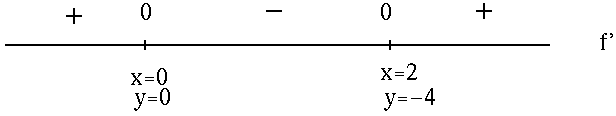
Now determine a sign chart for the second derivative, f'' :
f''(x) = 6x - 6
= 6 (x - 1)
= 0
for x=1 . See the adjoining sign chart for the second derivative, f'' .
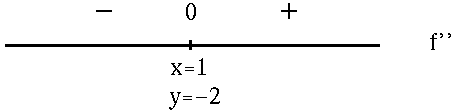
Now summarize the information from each sign chart.
FROM f' :
f is (![]() )
for x<0 and x>2 ;
)
for x<0 and x>2 ;
f is (
![]() )
for 0<x<2 ;
)
for 0<x<2 ;
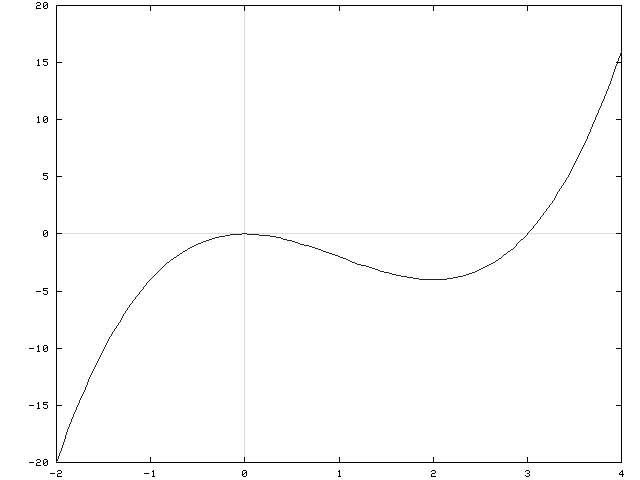
f has a relative maximum at x=0 , y=0 ;
f has a relative minimum at x=2 , y=-4 .
FROM f'' :
f is (![]() )
for x>1 ;
)
for x>1 ;
f is (![]() )
for x<1 ;
)
for x<1 ;
f has an inflection point at x=1 , y=-2 .
OTHER INFORMATION ABOUT f :
If x=0 , then y=0 so that y=0 is the y-intercept. If y=0 , then
x3-3x2=x2(x-3)=0 so that x=0 and x=3 are the x-intercepts. There are no vertical or horizontal asymptotes since f is a polynomial. See the adjoining detailed graph of f .
Click HERE to return to the list of problems.
SOLUTION 2 : The domain of f is all x-values. Now determine a sign chart for the first derivative, f' :
f'(x) = 4x3 - 12x2
= 4x2 (x - 3)
= 0
for x=0 and x=3 . See the adjoining sign chart for the first derivative, f' .
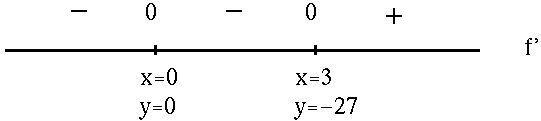
Now determine a sign chart for the second derivative, f'' :
f''(x) = 12x2 - 24x
=12x (x - 2)
= 0
for x=0 and x=2 . See the adjoining sign chart for the second derivative, f'' .
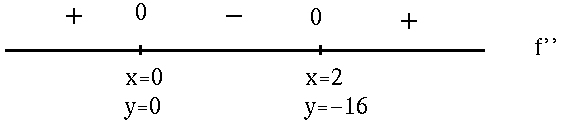
Now summarize the information from each sign chart.
FROM f' :
f is (![]() )
for x>3 ;
)
for x>3 ;
f is (
![]() )
for x<0 and 0<x<3 ;
)
for x<0 and 0<x<3 ;
f has an absolute minimum at x=3 , y=-27 .
FROM f'' :
f is (![]() )
for x<0 and x>2 ;
)
for x<0 and x>2 ;
f is (![]() )
for 0<x<2 ;
)
for 0<x<2 ;
f has inflection points at x=0 , y=0 and x=2 , y=-16 .
OTHER INFORMATION ABOUT f :
If x=0 , then y=0 so that y=0 is the y-intercept. If y=0 , then
x4-4x3=x3(x-4)=0 so that x=0 and x=4 are the x-intercepts. There are no vertical or horizontal asymptotes since f is a polynomial. See the adjoining detailed graph of f .
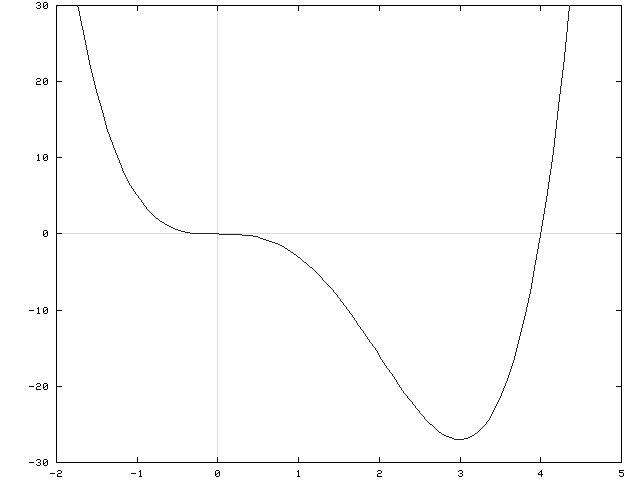
Click HERE to return to the list of problems.
SOLUTION 3 : The domain of f is all x-values. Now determine a sign chart for the first derivative, f' . Using the ordinary product rule, we get
f'(x) = x3 2 (x-2) + 3x2 (x-2)2
(Factor out x2 and (x-2) .)
= x2 (x-2) [ 2x + 3(x-2) ]
= x2 (x-2) [ 5x-6 ]
= 0
for x=0 , x= 6/5 , and x=2 . See the adjoining sign chart for the first derivative, f' .
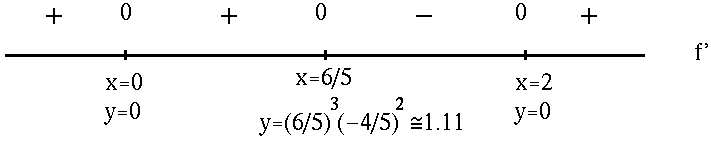
Now determine a sign chart for the second derivative, f'' . Using the triple product rule, we get
f''(x) = 2x(x-2)[5x-6] + x2(1)[5x-6] + x2(x-2)[5]
(Factor out x .)
= x [ 2(x-2)(5x-6) + x (5x-6) + 5x(x-2) ]
= x [ 2(5x2-16x+12) + 5x2-6x + 5x2-10x ]
= x [ 20x2-48x+24 ]
= 4x [ 5x2-12x+6 ]
= 0
for x=0 , and (using the quadratic formula)
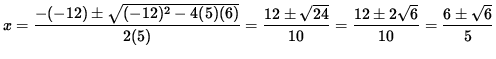 . See the adjoining sign chart for the second derivative, f'' .
. See the adjoining sign chart for the second derivative, f'' .
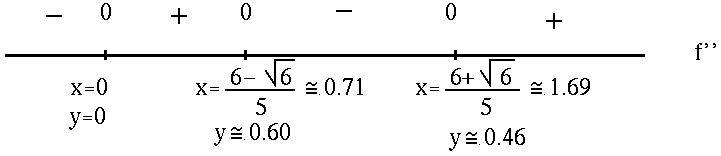
Now summarize the information from each sign chart.
FROM f' :
f is (![]() )
for x<0 , 0<x<6/5 , and x>2 ;
)
for x<0 , 0<x<6/5 , and x>2 ;
f is (
![]() )
for 6/5 <x<2 ;
)
for 6/5 <x<2 ;
f has a relative maximum at x=6/5 ,
![]() ;
;
f has a relative minimum at x=2 , y=0 .
FROM f'' :
f is (![]() )
for
)
for
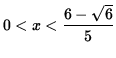 and
and
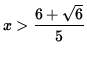 ;
;
f is (![]() )
for x<0 and
)
for x<0 and
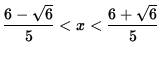 ;
;
f has inflection points at x=0 , y=0 and
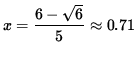 ,
,
![]() and
and
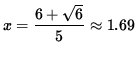 ,
,
![]() .
.
OTHER INFORMATION ABOUT f :
If x=0 , then y=0 so that y=0 is the y-intercept. If y=0 , then
x3(x-2)2=0 so that x=0 and x=2 are the x-intercepts. There are no vertical or horizontal asymptotes since f is a polynomial. See the adjoining detailed graph of f .
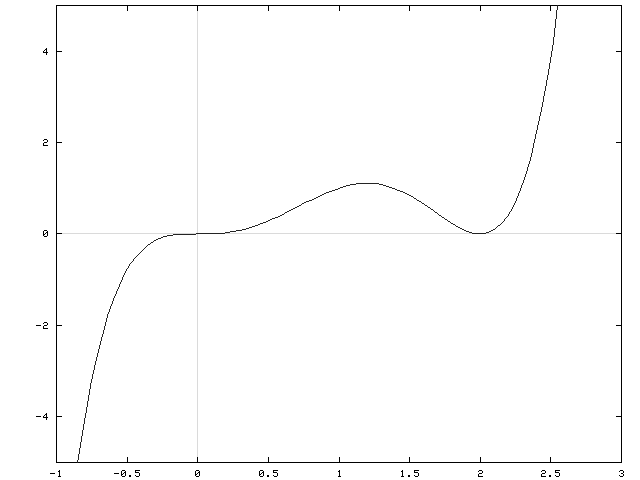
Click HERE to return to the list of problems.
SOLUTION 4 : The domain of f is all x-values. Now determine a sign chart for the first derivative, f' . Using the quotient rule, we get
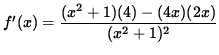
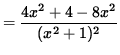
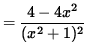
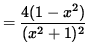
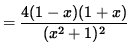
= 0
for x= 1 , and x=-1 . See the adjoining sign chart for the first derivative, f' .
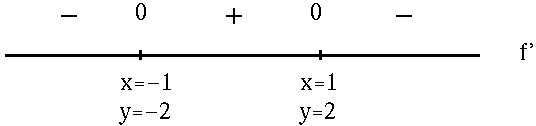
Now determine a sign chart for the second derivative, f'' . Beginning with
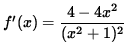
and using the quotient rule, we get
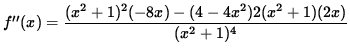
(Factor out 2x and (x2+1) .)
![$ = \displaystyle{ 2x(x^2+1) [ -4(x^2+1)- 2(4-4x^2) ] \over (x^2+1)^4 } $](img21.gif)
![$ = \displaystyle{ 2x [ -4x^2-4- 8+8x^2 ] \over (x^2+1)^3 } $](img22.gif)
![$ = \displaystyle{ 2x [ 4x^2-12 ] \over (x^2+1)^3 } $](img23.gif)
![$ = \displaystyle{ 2x (4) [ x^2-3 ] \over (x^2+1)^3 } $](img24.gif)
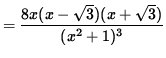
= 0
for x=0 ,
![]() , and
, and
![]() . See the adjoining sign chart for the second derivative, f'' .
. See the adjoining sign chart for the second derivative, f'' .
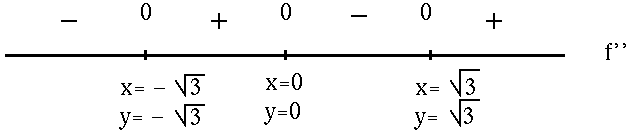
Now summarize the information from each sign chart.
FROM f' :
f is (![]() )
for -1<x<1 ;
)
for -1<x<1 ;
f is (
![]() )
for x<-1 and x>1 ;
)
for x<-1 and x>1 ;
f has an absolute maximum at x=1 , y=2 ;
f has an absolute minimum at x=-1 , y=-2 .
FROM f'' :
f is (![]() )
for
)
for
![]() and
and
![]() ;
;
f is (![]() )
for
)
for
![]() and
and
![]() ;
;
f has inflection points at x=0 , y=0 and
![]() ,
,
![]() and
and
![]() ,
,
![]() .
.
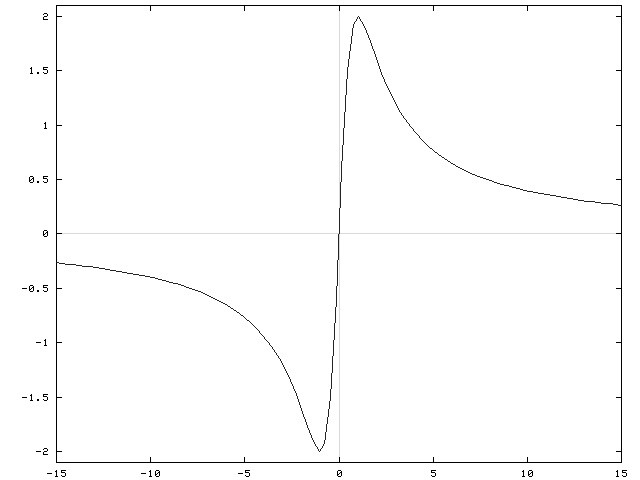
OTHER INFORMATION ABOUT f :
If x=0 , then y=0 so that y=0 is the y-intercept. If y=0 , then
![]() so that 4x=0 and x=0 is the x-intercept. There is a horizontal asymptote since
so that 4x=0 and x=0 is the x-intercept. There is a horizontal asymptote since
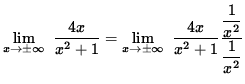
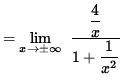
![]()
= 0 .
Thus, the line y = 0 is a a horizontal asymptote for the graph of f . See the adjoining detailed graph of f .
Click HERE to return to the list of problems.
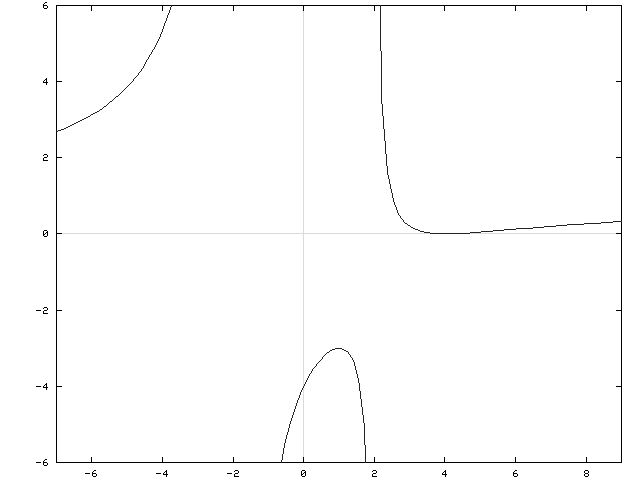
SOLUTION 5 : The domain of f is all x-values EXCEPT x=2 , because of division by zero. Now determine a sign chart for the first derivative, f' . Using the quotient rule, we get
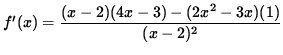
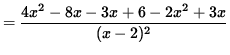
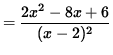
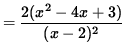
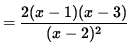
= 0
for x= 1 , and x=3 . In addition, note that f' is NOT DEFINED at x=2 . See the adjoining sign chart for the first derivative, f' .
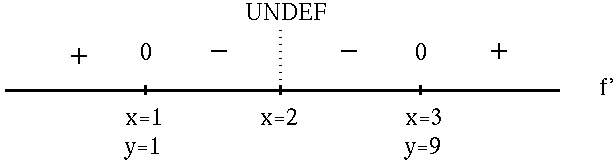
Now determine a sign chart for the second derivative, f'' . Beginning with
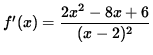
and using the quotient rule, we get
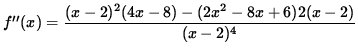
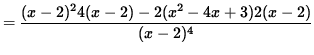
(Factor out 4 and (x-2) .)
![$ = \displaystyle{ 4(x-2) [(x-2)(x-2) - (x^2-4x+3) ] \over (x-2)^4 } $](img46.gif)
(Divide out a factor of (x-2) .)
![$ = \displaystyle{ 4 [x^2-4x+4 - x^2+4x-3) ] \over (x-2)^3 } $](img47.gif)
![$ = \displaystyle{ 4 [1 ] \over (x-2)^3 } $](img48.gif)
![]()
= 0
for NO x-values. However, note that f'' is NOT DEFINED at x=2 . See the adjoining sign chart for the second derivative, f'' .
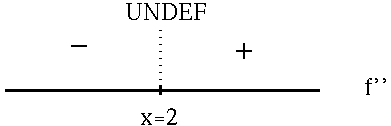
Now summarize the information from each sign chart.
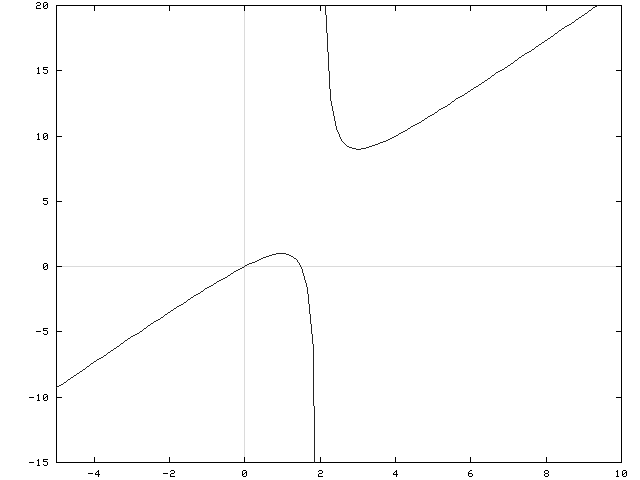
FROM f' :
f is (![]() )
for x<1 and x>3 ;
)
for x<1 and x>3 ;
f is (
![]() )
for 1<x<2 and 2<x<3 ;
)
for 1<x<2 and 2<x<3 ;
f has a relative maximum at x=1 , y=1 ;
f has a relative minimum at x=3 , y=9 .
FROM f'' :
f is (![]() )
for x>2 ;
)
for x>2 ;
f is (![]() )
for x<2 ;
)
for x<2 ;
f has no inflection points.
OTHER INFORMATION ABOUT f :
If x=0 , then y=0 so that y=0 is the y-intercept. If y=0 , then
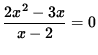 so that
2x2-3x=x(2x-3)=0 . Thus, x=0 and x=3/2 are x-intercepts. There is no horizontal asymptote since
so that
2x2-3x=x(2x-3)=0 . Thus, x=0 and x=3/2 are x-intercepts. There is no horizontal asymptote since
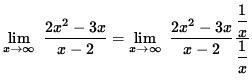
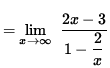
![]()
![]() ,
,
and
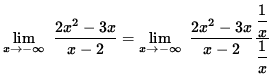
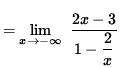
![]()
![]() .
.
Remember, a horizontal asymptote exists only if the limit to ![]() or
or ![]() is a finite number. Now check for a vertical asymptote by computing one-sided limits at the zero of the denominator, i.e., at x=2 . Thus,
is a finite number. Now check for a vertical asymptote by computing one-sided limits at the zero of the denominator, i.e., at x=2 . Thus,
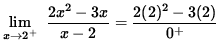
![]()
(The numerator approaches 2 and the denominator is a positive number approaching 0 .)
![]() ,
,
and
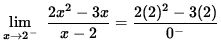
![]()
(The numerator approaches 2 and the denominator is a negative number approaching 0 .)
![]() .
.
This shows that the line x = 2 is a vertical asymptote for the graph of f . Remember, if EITHER of these one-sided limits is ![]() or
or ![]() ,
a vertical asymptote exists. See the adjoining detailed graph of f .
,
a vertical asymptote exists. See the adjoining detailed graph of f .
Click HERE to return to the list of problems.
SOLUTION 6 : The domain of f is all x-values EXCEPT x=2 and x=-2 , because of division by zero. Now determine a sign chart for the first derivative, f' . Using the quotient rule, we get
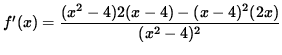
(Factor out 2 and (x-4) .)
![$ = \displaystyle{ 2(x-4) [(x^2-4) - x(x-4) ] \over (x^2-4)^2 } $](img67.gif)
![$ = \displaystyle{ 2(x-4) [ x^2-4 - x^2 + 4x ] \over (x^2-4)^2 } $](img68.gif)
![$ = \displaystyle{ 2(x-4) [ 4x-4 ] \over (x^2-4)^2 } $](img69.gif)
![$ = \displaystyle{ 2(x-4)(4) [ x-1 ] \over (x^2-4)^2 } $](img70.gif)
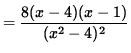
= 0
for x= 1 , and x=4 . In addition, note that f' is NOT DEFINED at x=2 and x=-2 . See the adjoining sign chart for the first derivative, f' .
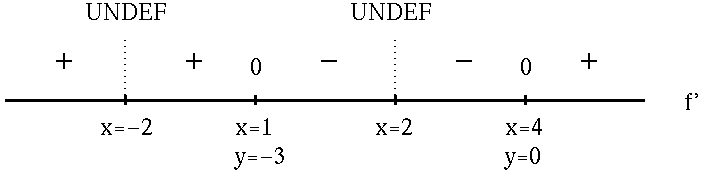
Now determine a sign chart for the second derivative, f'' . Beginning with
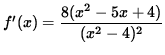
and using the quotient rule, we get
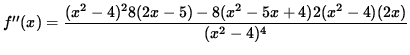
(Factor out 2 and (x2-4) .)
![$ = \displaystyle{ 2(x^2-4) [ 4(x^2-4)(2x-5) - 16x( x^2 - 5x + 4 ) ] \over (x^2-4)^4 } $](img74.gif)
(Divide out a factor of (x2-4) .)
![$ = \displaystyle{ 2 [ 4(2x^3-5x^2-8x+20) - 16x^3 +80x^2 -64x ] \over (x^2-4)^3 } $](img75.gif)
![$ = \displaystyle{ 2 [ 8x^3-20x^2-32x+80 - 16x^3 +80x^2 -64x ] \over (x^2-4)^3 } $](img76.gif)
![$ = \displaystyle{ 2 [ -8x^3 + 60x^2 -96x + 80 ] \over (x^2-4)^3 } $](img77.gif)
![$ = \displaystyle{ 2 (4) [ -2x^3 + 15x^2 -24x + 20 ] \over (x^2-4)^3 } $](img78.gif)
![$ = \displaystyle{ 8 [ -2x^3 + 15x^2 -24x + 20 ] \over (x^2-4)^3 } $](img79.gif)
= 0 ,
so that
-2x3 + 15x2 -24x + 20 = 0 . To solve this equation use Newton's method or an equation solver like that found on a TI85 graphing calculator, getting a single real solution
![]() . In addition, note that f'' is NOT DEFINED at x=2 and x=-2 . See the adjoining sign chart for the second derivative, f'' .
. In addition, note that f'' is NOT DEFINED at x=2 and x=-2 . See the adjoining sign chart for the second derivative, f'' .
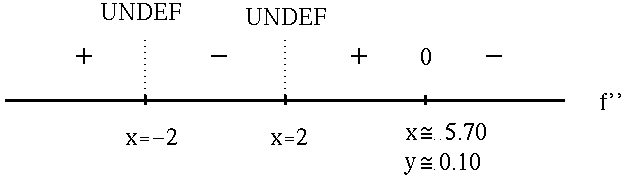
Now summarize the information from each sign chart.
FROM f' :
f is (![]() )
for x<-2 , -2<x<1 , and x>4 ;
)
for x<-2 , -2<x<1 , and x>4 ;
f is (
![]() )
for 1<x<2 and 2<x<4 ;
)
for 1<x<2 and 2<x<4 ;
f has a relative maximum at x=1 , y=-3 ;
f has a relative minimum at x=4 , y=0 .
FROM f'' :
f is (![]() )
for x<-2 and 2<x<5.70 ;
)
for x<-2 and 2<x<5.70 ;
f is (![]() )
for -2<x<2 and x>5.70 ;
)
for -2<x<2 and x>5.70 ;
f has an inflection point at
![]() ,
,
![]() .
.
OTHER INFORMATION ABOUT f :
If x=0 , then y=-4 so that y=-4 is the y-intercept. If y=0 , then
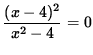 so that (x-4)2=0 . Thus, x=4 is the x-intercept. There is a horizontal asymptote since
so that (x-4)2=0 . Thus, x=4 is the x-intercept. There is a horizontal asymptote since
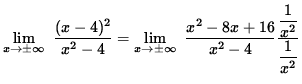
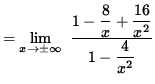
![]()
= 1 .
Thus, the line y=1 is a horizontal asymptote for the graph of f . Now check for vertical asymptotes by computing one-sided limits at the zeroes of the denominator, i.e., at x=2 and at x=-2 . Thus,
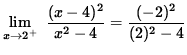
![]()
(The numerator approaches 4 and the denominator is a positive number approaching 0 .)
![]() ,
,
and
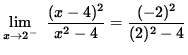
![]()
(The numerator approaches 4 and the denominator is a negative number approaching 0 .)
![]() .
.
This shows that the line x = 2 is a vertical asymptote for the graph of f . Remember, if EITHER of these one-sided limits is ![]() or
or ![]() ,
a vertical asymptote exists. Now check at x=-2 . Thus,
,
a vertical asymptote exists. Now check at x=-2 . Thus,
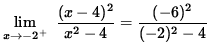
![]()
(The numerator approaches 36 and the denominator is a negative number approaching 0 .)
![]() ,
,
and
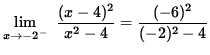
![]()
(The numerator approaches 36 and the denominator is a positive number approaching 0 .)
![]() .
.
This shows that the line x = -2 is a vertical asymptote for the graph of f . See the adjoining detailed graph of f .
Click HERE to return to the list of problems.