SOLUTION 4: We are given the equation $ e^x+x+2=0 $. Let function
$$ f(x)=e^x+x+2 \ \ \ \ and \ choose \ \ \ \ m=0 $$
This function is continuous for all values of $x$ since it is the SUM of a polynomial ($x+2$) and a well-known transcendental function ($e^x$).
To establish an appropriate interval consider the graph of this function. (Please note that the graph of the function is not necessary for a valid proof, but the graph will help us understand how to use the Intermediate Value Theorem. On many subsequent problems, we will solve the problem without using the "luxury" of a graph.)
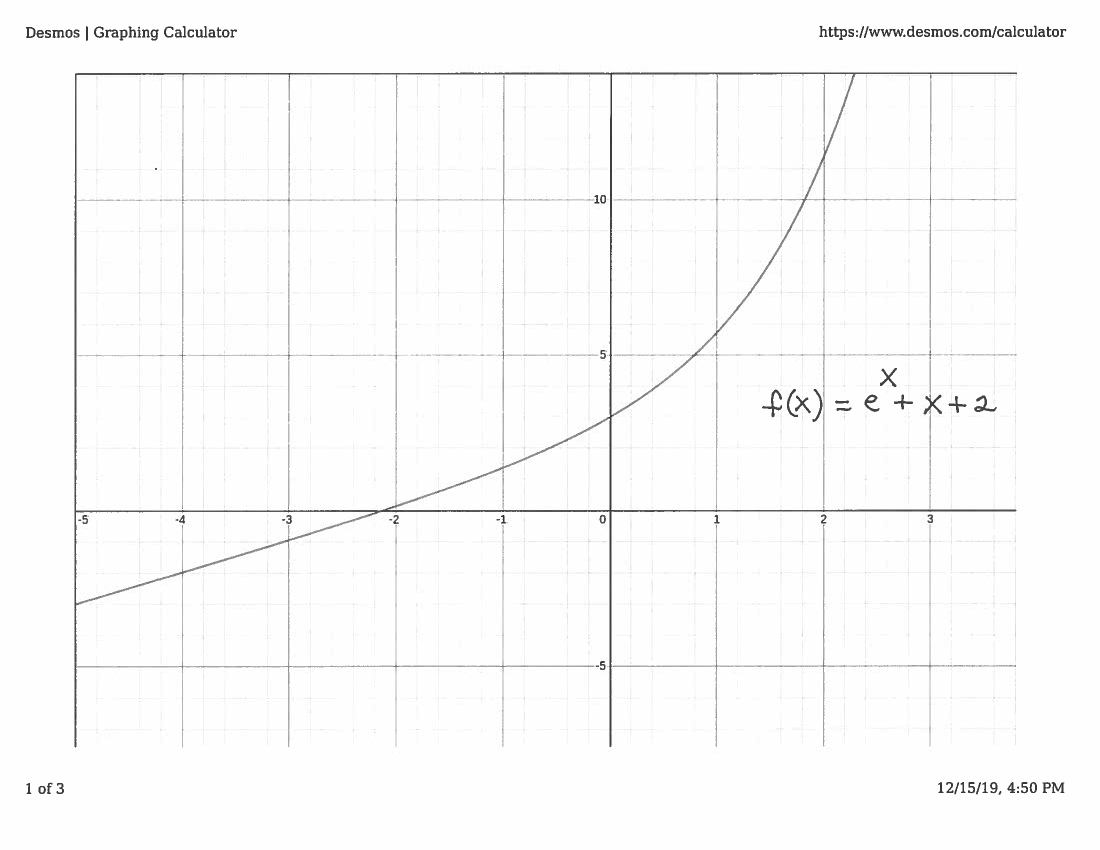
Note that $$ f(-3)= e^{-3}+(-3)+2 \approx -0.95<0 \ \ \ \ and \ \ \ \ f(0)= e^{0}+(0)+2=1+2=3>0 $$
so that $$ f(-3) \approx -0.95 < m <3=f(0) $$
i.e., $m=0$ is between $ f(-3) $ and $ f(0) $. Now choose the interval to be $ \ [-3, 0] $.
The assumptions of the Intermediate Value Theorem have now been met, so we can conclude that there is some number $c$ in the interval $[-3, 0]$ which satisfies
$$ f(c)=m $$
i.e.,
$$ e^{c}+c+2=0 $$
and the equation is solvable.
Click HERE to return to the list of problems.

