Solving Intermediate Value Theorem Problems
The Intermediate Value Theorem is one of the most important theorems in Introductory Calculus, and it forms the basis for proofs of many results in subsequent and advanced Mathematics courses. The
history of this theorem begins in the 1500's and is eventually based on the academic work of Mathematicians Bernard Bolzano, Augustin-Louis Cauchy, Joseph-Louis Lagrange, and Simon Stevin. Generally speaking, the Intermediate Value Theorem applies to continuous functions and is used to prove that equations, both algebraic and transcendental , are solvable. Note that this theorem will be used to prove the EXISTENCE of solutions, but will not actually solve the equations. (Newton's Method could be used to determine a good ESTIMATE for these solutions.)
The formal statement of this theorem together with an illustration of the theorem follow. All functions are assumed to be real-valued.
INTERMEDIATE VALUE THEOREM: Let $f$ be a continuous function on the closed interval $ [a, b] $. Assume that $m$ is a number ($y$-value) between $f(a)$ and $f(b)$. Then there is at least one number $c$ ($x$-value) in the interval $[a, b]$ which satifies
$$ f(c)=m $$
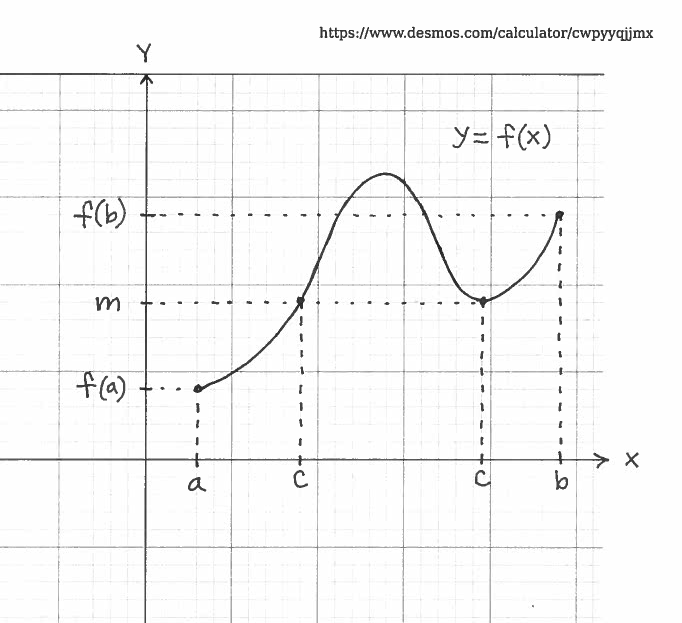
While the result certainly seems intuitively obvious, the formal proof of the Intermediate Value Theorem is quite sophisticated and is beyond the experience of most first-year calculus students.
For a simple illustration of the this theorem, assume that a function $f$ is a continuous and $m=0$. Then the conditions $ f(a)<0 $ and $ f(b)>0 $ would lead to the conclusion that the equation $f(x)=0$ is solvable for $x$, i.e., $f(c)=0$. This result is formally accredited to Berard Bolzano and is called
Bolzano's Theorem . It should be noted that Intermediate Value Theorem guarantees the existence of a solution, but not what the solution is.
Here is a summary of how I will use the Intermediate Value Theorem in the problems that follow.
$ \ \ \ \ $ 1. Define a function $ y=f(x)$.
$ \ \ \ \ $ 2. Define a number ($y$-value) $m$.
$ \ \ \ \ $ 3. Establish that $f$ is continuous.
$ \ \ \ \ $ 4. Choose an interval $ [a, b] $.
$ \ \ \ \ $ 5. Establish that $m$ is between $ f(a) $ and $ f(b) $.
$ \ \ \ \ $ 6. Now invoke the conclusion of the Intermediate Value Theorem.
In the list of Differentials Problems which follows, most problems are average and a few are somewhat challenging.
- PROBLEM 1 : Use the Intermediate Value Theorem to prove that the equation $ 3x^5-4x^2=3 $ is solvable on the interval [0, 2].
Click HERE to see a detailed solution to problem 1.
- PROBLEM 2 : Use the Intermediate Value Theorem to prove that the equation $ e^x = 4-x^3 $ is solvable on the interval [-2, -1].
Click HERE to see a detailed solution to problem 2.
- PROBLEM 3 : Use the Intermediate Value Theorem to prove that the equation $ x^3+2x-5=0 $ is solvable.
Click HERE to see a detailed solution to problem 3.
- PROBLEM 4 : Use the Intermediate Value Theorem to prove that the equation $ e^x+x+2=0 $ is solvable.
Click HERE to see a detailed solution to problem 4.
- PROBLEM 5 : Use the Intermediate Value Theorem to prove that the equation $ x^5-3x=4-x^2 $ is solvable.
Click HERE to see a detailed solution to problem 5.
- PROBLEM 6 : Use the Intermediate Value Theorem to prove that the equation $ x^3=20+ \sqrt{x} $ is solvable.
Click HERE to see a detailed solution to problem 6.
- PROBLEM 7 : Use the Intermediate Value Theorem to prove that the equation $ x^3+2= \sin{x} $ is solvable.
Click HERE to see a detailed solution to problem 7.
- PROBLEM 8 : Use the Intermediate Value Theorem to prove that the equation $ x^2-4x^3+1 = x-7 $ is solvable.
Click HERE to see a detailed solution to problem 8.
- PROBLEM 9 : Use the Intermediate Value Theorem to prove that the equation $ x e^x = x^2-1 $ is solvable.
Click HERE to see a detailed solution to problem 9.
- PROBLEM 10 : Use the Intermediate Value Theorem to prove that the equation $ x^3 \cos x = 4 $ is solvable.
Click HERE to see a detailed solution to problem 10.
- PROBLEM 11 : Use the Intermediate Value Theorem to prove that the equation $ \displaystyle{ x^4 \over x+1 } = x^2+5 $ is solvable.
Click HERE to see a detailed solution to problem 11.
- PROBLEM 12 : Use the Intermediate Value Theorem to prove that the equation $ \displaystyle{ x-1 \over x^2+2 } = \displaystyle{ 3-x \over x+1 } $ is solvable.
Click HERE to see a detailed solution to problem 12.
- PROBLEM 13 : Use the Intermediate Value Theorem to prove that the equation $ \tan x = 1-x $ is solvable.
Click HERE to see a detailed solution to problem 13.
- PROBLEM 14 : Use the Intermediate Value Theorem to prove that the equation $ x^3 = 2x^2+3x-3 $ has three solutions.
Click HERE to see a detailed solution to problem 14.
- PROBLEM 15 : Use the Intermediate Value Theorem to prove the following statement: If $ f$ is a continuous function on the interval $[0, 1]$ with
$ f(0)>0 $ and $ f(1)<1 $, then there is some number $c$ in the interval $ [0, 1] $ which satisfies $ f(c)=c $. (In mathematics this number $c$ is called a
fixed point for $f$.)
Click HERE to see a detailed solution to problem 15.
- PROBLEM 16 : Use the Intermediate Value Theorem to prove the following statement: If $ f$ is a continuous function on the interval $[0, 2]$ with
$ f(0)>0 $ and $ f(2)<4 $, then there is some number $c$ in the interval $ [0, 2] $ which satisfies $ f(c)=c^2 $.
Click HERE to see a detailed solution to problem 16.
Click HERE to return to the original list of various types of calculus problems.
Your comments and suggestions are welcome. Please e-mail any correspondence to Duane Kouba by
clicking on the following address :
kouba@math.ucdavis.edu
A heartfelt "Thank you" goes to The MathJax Consortium for making the construction of this webpage fun and easy.
Duane Kouba ...
October 24, 2019

