SOLUTION 13: We are given the equation
$$ \tan{x} = 1-x \ \ \ \ \longrightarrow \ \ \ \ \tan{x}+x-1=0 $$
Let function
$$ f(x)=\tan{x}+x-1 \ \ \ \ and \ choose \ \ \ \ m=0 $$
The function $x-1$ is continuous for all values of $x$ since it is a polynomial. Consider the fact that $\tan{x}$ is a well-known periodic function, which is piecewise continuous. Let's look at the graph of both functions to establish an appropriate interval.
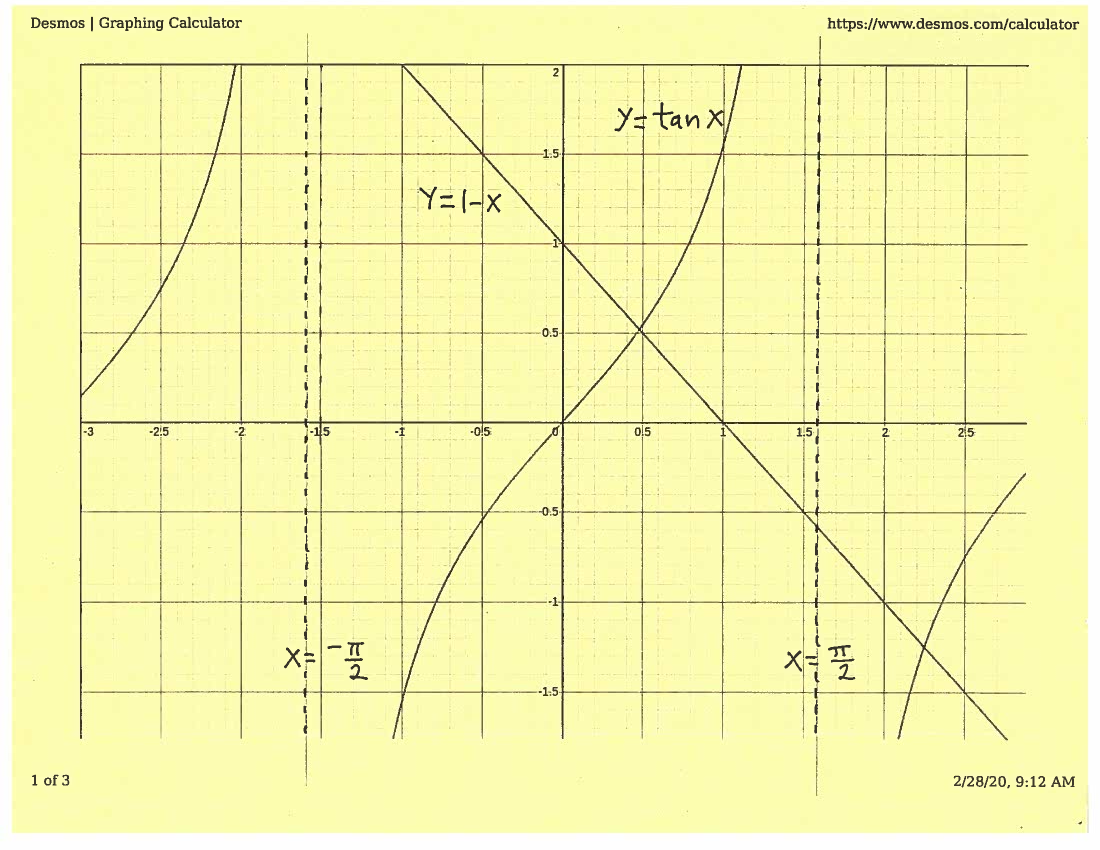
From this graph we can see that the solution lies in the interval $[0, \pi/4]$ and that $f$ is continuous on $[0, \pi/4]$ since it is the SUM of continuous functions.
Note that $$ f(0)= \tan{0}+(0)-1= \{0\}-1 =-1 \ \ \ \ and \ \ \ \ f(\pi/4)= \tan{\pi/4}+(\pi/4)-1=1+(\pi/4)-1= \pi/4>0 $$
so that $$ f(0) = -1 < m < \pi/4=f(\pi/4) $$
i.e., $m=0$ is between $ f(0) $ and $ f(\pi/4) $. Now choose the interval to be $ \ [0, \pi/4] $.
The assumptions of the Intermediate Value Theorem have now been met, so we can conclude that there is some number $c$ in the interval $[0, \pi/4]$ which satisfies
$$ f(c)=m $$
i.e.,
$$ \tan{c}+c-1=0 $$
and the equation is solvable.
Click HERE to return to the list of problems.

