-
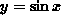 for
for 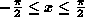
-
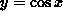 for
for 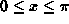
-
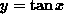 for
for 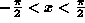
-
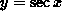 for
for 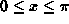 , except
, except 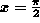
-
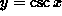 for
for 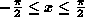 , except x = 0
, except x = 0
-
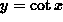 for
for 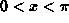
Click HERE to see a detailed solution to problem 1.
Click HERE to see a detailed solution to problem 2.
Click HERE to see a detailed solution to problem 3.
Click HERE to see a detailed solution to problem 4.
Click HERE to see a detailed solution to problem 5.
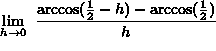 .
.
Click HERE to see a detailed solution to problem 6.
Some of the following problems require use of the chain rule.
Click HERE to see a detailed solution to problem 7.
Click HERE to see a detailed solution to problem 8.
Click HERE to see a detailed solution to problem 9.
Click HERE to see a detailed solution to problem 10.
Click HERE to see a detailed solution to problem 11.
Click HERE to see a detailed solution to problem 12.
Click HERE to see a detailed solution to problem 13.
Click HERE to see a detailed solution to problem 14.
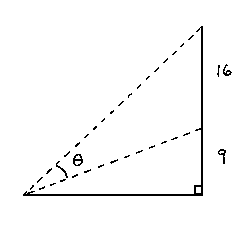
Click HERE to see a detailed solution to problem 15.
Your comments and suggestions are welcome. Please e-mail any correspondence to Duane Kouba by clicking on the following address :