![]()
![]()
![]()
= 0 .
If y' = 0 for all admissable values of x , then y must be a constant function, i.e.,
![]() for all admissable values of x ,
for all admissable values of x ,
i.e.,
arc![]() for all admissable values of x .
for all admissable values of x .
In particular, if x = 1 , then
arc![]()
i.e.,
![]() .
.
Thus, c = 0 and arc![]() for all admissable values of x . We conclude that
for all admissable values of x . We conclude that
arc![]() .
.
Note that this final conclusion follows even more simply and directly from the definitions of these two inverse trigonometric functions.
Click HERE to return to the list of problems.
SOLUTION 12 : Differentiate ![]() . Begin by applying the product rule to the first summand and the chain rule to the second summand. Then
. Begin by applying the product rule to the first summand and the chain rule to the second summand. Then
![]()
![]()
![]()
![]() .
.
Click HERE to return to the list of problems.
SOLUTION 13 : Find an equation of the line tangent to the graph of
![]() at x=2 . If x = 2 , then
at x=2 . If x = 2 , then ![]() , so that the line passes through the point
, so that the line passes through the point ![]() . The slope of the tangent line follows from the derivative
. The slope of the tangent line follows from the derivative
![]()
![]()
![]()
![]()
![]()
![]()
(Recall that when dividing by a fraction, one must invert and multiply by the reciprocal. That is ![]() .)
.)
![]()
![]() .
.
The slope of the line tangent to the graph at x = 2 is
![]() .
.
Thus, an equation of the tangent line is
![]()
or
![]()
or
![]() .
.
Click HERE to return to the list of problems.
SOLUTION 14 : Evaluate ![]() . Since
. Since ![]() and
and ![]() , it follows that
, it follows that
![]() takes the indeterminate form `` zero over zero.'' Thus, we can apply
L'H
takes the indeterminate form `` zero over zero.'' Thus, we can apply
L'H![]() pital's Rule. Begin by differentiating the numerator and denominator separately. DO NOT apply the quotient rule ! Then
pital's Rule. Begin by differentiating the numerator and denominator separately. DO NOT apply the quotient rule ! Then
![]() =
= 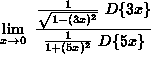
= 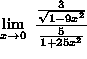
(Recall that when dividing by a fraction, one must invert and multiply by the reciprocal. That is 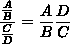 .)
.)
= 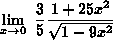
= ![]()
= ![]() .
.
Click HERE to return to the list of problems.
SOLUTION 15 : A movie screen on the front wall in your classroom is 16 feet high and positioned 9 feet above your eye-level. How far away from the front of the room should you sit in order to have the ``best" view ? Begin by introducing variables x and ![]() . (See the diagram below.)
. (See the diagram below.)
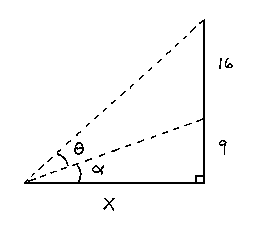
From trigonometry it follows that
![]() ,
,
so that
![]() .
.
In addition,
![]()
so that
![]() .
.
It follows that
![]()
![]() ,
,
that is, angle ![]() is explicitly represented as a function of distance x . Now find the value of x which maximizes the value of function
is explicitly represented as a function of distance x . Now find the value of x which maximizes the value of function ![]() . Begin by differentiating function
. Begin by differentiating function ![]() and setting the derivative equal to zero. Then
and setting the derivative equal to zero. Then
![]()
![]()
![]() .
.
![]() .
.
Now solve this equation for x . Then
![]()
iff
![]()
iff
![]()
iff
![]()
iff
![]()
iff
![]() feet .
feet .
(Use the first or second derivative test (The first derivative test is easier.) to verify that this value of x
determines a maximum value for ![]() .)
.)
Thus, the ``best'' view is found x=15 feet from the front of the room.
Click HERE to return to the list of problems.