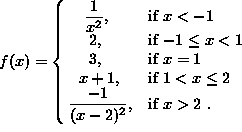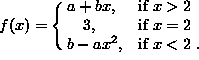LIMITS OF FUNCTIONS AS X APPROACHES A CONSTANT

The following problems require the use of the algebraic computation of limits of functions as x approaches a constant. Most problems are average. A few are somewhat challenging. All of the solutions are given WITHOUT the use of L'Hopital's Rule. If you are going to try these problems before looking at the solutions, you can avoid common mistakes by giving careful consideration to the form during the computations of these limits. Initially, many students INCORRECTLY conclude that is equal to 1 or 0 , or that the limit does not exist or is or . In fact, the form is an example of an indeterminate form. This simply means that you have not yet determined an answer. Usually, this indeterminate form can be circumvented by using algebraic manipulation. Such tools as algebraic simplification, factoring, and conjugates can easily be used to circumvent the form so that the limit can be calculated.

• PROBLEM 1 : Compute .

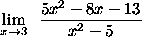  Click HERE to see a detailed solution to problem 1.
  
  
  

• PROBLEM 2 : Compute .

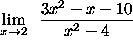  Click HERE to see a detailed solution to problem 2.
  
  
  

• PROBLEM 3 : Compute .

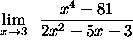  Click HERE to see a detailed solution to problem 3.
  
  
  

• PROBLEM 4 : Compute .

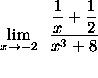  Click HERE to see a detailed solution to problem 4.
  
  
  

• PROBLEM 5 : Compute .

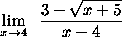  Click HERE to see a detailed solution to problem 5.
  
  
  

• PROBLEM 6 : Compute .

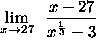  Click HERE to see a detailed solution to problem 6.
  
  
  

• PROBLEM 7 : Compute .

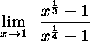  Click HERE to see a detailed solution to problem 7.
  
  
  

• PROBLEM 8 : Compute .

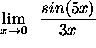  Click HERE to see a detailed solution to problem 8.
  
  
  

• PROBLEM 9 : Compute .

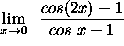  Click HERE to see a detailed solution to problem 9.
  
  
  

• PROBLEM 10 : Compute .

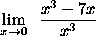  Click HERE to see a detailed solution to problem 10.
  
  
  

• PROBLEM 11 : Compute .

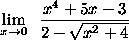  Click HERE to see a detailed solution to problem 11.
  
  
  

• PROBLEM 12 : Compute .

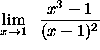  Click HERE to see a detailed solution to problem 12.
  
  
  

• PROBLEM 13 : Compute .

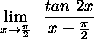  This problem requires an unusual replacement, trigonometry identities, and trigonometry limits.
  

  Click HERE to see a detailed solution to problem 13.

The next problem requires an understanding of one-sided limits.

• PROBLEM 14 : Consider the function

  i.) Sketch the graph of f .

  ii.) Determine the following limits.

  • a.)

  • b.)

  • c.)

  • d.)

  • e.)

  • f.)

  • g.)

  • h.)

  • i.)

  • j.)

  • k.)

  • l.)

  Click HERE to see a detailed solution to problem 14.
  
  
  

• PROBLEM 15 : Consider the function

  Determine the values of constants a and b so that exists and is equal to f(2).

  Click HERE to see a detailed solution to problem 15.

Click HERE to return to the original list of various types of calculus problems.

Your comments and suggestions are welcome. Please e-mail any correspondence to Duane Kouba by clicking on the following address :

kouba@math.ucdavis.edu

• About this document ...