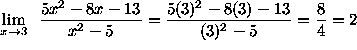 .
.
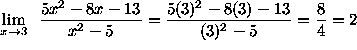 .
.
Click HERE to return to the list of problems.
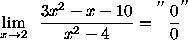
(Circumvent the indeterminate form by factoring both the numerator and denominator.)
![]()
(Divide out the factors x - 2 , the factors which are causing the indeterminate form ![]() . Now the limit can be
computed. )
. Now the limit can be
computed. )
![]()
![]()
![]()
Click HERE to return to the list of problems.
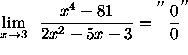
(Circumvent the indeterminate form by factoring both the numerator and denominator.)
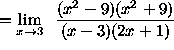
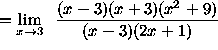
(Divide out the factors x - 3 , the factors which are causing the indeterminate form ![]() . Now the limit can be
computed. )
. Now the limit can be
computed. )
![]()
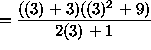
![]() .
.
Click HERE to return to the list of problems.
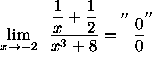
(Algebraically simplify the fractions in the numerator using a common denominator.)
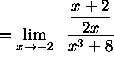
(Division by ![]() is the same as multiplication by
is the same as multiplication by ![]() .)
.)
![]()
(Factor the denominator . Recall that
![]() .)
.)
![]()
(Divide out the factors x + 2 , the factors which are causing the indeterminate form ![]() . Now the limit can be
computed. )
. Now the limit can be
computed. )
![]()
![]()
![]() .
.
Click HERE to return to the list of problems.
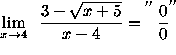
(Eliminate the square root term by multiplying by the conjugate of the numerator over itself. Recall that
![]() . )
. )
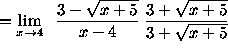
![]()
![]()
![]()
(Divide out the factors x - 4 , the factors which are causing the indeterminate form ![]() . Now the limit can be
computed. )
. Now the limit can be
computed. )
![]()
![]()
![]() .
.
Click HERE to return to the list of problems.
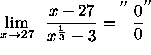
(It may appear that multiplying by the conjugate of the numerator over itself is a reasonable next step.
It's a good idea, but doesn't work. Instead, write x - 27 as the difference of cubes and recall that
![]() .)
.)
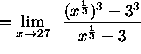
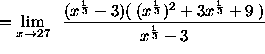
(Divide out the factors ![]() , the factors which are causing the indeterminate form
, the factors which are causing the indeterminate form ![]() . Now the limit can be computed. )
. Now the limit can be computed. )
![]()
![]()
= 27 .
Click HERE to return to the list of problems.
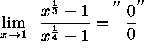
(Multiplying by conjugates won't work for this challenging problem. Instead, recall that
![]() and
and ![]() , and note that
, and note that
![]() and
and ![]() . This should help explain the next
few mysterious steps.)
. This should help explain the next
few mysterious steps.)
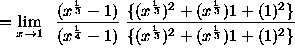
![]()
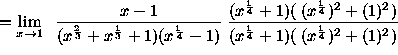
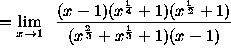
(Divide out the factors x - 1 , the factors which are causing the indeterminate form ![]() . Now the limit can be
computed. )
. Now the limit can be
computed. )
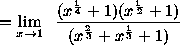
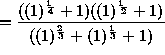
![]() .
.
Click HERE to return to the list of problems.
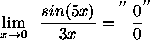
(If you wrote that ![]() , you are incorrect. Instead, multiply and divide by 5.)
, you are incorrect. Instead, multiply and divide by 5.)
![]()
![]()
(Use the well-known fact that ![]() .)
.)
![]()
![]() .
.
Click HERE to return to the list of problems.
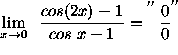
(Recall the trigonometry identity ![]() .)
.)
![]()
![]()
![]()
(The numerator is the difference of squares. Factor it.)
![]()
(Divide out the factors ![]() , the factors which are causing the indeterminate form
, the factors which are causing the indeterminate form ![]() .
Now the limit can be computed. )
.
Now the limit can be computed. )
![]()
![]()
![]() .
.
Click HERE to return to the list of problems.
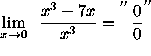
(Factor x from the numerator and denominator, then divide these factors out.)
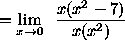
![]()
(The numerator approaches -7 and the denominator is a positve quantity approaching 0 .)
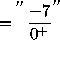
(This is NOT an indeterminate form. The answer follows.)
![]() .
.
(Thus, the limit does not exist.)
Click HERE to return to the list of problems.
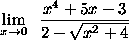
(The numerator approaches -3 and the denominator is a negative quantity which approaches 0 as x
approaches 0 .)
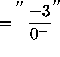
(This is NOT an indeterminate form. The answer follows.)
![]() .
.
(Thus, the limit does not exist.)
Click HERE to return to the list of problems.
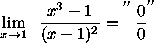
(Recall that ![]() . )
. )
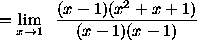
(Divide out the factors x - 1 , the factors which are causing the indeterminate form ![]() . Now the limit
can be computed. )
. Now the limit
can be computed. )
![]() .
.
(The numerator approaches 3 and the denominator approaches 0 as x approaches 1 . However, the quantity
in the denominator is sometimes negative and sometimes positive. Thus, the correct answer is NEITHER
![]() NOR
NOR ![]() . The correct answer follows.)
. The correct answer follows.)
The limit does not exist.
Click HERE to return to the list of problems.
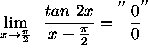
(Make the replacement ![]() so that
so that ![]() . Note that as
x approaches
. Note that as
x approaches ![]() , h approaches 0 . )
, h approaches 0 . )
![]()
(Recall the well-known, but seldom-used, trigonometry identity
![]() .)
.)
![]()
![]()
![]()
![]()
(Recall the well-known trigonometry identity ![]() . )
. )
![]()
![]()
(Recall that ![]() . )
. )
![]()
![]()
= 2 .
Click HERE to return to the list of problems.
SOLUTION 14 : Consider the function 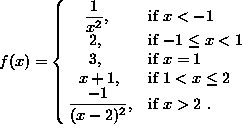
i.) The graph of f is given below.
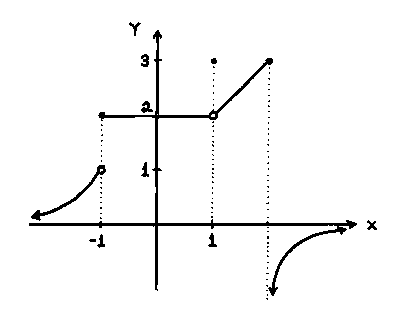
ii.) Determine the following limits.
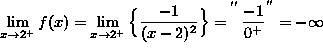 (The numerator is always -1 and the denominator is always a positive number approaching 0.) , so the limit does not exist.
(The numerator is always -1 and the denominator is always a positive number approaching 0.) , so the limit does not exist.
Click HERE to return to the list of problems.
SOLUTION 15 : Consider the function 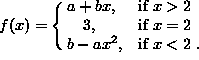
Determine the values of constants a and b so that
![]() exists. Begin by computing one-sided limits at x=2 and setting each equal to 3. Thus,
exists. Begin by computing one-sided limits at x=2 and setting each equal to 3. Thus,
![]()
and
![]() .
.
Now solve the system of equations
a+2b = 3 and b-4a = 3 .
Thus,
a = 3-2b so that b-4(3-2b) = 3
iff b-12+ 8b = 3
iff 9b = 15
iff ![]() .
.
Then
![]() .
.
Click HERE to return to the list of problems.