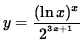 .
.
SOLUTION 8 : Because a variable is raised to a variable power in this function, the ordinary rules of differentiation DO NOT APPLY ! The function must first be revised before a derivative can be taken. Begin with
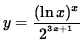 .
.
Apply the natural logarithm to both sides of this equation and use the algebraic properties of logarithms, getting
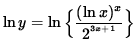
![]()
![]() .
.
Differentiate both sides of this equation. The left-hand side requires the chain rule since y represents a function of x . Use the product rule and the chain rule on the right-hand side. Thus, beginning with
![]()
and differentiating, we get
![]()
![]()
(Get a common denominator and combine fractions on the right-hand side.)
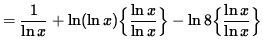
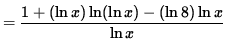 .
.
Multiply both sides of this equation by y, getting
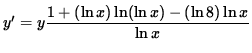
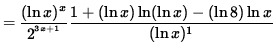
(Combine the powers of ![]() .)
.)
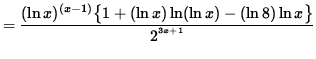 .
.
Click HERE to return to the list of problems.
SOLUTION 9 : Because a variable is raised to a variable power in this function, the ordinary rules of differentiation DO NOT APPLY ! The function must first be revised before a derivative can be taken. Begin with
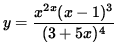 .
.
Apply the natural logarithm to both sides of this equation and use the algebraic properties of logarithms, getting
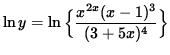
![]()
![]()
![]() .
.
Differentiate both sides of this equation. The left-hand side requires the chain rule since y represents a function of x . Use the product rule and the chain rule on the right-hand side. Thus, beginning with
![]()
and differentiating, we get
![]()
![]()
(Get a common denominator and combine fractions on the right-hand side.)
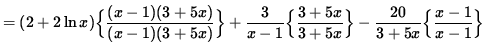
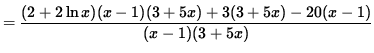
(Simplify the polynomials in the numerator.)
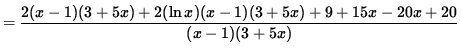
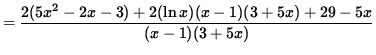
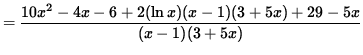
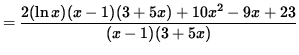 .
.
Multiply both sides of this equation by y, getting
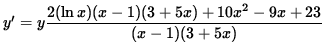
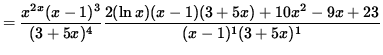
(Combine the powers of (x-1)bvand (3+ 5x) .)
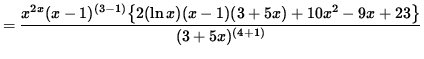
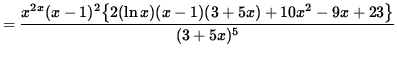 .
.
Click HERE to return to the list of problems.
SOLUTION 10 : First note that
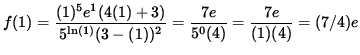 ,
,
so that the tangent line passes through the point
x=1 and y = (7/4)e .
Nowhere in the function f is a variable raised to a variable power. Thus, the ordinary rules of differentiation DO APPLY ! However, the function is so algebraically complicated that use of the ordinary rules of differentiation would be somewhat unpleasant. Even though it is not necessary, differentiation will be considerably easier if we FIRST APPLY THE NATURAL LOGARITHM. Begin with
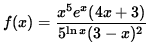 .
.
Apply the natural logarithm to both sides of this equation and use the algebraic properties of logarithms, getting
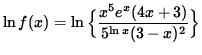
![]()
(Note that
![]() .)
.)
![]()
![]()
![]()
![]() .
.
Differentiate both sides of this equation. The left-hand side requires the chain rule since f(x) represents a function of x . Use the chain rule on the right-hand side. Thus, beginning with
![]()
and differentiating, we get
![]()
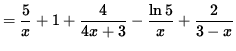 .
.
Multiply both sides of this equation by f(x), getting
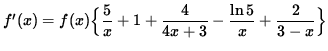 .
.
The SLOPE of the line tangent to the graph of f at x=1 is
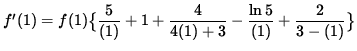
![]()
![]() .
.
Thus, the EQUATION of the line tangent to the graph of f at x=1 is
![]() .
.
Click HERE to return to the list of problems.
SOLUTION 11 : In this function the only term that requires logarithmic differentiation is x1/x . Begin with
y = x1/x .
Apply the natural logarithm to both sides of this equation and use the algebraic properties of logarithms, getting
![]()
![]()
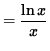 .
.
Differentiate both sides of this equation. The left-hand side requires the chain rule since y represents a function of x . Use the quotient rule on the right-hand side. Thus, beginning with
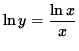
and differentiating, we get
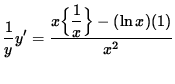
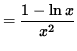 .
.
Multiply both sides of this equation by y, getting
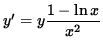

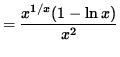 .
.
Now return to the original function
![]() . Differentiating, we get
. Differentiating, we get
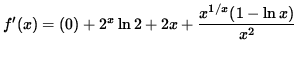
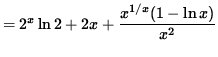 .
.
The slope of the line TANGENT to the graph of f at x=1 is
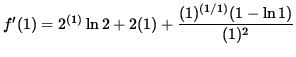
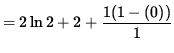
![]()
![]() .
.
Thus, the slope of the line PERPENDICULAR to the graph of f at x=1 is
![]() .
.
Click HERE to return to the list of problems.
SOLUTION 12 : Because a variable is raised to a variable power in this function, the ordinary rules of differentiation DO NOT APPLY ! The function must first be revised before a derivative can be taken. Begin with
![]() .
.
Apply the natural logarithm to both sides of this equation and use the algebraic properties of logarithms, getting
![]()
![]() .
.
We CANNOT yet differentiate this expression since a variable is still raised to a variable power. Apply the natural logarithm AGAIN to both sides of this equation ! Begin with
![]() .
.
Apply the natural logarithm to both sides of this equation and use the algebraic properties of logarithms, getting
![]()
![]()
![]() .
.
Differentiate both sides of this equation. The left-hand side requires the chain rule since y represents a function of x . Use the product rule and the chain rule on the right-hand side. Thus, beginning with
![]()
and differentiating, we get
![]()
![]()
(Get a common denominator and combine fractions on the right-hand side.)
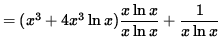
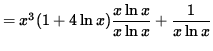
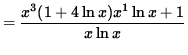
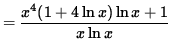 .
.
Multiply both sides of this equation by ![]() ,
getting
,
getting
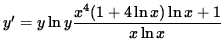
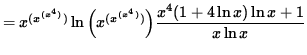
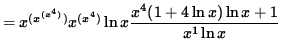
(Divide out a factor of ![]() and combine the powers of x .)
and combine the powers of x .)
![]()
(Combine the powers of x again.)
![]()
Click HERE to return to the list of problems.
.