-
1.)
BOTH OF THESE SOLUTIONS ARE WRONG because the ordinary rules of differentiation do not apply. Logarithmic differentiation will provide a way to differentiate a function of this type. It requires deft algebra skills and careful use of the following unpopular, but well-known, properties of logarithms. Though the following properties and methods are true for a logarithm of any base, only the natural logarithm (base e, where e
![]() ),
), ![]() , will be used in this problem set.
, will be used in this problem set.
PROPERTIES OF THE NATURAL LOGARITHM
1. ![]() .
.
2. ![]() .
.
3.
![]() .
.
4.
![]() .
.
5.
![]() .
.
6.
![]() .
.
AVOID THE FOLLOWING LIST OF COMMON MISTAKES
1.
![]() .
.
2.
![]() .
.
3.
![]() .
.
4.
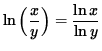 .
.
5.
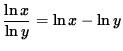 .
.
The following problems range in difficulty from average to challenging.
Click HERE to see a detailed solution to problem 1.
Click HERE to see a detailed solution to problem 2.
Click HERE to see a detailed solution to problem 3.
Click HERE to see a detailed solution to problem 4.
Click HERE to see a detailed solution to problem 5.
Click HERE to see a detailed solution to problem 6.
Click HERE to see a detailed solution to problem 7.
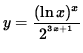 .
.
Click HERE to see a detailed solution to problem 8.
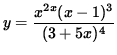 .
.
Click HERE to see a detailed solution to problem 9.
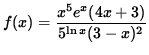 . Find an equation of the line tangent to the graph of f at x=1 .
. Find an equation of the line tangent to the graph of f at x=1 .
Click HERE to see a detailed solution to problem 10.
Click HERE to see a detailed solution to problem 11.
Click HERE to see a detailed solution to problem 12.
Your comments and suggestions are welcome. Please e-mail any correspondence to Duane Kouba by clicking on the following address :