SOLUTION 1 : Because a variable is raised to a variable power in this function, the ordinary rules of differentiation DO NOT APPLY ! The function must first be revised before a derivative can be taken. Begin with
y = xx .
Apply the natural logarithm to both sides of this equation getting
![]()
![]() .
.
Differentiate both sides of this equation. The left-hand side requires the chain rule since y represents a function of x . Use the product rule on the right-hand side. Thus, beginning with
![]()
and differentiating, we get
![]()
![]() .
.
Multiply both sides of this equation by y, getting
![]() .
.
Click HERE to return to the list of problems.
SOLUTION 2 : Because a variable is raised to a variable power in this function, the ordinary rules of differentiation DO NOT APPLY ! The function must first be revised before a derivative can be taken. Begin with
y = x(ex) .
Apply the natural logarithm to both sides of this equation getting
![]()
![]() .
.
Differentiate both sides of this equation. The left-hand side requires the chain rule since y represents a function of x . Use the product rule on the right-hand side. Thus, beginning with
![]()
and differentiating, we get
![]()
(Get a common denominator and combine fractions on the right-hand side.)
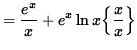
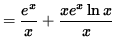
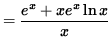
(Factor out ex in the numerator.)
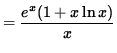 .
.
Multiply both sides of this equation by y, getting
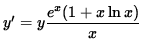
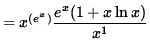
(Combine the powers of x .)
![]() .
.
Click HERE to return to the list of problems.
SOLUTION 3 : Because a variable is raised to a variable power in this function, the ordinary rules of differentiation DO NOT APPLY ! The function must first be revised before a derivative can be taken. Begin with
y = (3x2+5)1/x .
Apply the natural logarithm to both sides of this equation getting
![]()
![]()
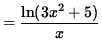 .
.
Differentiate both sides of this equation. The left-hand side requires the chain rule since y represents a function of x . Use the quotient rule and the chain rule on the right-hand side. Thus, beginning with
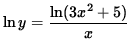
and differentiating, we get
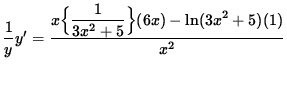
(Get a common denominator and combine fractions in the numerator.)
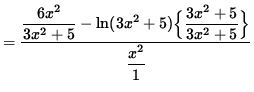
(Dividing by a fraction is the same as multiplying by its reciprocal.)
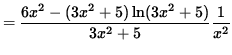
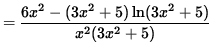 .
.
Multiply both sides of this equation by y, getting
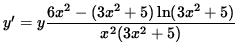
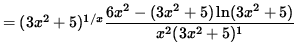
(Combine the powers of (3x2+5) .)
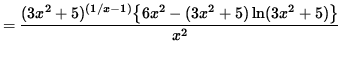 .
.
Click HERE to return to the list of problems.
SOLUTION 4 : Because a variable is raised to a variable power in this function, the ordinary rules of differentiation DO NOT APPLY ! The function must first be revised before a derivative can be taken. Begin with
![]() .
.
Apply the natural logarithm to both sides of this equation getting
![]()
![]() .
.
Differentiate both sides of this equation. The left-hand side requires the chain rule since y represents a function of x . Use the product rule and the chain rule on the right-hand side. Thus, beginning with
truein
![]()
and differentiating, we get
![]()
(Get a common denominator and combine fractions on the right-hand side.)
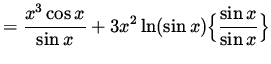
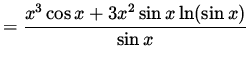 .
.
Multiply both sides of this equation by y, getting
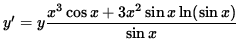
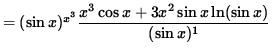
(Combine the powers of ![]() .)
.)
![]() .
.
Click HERE to return to the list of problems.
SOLUTION 5 : Because a variable is raised to a variable power in this function, the ordinary rules of differentiation DO NOT APPLY ! The function must first be revised before a derivative can be taken. Begin with
![]() .
.
Apply the natural logarithm to both sides of this equation and use the algebraic properties of logarithms, getting
![]()
![]()
![]() .
.
Differentiate both sides of this equation. The left-hand side requires the chain rule since y represents a function of x . Use the product rule and the chain rule on the right-hand side. Thus, beginning with
![]()
and differentiating, we get
![]()
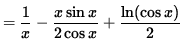
(Get a common denominator and combine fractions on the right-hand side.)
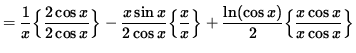
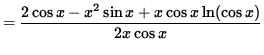 .
.
Multiply both sides of this equation by y, getting
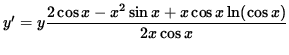
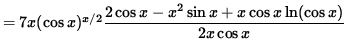
(Divide out a factor of x .)
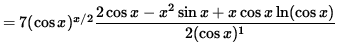
(Combine the powers of ![]() .)
.)
![]() .
.
Click HERE to return to the list of problems.
SOLUTION 6 : Because a variable is raised to a variable power in this function, the ordinary rules of differentiation DO NOT APPLY ! The function must first be revised before a derivative can be taken. Begin with
![]() .
.
Apply the natural logarithm to both sides of this equation and use the algebraic properties of logarithms, getting
![]()
![]()
![]()
![]()
![]() .
.
Differentiate both sides of this equation. The left-hand side requires the chain rule since y represents a function of x . Use the product rule and the chain rule on the right-hand side. Thus, beginning with
![]()
and differentiating, we get
![]()
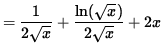
(Get a common denominator and combine fractions on the right-hand side.)
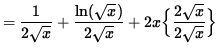
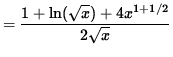
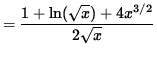 .
.
Multiply both sides of this equation by y, getting
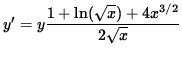
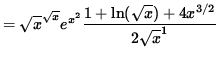
(Combine the powers of ![]() .)
.)
![]() .
.
Click HERE to return to the list of problems.
SOLUTION 7 : Because a variable is raised to a variable power in this function, the ordinary rules of differentiation DO NOT APPLY ! The function must first be revised before a derivative can be taken. Begin with
![]() .
.
Apply the natural logarithm to both sides of this equation and use the algebraic properties of logarithms, getting
![]()
![]()
![]()
![]() .
.
Differentiate both sides of this equation. The left-hand side requires the chain rule since y represents a function of x . Use the product rule and the chain rule on the right-hand side. Thus, beginning with
![]()
and differentiating, we get
![]()
(Divide out a factor of ![]() .)
.)
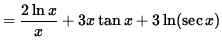
(Get a common denominator and combine fractions on the right-hand side.)
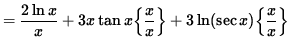
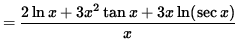 .
.
Multiply both sides of this equation by y, getting
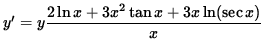
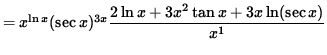
(Combine the powers of x .)
![]()
Click HERE to return to the list of problems.
.