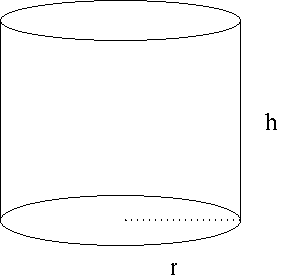
SOLUTION 8 : Let variable r be the radius of the circular base and variable h the height of the cylinder.

The total volume of the cylinder is given to be
![]() (area of base) (height)
(area of base) (height)
![]() ,
,
so that
![]()
![]() .
.
We wish to MINIMIZE the total COST of construction of the cylinder
C = (total cost of bottom) + (total cost of top) + (total cost of side)
= (unit cost of bottom)(area of bottom) + (unit cost of top)(area of top) + (unit cost of side) (area of side)
![]()
(For convenience drop the ![]() signs until the end of the problem.)
signs until the end of the problem.)
![]() .
.
However, before we differentiate the right-hand side, we will write it as a function of r only. Substitute for h getting
![]()
![]()
![]() .
.
Now differentiate this equation, getting
![]()
![]()
(Get a common denominator and combine fractions.)
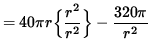
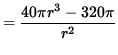
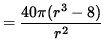
= 0 ,
so that (If
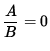 , then A=0 .)
, then A=0 .)
![]() ,
,
r3 = 8 ,
or
r = 2 .
Since variable r measures a distance, it must satisfy r > 0 . See the adjoining sign chart for C' .
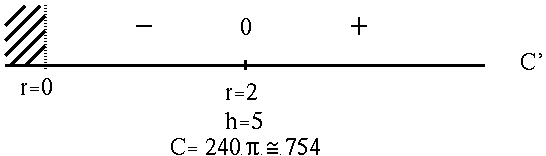
If
r=2 m. and h=5 m. ,
then
![]()
is the least possible cost of construction.
Click HERE to return to the list of problems.
SOLUTION 9 : Let variable x be the distance denoted in the given diagram.
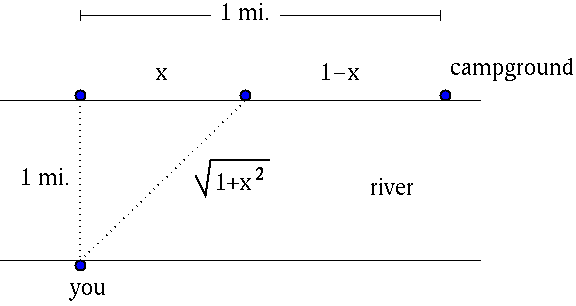
Assume that you travel at the following rates :
SWIM : 2 mph
WALK : 3 mph .
Recall that if travel is at a CONSTANT rate of speed, then
(distance traveled) = (rate of travel) (time elapsed)
or
D = R T ,
so that time elapsed is
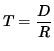 .
.
We wish to MINIMIZE the total TIME elapsed
T = (swim time) + (walk time)
= (swim distance)/(swim rate) + (walk distance)/(walk rate)
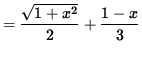
![]() .
.
Now differentiate this equation, getting
![]()
![]()
= 0 ,
so that
![]()
and
![]() .
.
Square both sides of this equation, getting
9x2 = 4 (1 + x2) = 4 + 4x2 ,
so that
5x2 = 4 ,
x2 = 4/5 ,
or
![]() .
.
But
![]() since variable x measures a distance and
since variable x measures a distance and
![]() . See the adjoining sign chart for T' .
. See the adjoining sign chart for T' .
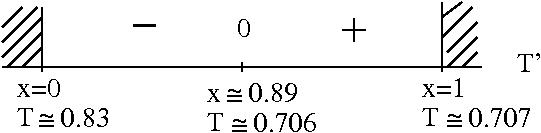
If
![]() mi.
mi.
then
![]() hr.
hr.
is the shortest possible time of travel.
Click HERE to return to the list of problems.
SOLUTION 10 : Let variable x be the width and variable y the length of the rectangular portion of the window.
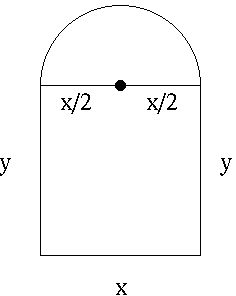
The semi-circular portion of the window has length
(1/2)(Circumference) = (1/2)(2(pi)(radius))= (1/2)(2(pi)(x/2))= (pi/2)x
The perimeter (distance around outside only) of the window is given to be
12 = x + 2y + (pi/2)x
so that
2y = 12 - x - (pi/2)x
or
y = 6 - (1/2)x - (pi/4)x
We wish to MAXIMIZE the total AREA of the RECTANGLE
A = (width) (length) = x y .
However, before we differentiate the right-hand side, we will write it as a function of x only. Substitute for y getting
A = x y
![]()
![]() .
.
Now differentiate this equation, getting
![]()
![]()
= 0
for
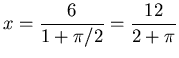 ,
,
i.e.,
![]() .
.
Since variable x measures distance, ![]() . In addition, x is largest when y = 0 and the window is in the shape of a semi-circle. Thus,
. In addition, x is largest when y = 0 and the window is in the shape of a semi-circle. Thus,
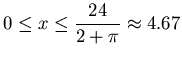 (Why ?).
See the adjoining sign chart for A' .
(Why ?).
See the adjoining sign chart for A' .
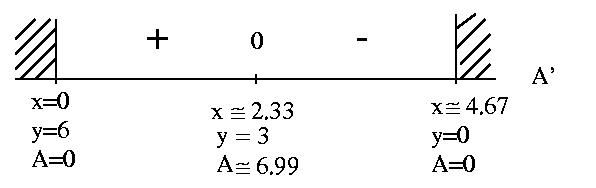
If
![]() ft. and y=3 ft. ,
ft. and y=3 ft. ,
then
![]() ft.2
ft.2
is the largest possible area of the rectangle.
Click HERE to return to the list of problems.
SOLUTION 11 : Let variable x be the ADDITIONAL trees planted in the existing orchard. We wish to MAXIMIZE the total PRODUCTION of apples
P = (number of trees) (apple output per tree)
= ( 50 + x ) ( 800 - 10x )
= 40,000 + 300 x - 10 x2 .
Now differentiate this equation, getting
P' = 300 - 20 x
= 20 ( 15 - x )
= 0
for
x=15 .
See the adjoining sign chart for P' .
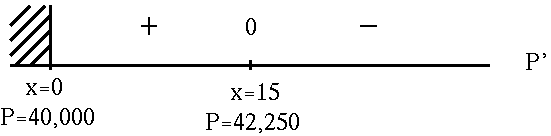
If
x = 15 additional trees ,
then
P = 42,250 apples
is the largest possible production of apples.
Click HERE to return to the list of problems.
SOLUTION 12 : Let variable x be the length of the base and variable y the height of the inscribed rectangle.
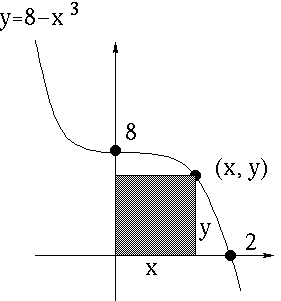
We wish to MAXIMIZE the total AREA of the rectangle
A = (length of base) (height) = xy .
However, before we differentiate the right-hand side, we will write it as a function of x only. Substitute for y getting
A = x y
= x ( 8 - x3 )
= 8x - x4 .
Now differentiate this equation, getting
A' = 8 - 4 x3
= 4 ( 2 - x3 )
= 0 ,
so that
x3 = 2
and
![]() .
.
Note that
![]() . See the adjoining sign chart for A' .
. See the adjoining sign chart for A' .
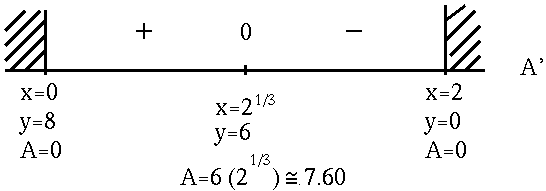
If
![]() and y = 6 ,
and y = 6 ,
then
![]()
is the largest possible area for the inscribed rectangle.
Click HERE to return to the list of problems.
SOLUTION 13 : Let variable r be the length of the base and variable h the height of the rectangle.
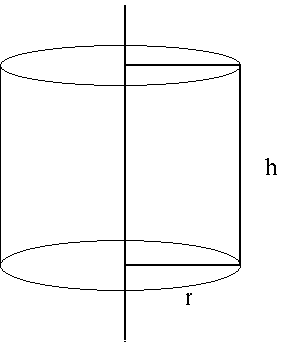
It is given that the perimeter of the rectangle is
12 = 2r + 2h
so that
2h = 12 - 2r
and
h = 6 - r .
We wish to MAXIMIZE the total VOLUME of the resulting CYLINDER
V = (area of base) (height)
![]() .
.
However, before we differentiate the right-hand side, we will write it as a function of r only. Substitute for h getting
![]()
![]()
![]() .
.
Now differentiate this equation, getting
![]()
![]()
![]()
= 0
for
r=0 or r=4 .
Since variable r measures distance and the perimeter of the rectangle is 12,
![]() . See the adjoining sign chart for V' .
. See the adjoining sign chart for V' .
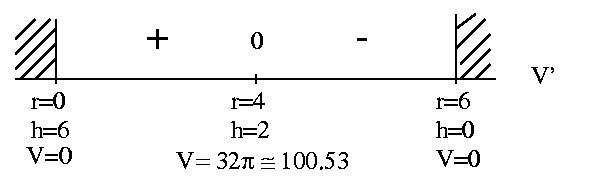
If
r = 4 ft. and h = 2 ft. ,
then
![]() ft.
ft.
![]() ft.3
ft.3
is the largest possible volume for the cylinder.
Click HERE to return to the list of problems.
SOLUTION 14 :
Let variable ![]() be the viewing angle and variable x the distance as denoted in the diagram. We seek to write angle
be the viewing angle and variable x the distance as denoted in the diagram. We seek to write angle ![]() as a function of distance x . Introduce angle
as a function of distance x . Introduce angle ![]() as in the diagram below.
as in the diagram below.
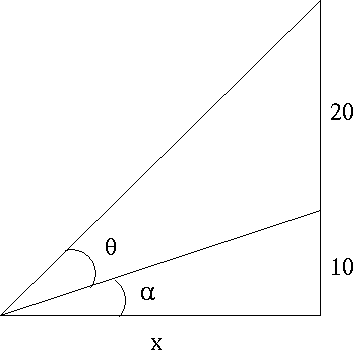
It follows from basic trigonometry that
![]()
so that
(Equation 1)
![]() .
.
In a similar fashion
![]()
so that
![]() ,
,
or
(Equation 2)
![]() .
.
Use ![]() from Equation 1 to substitute into Equation 2, getting
from Equation 1 to substitute into Equation 2, getting
![]() .
.
We wish to MAXIMIZE angle THETA given in this equation. Differentiate this equation, getting
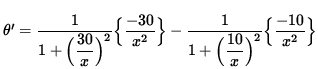
![]()
= 0 ,
so that
![]() ,
,
30 x2 + 3000 = 10 x2 + 9000 ,
20 x2 = 6000 ,
x2 = 300 ,
for
![]() .
.
But
![]() since variable x measures distance and
since variable x measures distance and ![]() . If
. If
![]() , then
, then
![]()
![]()
![]()
(These are well-known values from basic trigonometry.)
![]()
![]() radians
radians
or
![]() degrees .
degrees .
See the adjoining sign chart for ![]() .
.
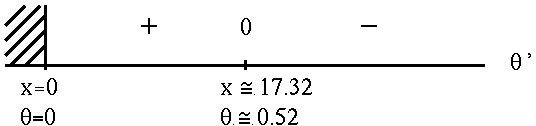
If
![]() ft.
ft.
![]() ft.
ft.
then
![]() degrees
degrees
![]() radians
radians
is the largest possible viewing angle.
Click HERE to return to the list of problems.