- PROBLEM 1 : Find two nonnegative numbers whose sum is 9 and so that the product of one number and the square of the other number is a maximum.
Click HERE to see a detailed solution to problem 1.
- PROBLEM 2 : Build a rectangular pen with three parallel partitions using 500 feet of fencing. What dimensions will maximize the total area of the pen ?
Click HERE to see a detailed solution to problem 2.
- PROBLEM 3 : An open rectangular box with square base is to be made from 48 ft.2 of material. What dimensions will result in a box with the largest possible volume ?
Click HERE to see a detailed solution to problem 3.
- PROBLEM 4 : A container in the shape of a right circular cylinder with no top has surface area 3
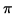 ft.2 What height h and base radius r will maximize the volume of the cylinder ?
ft.2 What height h and base radius r will maximize the volume of the cylinder ?
Click HERE to see a detailed solution to problem 4.
- PROBLEM 5 : A sheet of cardboard 3 ft. by 4 ft. will be made into a box by cutting equal-sized squares from each corner and folding up the four edges. What will be the dimensions of the box with largest volume ?
Click HERE to see a detailed solution to problem 5.
- PROBLEM 6 : Consider all triangles formed by lines passing through the point (8/9, 3) and both the x- and y-axes. Find the dimensions of the triangle with the shortest hypotenuse.
Click HERE to see a detailed solution to problem 6.
- PROBLEM 7 : Find the point (x, y) on the graph of
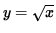 nearest the point (4, 0).
nearest the point (4, 0).
Click HERE to see a detailed solution to problem 7.
- PROBLEM 8 : A cylindrical can is to hold 20
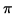 m.3 The material for the top and bottom costs $10/m.2 and material for the side costs $8/m.2 Find the radius r and height h of the most economical can.
m.3 The material for the top and bottom costs $10/m.2 and material for the side costs $8/m.2 Find the radius r and height h of the most economical can.
Click HERE to see a detailed solution to problem 8.
- PROBLEM 9 : You are standing at the edge of a slow-moving river which is one mile wide and wish to return to your campground on the opposite side of the river. You can swim at 2 mph and walk at 3 mph. You must first swim across the river to any point on the opposite bank. From there walk to the campground, which is one mile from the point directly across the river from where you start your swim. What route will take the least amount of time ?
Click HERE to see a detailed solution to problem 9.
- PROBLEM 10 : Construct a window in the shape of a semi-circle over a rectangle. If the distance around the outside of the window is 12 feet, what dimensions will result in the rectangle having largest possible area ?
Click HERE to see a detailed solution to problem 10.
- PROBLEM 11 : There are 50 apple trees in an orchard. Each tree produces 800 apples. For each additional tree planted in the orchard, the output per tree drops by 10 apples. How many trees should be added to the existing orchard in order to maximize the total output of trees ?
Click HERE to see a detailed solution to problem 11.
- PROBLEM 12 : Find the dimensions of the rectangle of largest area which can be inscribed in the closed region bounded by the x-axis, y-axis, and graph of y=8-x3 . (See diagram.)
Click HERE to see a detailed solution to problem 12.
- PROBLEM 13 : Consider a rectangle of perimeter 12 inches. Form a cylinder by revolving this rectangle about one of its edges. What dimensions of the rectangle will result in a cylinder of maximum volume ?
Click HERE to see a detailed solution to problem 13.
- PROBLEM 14 : A movie screen on a wall is 20 feet high and 10 feet above the floor. At what distance x from the front of the room should you position yourself so that the viewing angle
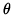 of the movie screen is as large as possible ? (See diagram.)
of the movie screen is as large as possible ? (See diagram.)
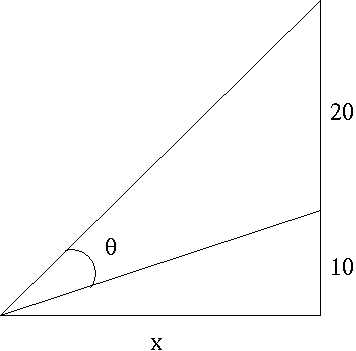
Click HERE to see a detailed solution to problem 14.
- PROBLEM 15 : Find the dimensions (radius r and height h) of the cone of maximum volume which can be inscribed in a sphere of radius 2.
Click HERE to see a detailed solution to problem 15.
- PROBLEM 16 : What angle
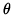 between two edges of length 3 will result in an isosceles triangle with the largest area ? (See diagram.)
between two edges of length 3 will result in an isosceles triangle with the largest area ? (See diagram.)
Click HERE to see a detailed solution to problem 16.
- PROBLEM 17 : Of all lines tangent to the graph of
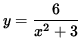 , find the tangent lines of mimimum slope and maximum slope.
, find the tangent lines of mimimum slope and maximum slope.
Click HERE to see a detailed solution to problem 17.
- PROBLEM 18 : Find the length of the shortest ladder that will reach over an 8-ft. high fence to a large wall which is 3 ft. behind the fence. (See diagram.)
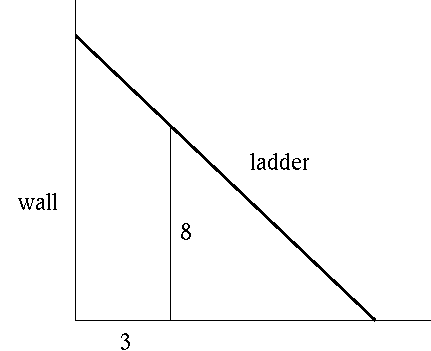
Click HERE to see a detailed solution to problem 18.
- PROBLEM 19 : Find the point P = (x, 0) on the x-axis which minimizes the sum of the squares of the distances from P to (0, 0) and from P to (3, 2).
Click HERE to see a detailed solution to problem 19.
- PROBLEM 20 : Car B is 30 miles directly east of Car A and begins moving west at 90 mph. At the same moment car A begins moving north at 60 mph. What will be the minimum distance between the cars and at what time t does the minimum distance occur ?
Click HERE to see a detailed solution to problem 20.
- PROBLEM 21 : A rectangular piece of paper is 12 inches high and six inches wide. The lower right-hand corner is folded over so as to reach the leftmost edge of the paper (See diagram.).
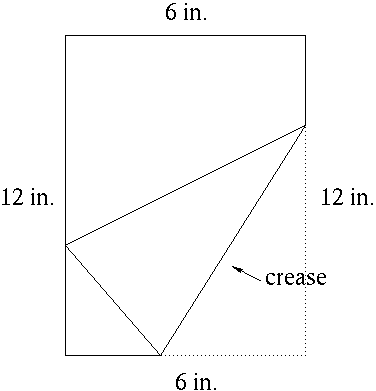
Find the minimum length of the resulting crease.
Click HERE to see a detailed solution to problem 21.