SOLUTION 1 : Let variables x and y represent two nonnegative numbers. The sum of the two numbers is given to be
9 = x + y ,
so that
y = 9 - x .
We wish to MAXIMIZE the PRODUCT
P = x y2 .
However, before we differentiate the right-hand side, we will write it as a function of x only. Substitute for y getting
P = x y2
= x ( 9-x)2 .
Now differentiate this equation using the product rule and chain rule, getting
P' = x (2) ( 9-x)(-1) + (1) ( 9-x)2
= ( 9-x) [ -2x + ( 9-x) ]
= ( 9-x) [ 9-3x ]
= ( 9-x) (3)[ 3-x ]
= 0
for
x=9 or x=3 .
Note that since both x and y are nonnegative numbers and their sum is 9, it follows that
![]() . See the adjoining sign chart for P' .
. See the adjoining sign chart for P' .
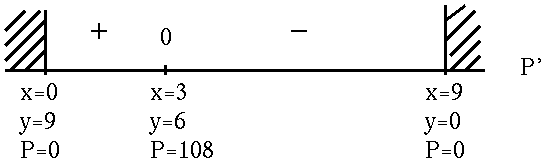
If
x=3 and y=6 ,
then
P= 108
is the largest possible product.
Click HERE to return to the list of problems.
SOLUTION 2 : Let variable x be the width of the pen and variable y the length of the pen.
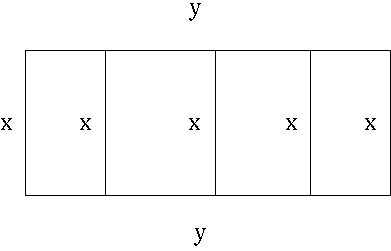
The total amount of fencing is given to be
500 = 5 (width) + 2 (length) = 5x + 2y ,
so that
2y = 500 - 5x
or
y = 250 - (5/2)x .
We wish to MAXIMIZE the total AREA of the pen
A = (width) (length) = x y .
However, before we differentiate the right-hand side, we will write it as a function of x only. Substitute for y getting
A = x y
= x ( 250 - (5/2)x)
= 250x - (5/2)x2 .
Now differentiate this equation, getting
A' = 250 - (5/2) 2x
= 250 - 5x
= 5 (50 - x )
= 0
for
x=50 .
Note that since there are 5 lengths of x in this construction and 500 feet of fencing, it follows that
![]() . See the adjoining sign chart for A' .
. See the adjoining sign chart for A' .
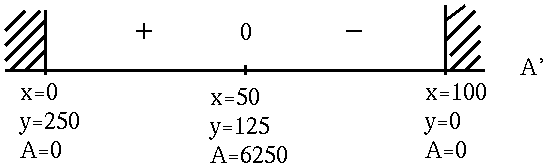
If
x=50 ft. and y=125 ft. ,
then
A = 6250 ft.2
is the largest possible area of the pen.
Click HERE to return to the list of problems.
SOLUTION 3 : Let variable x be the length of one edge of the square base and variable y the height of the box.
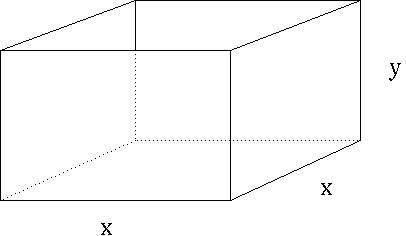
The total surface area of the box is given to be
48 = (area of base) + 4 (area of one side) = x2 + 4 (xy) ,
so that
4xy = 48 - x2
or
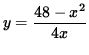
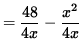
![]() .
.
We wish to MAXIMIZE the total VOLUME of the box
V = (length) (width) (height) = (x) (x) (y) = x2 y .
However, before we differentiate the right-hand side, we will write it as a function of x only. Substitute for y getting
V = x2 y
![]()
= 12x - (1/4)x3 .
Now differentiate this equation, getting
V' = 12 - (1/4)3x2
= 12 - (3/4)x2
= (3/4)(16 - x2 )
= (3/4)(4 - x)(4 + x)
= 0
for
x=4 or x=-4 .
But ![]() since variable x measures a distance and x > 0 . Since the base of the box is square and there are 48 ft.2 of material, it follows that
since variable x measures a distance and x > 0 . Since the base of the box is square and there are 48 ft.2 of material, it follows that
![]() . See the adjoining sign chart for V' .
. See the adjoining sign chart for V' .
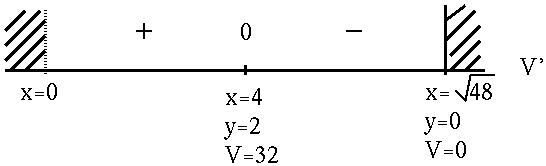
If
x=4 ft. and y=2 ft. ,
then
V = 32 ft.3
is the largest possible volume of the box.
Click HERE to return to the list of problems.
SOLUTION 4 : Let variable r be the radius of the circular base and variable h the height of the cylinder.
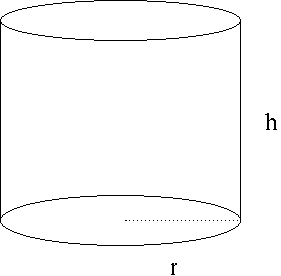
The total surface area of the cylinder is given to be
![]() (area of base) + (area of the curved side)
(area of base) + (area of the curved side)
![]() ,
,
so that
![]()
or
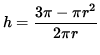
![]() .
.
We wish to MAXIMIZE the total VOLUME of the cylinder
V = (area of base) (height)
![]() .
.
However, before we differentiate the right-hand side, we will write it as a function of r only. Substitute for h getting
![]()
![]()
![]() .
.
Now differentiate this equation, getting
![]()
![]()
![]()
= 0
for
r=1 or r=-1 .
But ![]() since variable r measures a distance and r > 0 . Since the base of the box is a circle and there are
since variable r measures a distance and r > 0 . Since the base of the box is a circle and there are ![]() ft.2 of material, it follows that
ft.2 of material, it follows that
![]() . See the adjoining sign chart for V' .
. See the adjoining sign chart for V' .
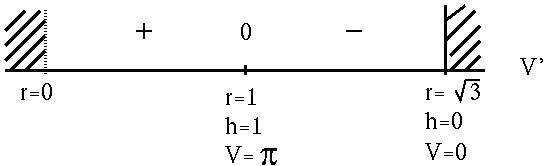
If
r=1 ft. and h=1 ft. ,
then
![]() ft.3
ft.3
is the largest possible volume of the cylinder.
Click HERE to return to the list of problems.
SOLUTION 5 : Let variable x be the length of one edge of the square cut from each corner of the sheet of cardboard.
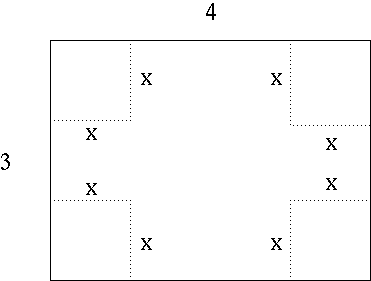
After removing the corners and folding up the flaps, we have an ordinary rectangular box.
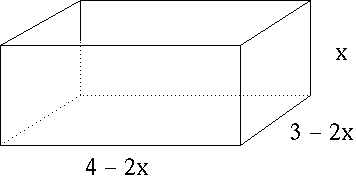
We wish to MAXIMIZE the total VOLUME of the box
V = (length) (width) (height) = (4-2x) (3-2x) (x) .
Now differentiate this equation using the triple product rule, getting
V' = (-2) (3-2x) (x) + (4-2x) (-2) (x) + (4-2x) (3-2x) (1)
= -6x + 4x2 - 8x + 4x2 + 4x2 - 14x + 12
= 12x2 - 28x + 12
= 4 ( 3x2 - 7x + 3 )
= 0
for (Use the quadratic formula.)
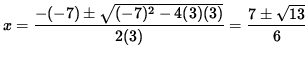 ,
,
i.e., for
![]() or
or
![]() .
.
But
![]() since variable x measures a distance. In addition, the short edge of the cardboard is 3 ft., so it follows that
since variable x measures a distance. In addition, the short edge of the cardboard is 3 ft., so it follows that
![]() . See the adjoining sign chart for V' .
. See the adjoining sign chart for V' .
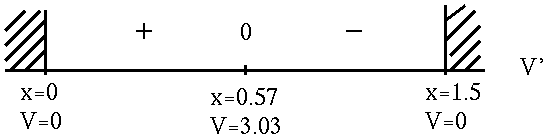
If
![]() ft. ,
ft. ,
then
![]() ft.3
ft.3
is largest possible volume of the box.
Click HERE to return to the list of problems.
SOLUTION 6 : Let variable x be the x-intercept and variable y the y-intercept of the line passing throught the point (8/9, 3) .
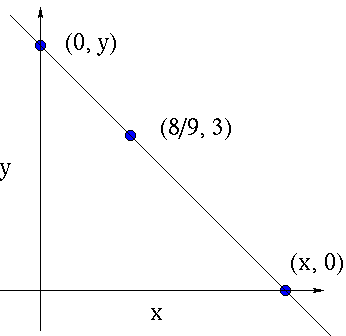
Set up a relationship between x and y using similar triangles.
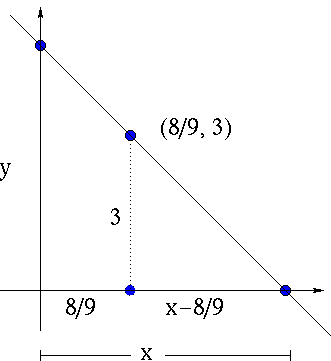
One relationship is
![]() ,
,
so that
![]() .
.
We wish to MINIMIZE the length of the HYPOTENUSE of the triangle
![]() .
.
However, before we differentiate the right-hand side, we will write it as a function of x only. Substitute for y getting
![]()
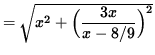 .
.
Now differentiate this equation using the chain rule and quotient rule, getting
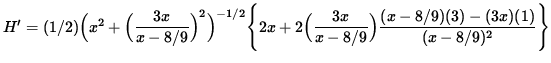
(Factor a 2 out of the big brackets and simplify.)
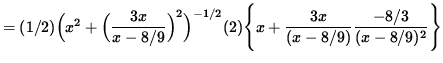
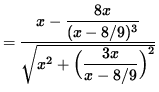
= 0 ,
so that (If
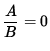 , then A=0 .)
, then A=0 .)
![]() .
.
By factoring out x , it follows that
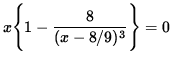 ,
,
so that (If AB= 0 , then A=0 or B=0 .)
x=0
(Impossible, since x> 8/9. Why ?) or
![]() .
.
Then
![]() ,
,
so that
(x-8/9)3 = 8 ,
x-8/9 = 2 ,
and
x = 26/9 .
See the adjoining sign chart for H' .
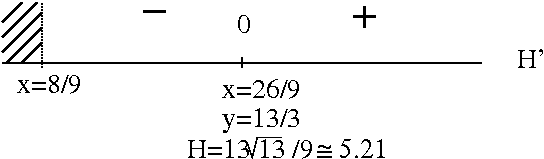
If
x = 26/9 and y=13/3 ,
then
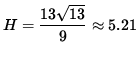
is the shortest possible hypotenuse.
Click HERE to return to the list of problems.
SOLUTION 7 : Let (x, y) represent a randomly chosen point on the graph of
![]() .
.
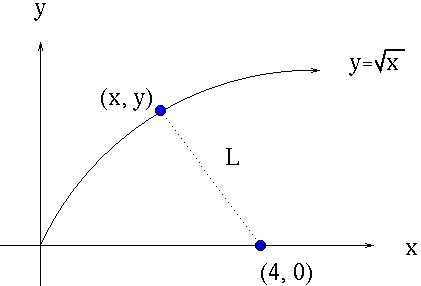
We wish to MINIMIZE the DISTANCE between points (x, y) and (4, 0) ,
![]()
![]() .
.
However, before we differentiate the right-hand side, we will write it as a function of x only. Substitute for y getting
![]()
![]()
![]() .
.
Now differentiate this equation using the chain rule, getting
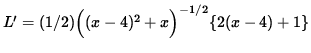
![]()
= 0 ,
so that (If
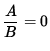 , then A=0 .)
, then A=0 .)
2x-7 = 0 ,
or
x =7/2 .
See the adjoining sign chart for L' .
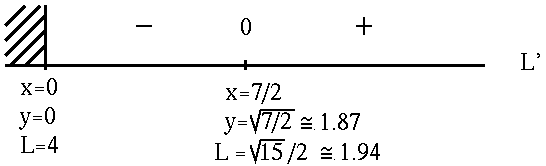
If
x = 7/2 and
![]() ,
,
then
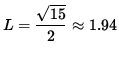
is the shortest possible distance from (4, 0) to the graph of
![]() .
.
Click HERE to return to the list of problems.