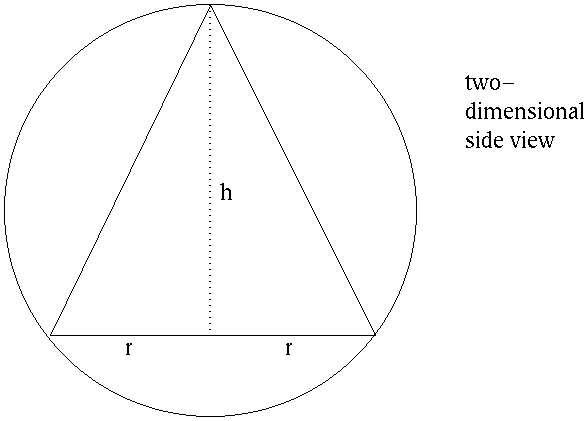
SOLUTION 15 : Let variable r be the radius of the circular base and variable h the height of the inscribed cone as shown in the two-dimensional side view.
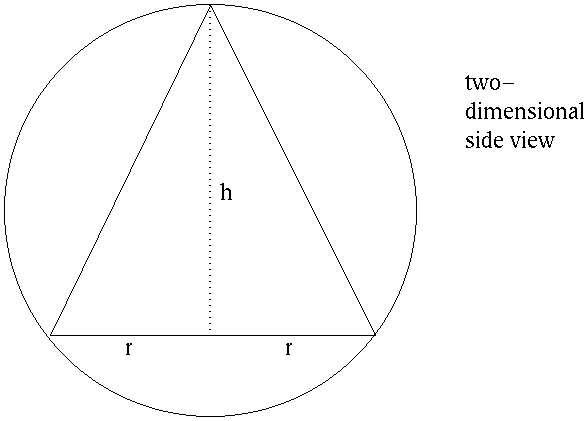
It is given that the circle's radius is 2. Find a relationship between r and h . Let variable z be the height of the small right triangle.
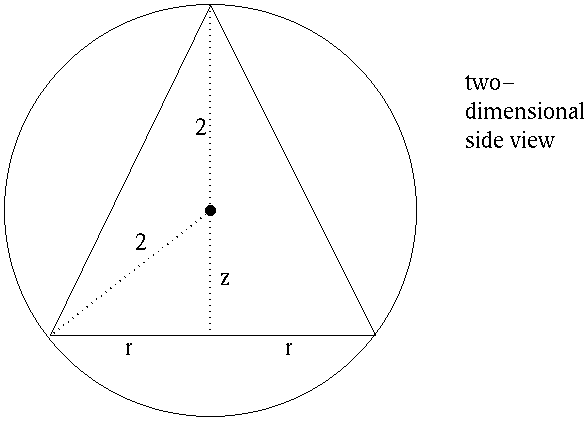
By the Pythagorean Theorem it follows that
r2 + z2 = 22
so that
z2 = 4 - r2
or
![]() .
.
Thus the height of the inscribed cone is
![]() .
.
We wish to MINIMIZE the total VOLUME of the CONE
![]() .
.
However, before we differentiate the right-hand side, we will write it as a function of r only. Substitute for h getting
![]()
![]() .
.
Now differentiate this equation using the product rule and the chain rule, getting
![]()
(Factor out ![]() , get a common denominator, and simplify fractions.)
, get a common denominator, and simplify fractions.)
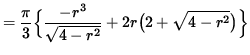
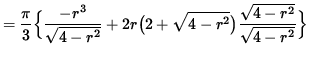
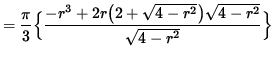
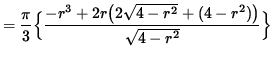
(Factor out (r) .)
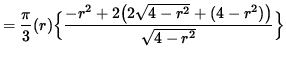
= 0 ,
so that (If AB = 0 , then A=0 or B=0 .)
r = 0
or
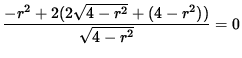 ,
,
i.e., (If
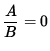 , then A=0 .)
, then A=0 .)
![]() .
.
Then (Isolate the square root term.)
![]() ,
,
![]() ,
,
(Square both sides of this equation.)
![]() ,
,
16 ( 4 - r2 ) = 9 r4 - 48 r2 + 64 ,
64 - 16 r2 = 9 r4 - 48 r2 + 64 ,
32 r2 - 9 r4 = 0 ,
r2 ( 32 - 9 r2 ) = 0 ,
so that
r = 0
or
32 - 9 r2 = 0 ,
r2 = 32/9 ,
or
![]() .
.
But
![]() since variable r measures a distance and
since variable r measures a distance and
![]() . See the adjoining sign chart for V' .
. See the adjoining sign chart for V' .
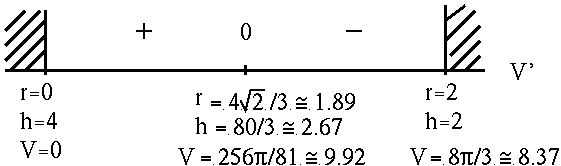
If
![]() and
and
![]() ,
,
then
![]()
is the largest possible volume for the inscribed cone.
Click HERE to return to the list of problems.
SOLUTION 16 : Write the area of the given isosceles triangle as a function of ![]() . Let variable x be the length of the base and variable y the height of the triangle, and consider angle
. Let variable x be the length of the base and variable y the height of the triangle, and consider angle ![]() . Write each of x and y as functions of
. Write each of x and y as functions of ![]() .
.
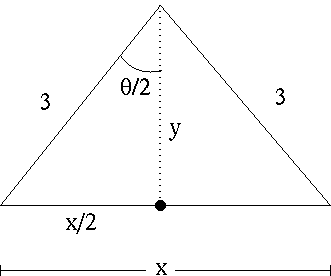
It follows from basic trigonometry that
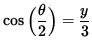
so that
(Equation 1 )
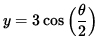 ,
,
and
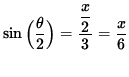
so that
(Equation 2 )
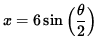
We wish to MAXIMIZE the AREA of the isosceles triangle
A = (1/2) (length of base) (height) = (1/2) xy .
Before we differentiate, use Equations 1 and 2 to rewrite the right-hand side as a function of ![]() only. Then
only. Then
A = (1/2) xy
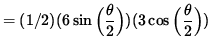
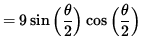 .
.
Now differentiate this equation using the product rule and chain rule, getting
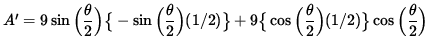
(Factor out (9/2) and simplify the expression.)
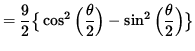
= 0 ,
so that
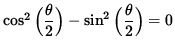
and
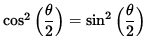 .
.
It follows algebraically (Why ?) that
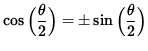
so that from basic trigonometry we get
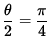 or
or
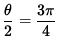 ,
,
and hence
![]() or
or
![]() .
.
Because ![]() measures an angle in a triangle, it is logical to assume that
measures an angle in a triangle, it is logical to assume that
![]() .
Thus,
.
Thus,
![]() . See the adjoining sign chart for A' .
. See the adjoining sign chart for A' .
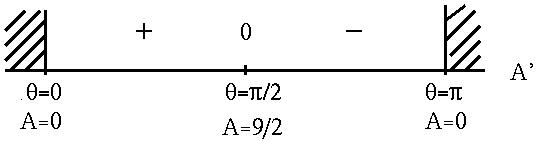
If
![]() radians = 90 degrees,
radians = 90 degrees,
then
A = 9/2
is the largest possible area for the triangle.
Click HERE to return to the list of problems.
SOLUTION 17 : We need to determine a general SLOPE EQUATION for tangent lines.
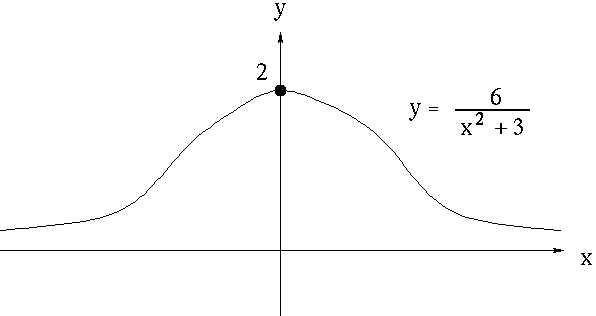
This means that we need the first derivative of y . Differentiate
![]() using the quotient rule, getting
using the quotient rule, getting
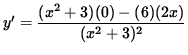
![]() .
.
We wish to MAXIMIZE and MINIMIZE the SLOPE equation
![]() .
.
Now differentiate this equation using the quotient rule and chain rule, getting
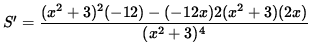
(Factor out -12 and (x2+3) from the numerator and simplify the expression.)
![$ = \displaystyle{ -12 (x^2 + 3) [ (x^2 + 3) - 4x^2 ]\over (x^2 + 3)^4 } $](img48.gif)
(Divide out a factor of (x2+3) .)
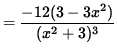
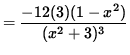
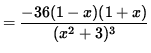
= 0 ,
so that (If
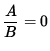 , then A = 0 .)
, then A = 0 .)
-36 ( 1 - x ) ( 1 + x ) = 0
and (If AB = 0 , then A = 0 or B = 0 .)
x=1 or x=-1 .
See the adjoining sign chart for S' .

If
x=-1 and y = 3/2 ,
then
S= 3/4
is the largest possible slope for this graph. The corresponding tangent line is
y - 3/2 = 3/4( x - (-1) )
or
y = (3/4)x + (9/4) .
If
x=1 and y = 3/2 ,
then
S= -3/4
is the smallest possible slope for this graph. The corresponding tangent line is
y - 3/2 = -3/4( x - 1 )
or
y = (-3/4)x + (9/4) .
Click HERE to return to the list of problems.
SOLUTION 18 : Let variable L be the length of the ladder resting on the top of the fence and touching the wall behind it. Let variables x and y be the lengths as shown in the diagram.
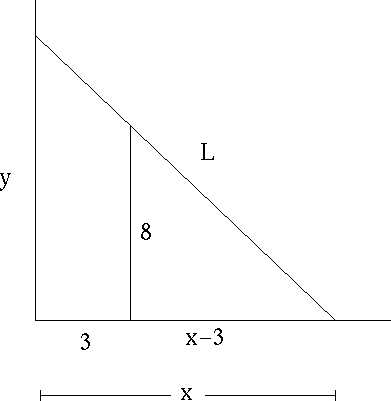
Write L as a function of x . First find a relationship between y and x using similar triangles. For example,
![]()
so that
![]() .
.
We wish to MINIMIZE the LENGTH of the ladder
![]() .
.
Before we differentiate, rewrite the right-hand side as a function of x only. Then
![]()
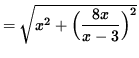
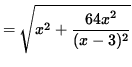 .
.
Now differentiate this equation using the chain rule and quotient rule, getting
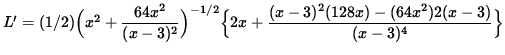
(Factor out 64x and (x-3) from the numerator of the fraction inside the brackets.)
![$ = (1/2) \Big( x^2 + \displaystyle{ 64x^2 \over (x-3)^2 } \Big)^{-1/2}
\Big\{ 2x + \displaystyle{64x(x-3) [ 2(x-3) - 2x ] \over (x-3)^4 } \Big\} $](img58.gif)
(Divide out a factor of (x-3) and simplify the entire expression.)
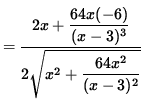
(Factor out 2x from the numerator.)
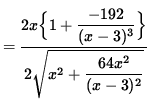
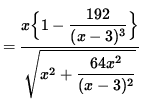
= 0 ,
so that (If
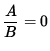 , then A = 0 .)
, then A = 0 .)
![]() .
.
Then (If AB = 0 , then A = 0 or B = 0 .)
x=0
or
![]() ,
,
so that
![]() ,
,
(x-3)3 = 192 ,
![]() ,
,
and
![]() .
.
Note that x > 3 . See the adjoining sign chart for L' .
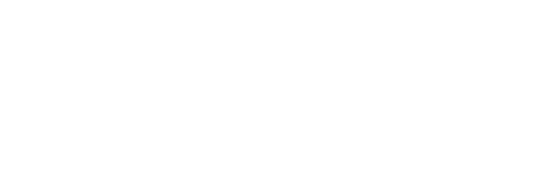
If
![]() ft.
and
ft.
and
![]() ft.
,
ft.
,
then
![]() ft.
ft.
is the length of the shortest possible ladder.
Click HERE to return to the list of problems.
Let variable S be the sum of the squares of the distances between (0, 0) and (x, 0) ,
![]() ,
,
and between (3, 2) and (x, 0) ,
![]() .
.
We wish to MINIMIZE the SUM of the squares of the distances
S = x2 + ( x2 -6x +13 ) = 2x2 -6x +13 .
Now differentiate, getting
S' = 4x -6
= 4(x - 3/2)
= 0
for
x= 3/2 .
See the adjoining sign chart for S' .
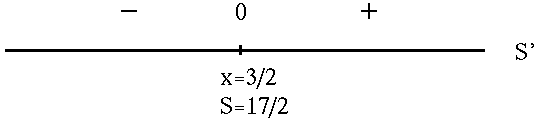
If
x = 3/2 ,
then
S = 17/2
is the smallest sum.
Click HERE to return to the list of problems.
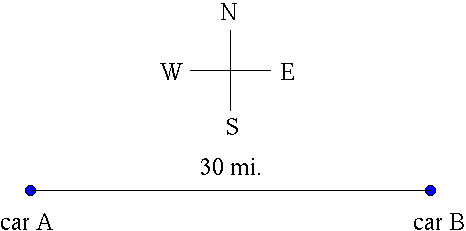
Assume that the two cars travel at the following rates :
CAR A : 60 mph
CAR B : 90 mph
Let variable x be the distance car A travels in t hours, and variable y the distance car B travels in t hours. Let variable L be the distance between cars A and B after t hours.
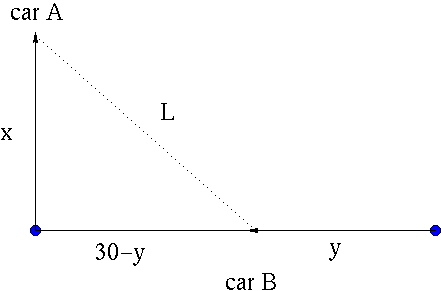
Thus, by the Pythagorean Theorem distance L is
![]() .
.
Before we differentiate, we will rewrite the right-hand side as a function of t only. Recall that if travel is at a CONSTANT rate then
(distance traveled) = (rate of travel) (time elapsed) .
Thus, for car A the distance traveled after t hours is
(Equation 1 )
x = 60 t ,
and for car B the distance traveled after t hours is
(Equation 2 )
y = 90 t .
Use Equations 1 and 2 to rewrite the equation for L as a function of t only. Thus, we wish to MINIMIZE the DISTANCE between the two cars
![]()
![]()
![]() .
.
Differentiate, using the chain rule, getting
![]()
![]()
= 0
so that (If
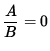 , then A = 0 .)
, then A = 0 .)
23,400 t - 5400 = 0 ,
and
![]() .
.
See the adjoining sign chart for L' .
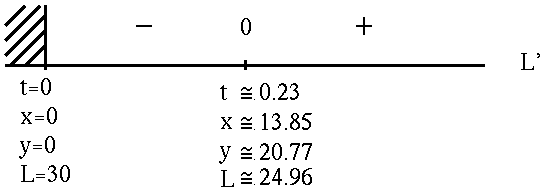
If
![]() hrs. = 13.8 min. ,
hrs. = 13.8 min. ,
then
![]() mi. ,
mi. ,
![]() mi. ,
mi. ,
and
![]() mi.
mi.
is the shortest possible distance between the cars.
Click HERE to return to the list of problems.
SOLUTION 21 : Let variable L represent the length of the crease and let variables x and y be as shown in the diagram.
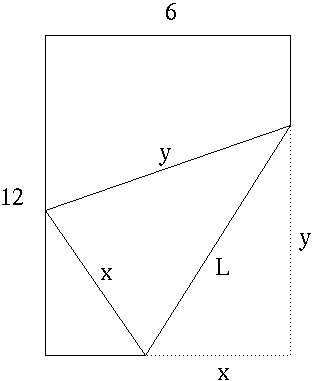
We wish to write L as a function of x . Introduce variable w as shown in the following diagram.
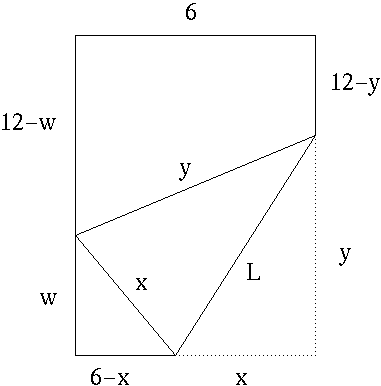
It follows from the Pythagorean Theorem that
w2 + (6-x)2 = x2 ,
so that
w2 = x2 - (x2 - 12x + 36) = 12x - 36
and
![]() .
.
Find a relationship between x and y . The total area of the paper can be computed from the areas of three right triangles, two of which are exactly the same dimensions, and one rhombus. In particular
72 = (total area of paper)
= (area of small triangle) + 2(area of large triangle) + (area of rhombus)
= (1/2)(length of base)(height) + 2(1/2)(length of base)(height) + (average height)(length of base)
![]()
![]()
![]()
![]() ,
,
i.e.,
![]() .
.
Solve this equation for y . Then
![]() ,
,
![]() ,
,
![]() ,
,
and
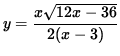 .
.
We wish to MINIMIZE the LENGTH of the crease
![]() .
.
Before we differentiate, rewrite the right-hand side as a function of x only. Then
![]()
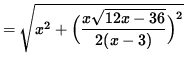
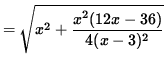
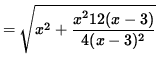
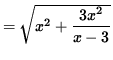 .
.
Now differentiate this equation using the chain rule and quotient rule, getting
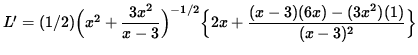
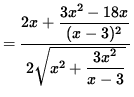
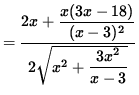
(Factor out x from the numerator.)
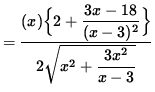
= 0 ,
so that (If
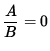 , then A = 0 .)
, then A = 0 .)
![]() .
.
Thus, (If AB = 0 , then A = 0 or B = 0 .)
x = 0
or
![]() ,
,
![]() ,
,
-2 (x-3)2 = 3x - 18 ,
-2 (x2 - 6x + 9) = 3x - 18 ,
-2 x2 + 12x -18 = 3x - 18 ,
-2 x2 + 9x = 0 ,
x ( -2x + 9 ) = 0 ,
so that (If AB = 0 , then A = 0 or B = 0 .)
x = 0
or
( -2x + 9 ) = 0 ,
i.e.,
x = 9/2 .
Note that since the paper is 6 inches wide, it follows that
![]() . See the adjoining sign chart for L' .
. See the adjoining sign chart for L' .
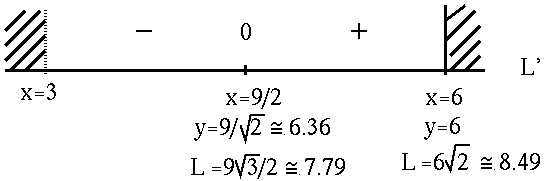
If
x = 9/2 in. and
![]() in.
in.
![]() in. ,
in. ,
then
![]() in.
in.
![]() in.
in.
is the length of the shortest possible crease.
Click HERE to return to the list of problems.