Solving Problems Using Newton's Method
Solving algebraic equations is a common exercise in introductory Mathematics classes. However, sometimes equations cannot be solved using simple algebra and we might be required to find a good, accurate $ estimate $ of the exact solution. A common and easily used algorithm to find a good estimate to an equation's exact solution is
Newton's Method (also called the Newton-Raphson Method), which was developed in the late 1600's by the English Mathematicians Sir Isaac Newton and
Joseph Raphson .
The algorithm for Newton's Method is simple and easy-to-use. It uses the the first derivative of a function and is based on the basic Calculus concept that the derivative
of a function $ f $ at $x=c$ is the slope of the line tangent to the graph of $y=f(x)$ at the point $ (c, f(c)) $. Let's carefully construct Newton's Method.
Let $ y=f(x) $ be a differentiable function. Our goal is to solve the equation $ f(x)=0 $ for $x$. Let's call the exact solution to this equation $x=r$. See the diagram below.
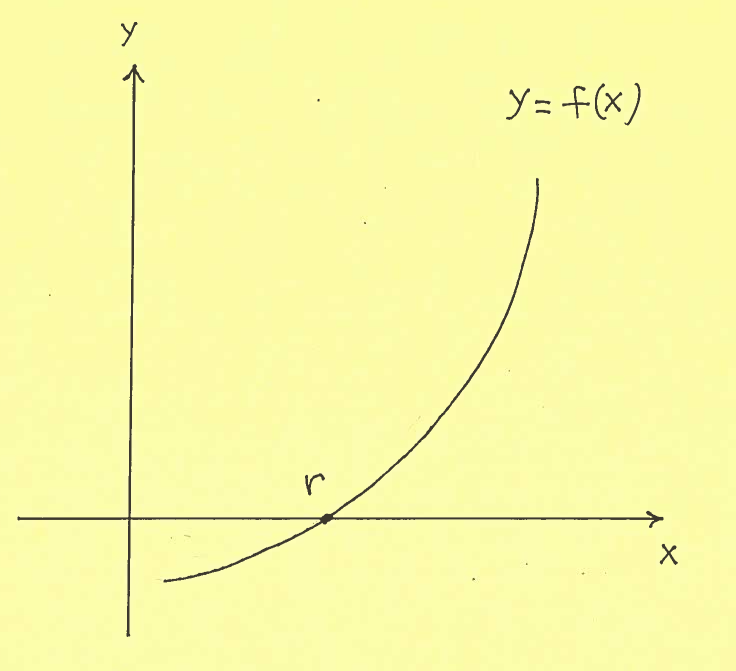
We begin with an $ initial \ guess $ $x_{0}$. At the point $ (x_{0}, f(x_{0})) $ draw the tangent line. Denote $x_{1}$ as the point where this tangent line crosses the $x$-axis. The point $x_{1}$ is our second guess. Repeat. At the point $ (x_{1}, f(x_{1})) $ draw the tangent line. Denote $x_{2}$ as the point where this tangent line crosses the $x$-axis. The point $x_{2}$ is our third guess. Repeat ... etc. See the diagram below.
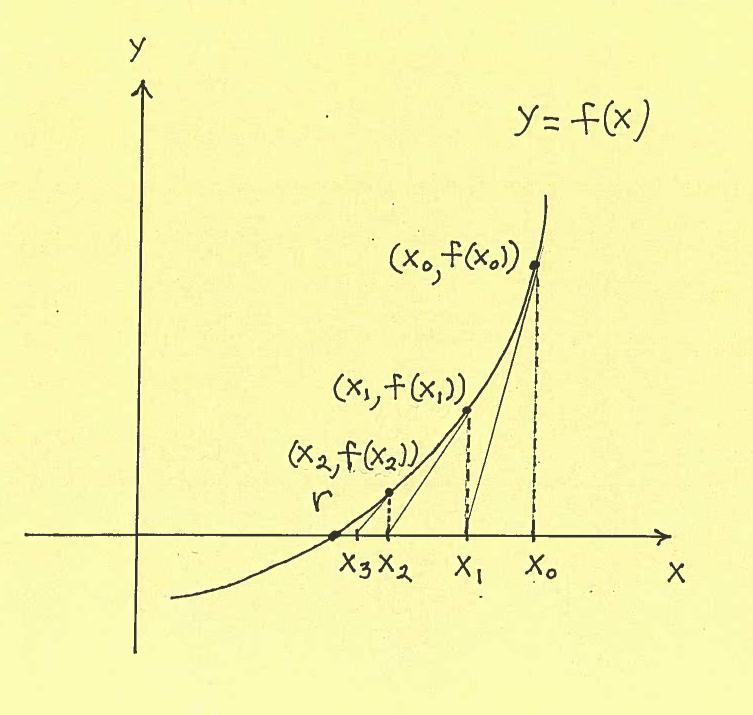
We can see that these successive guesses, $ \ x_{0}, x_{1}, x_{2}, x_{3}, \cdots \ $ zig-zag their way and get closer and closer to the exact solution $x=r$. Let's create a $ recursion $ which will generate a sequence of successive guesses. Let's first consider how we can go from one guess to the next, i.e., from guess $ x_{n} $ to guess $ x_{n+1} $. See the diagram below.
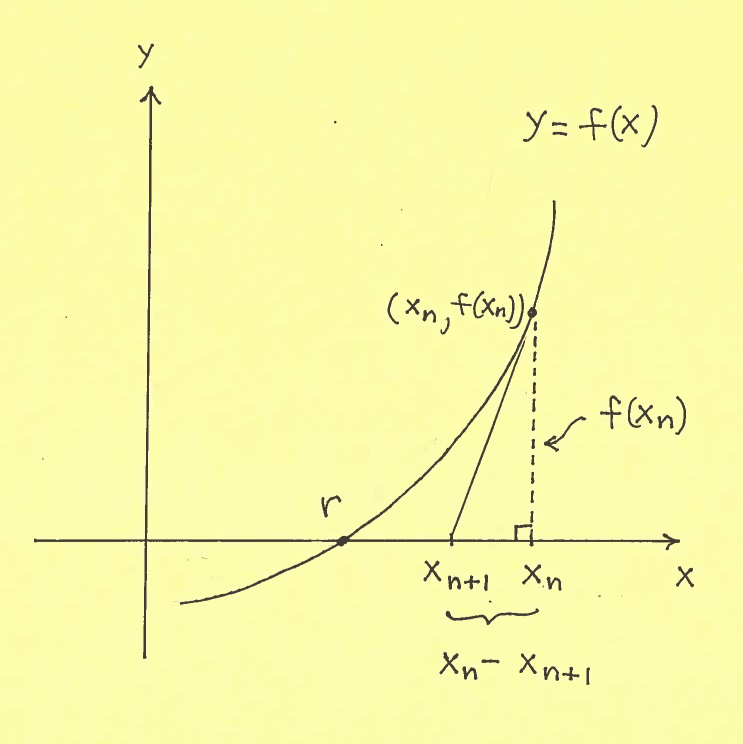
The $ SLOPE $ of the tangent line at the point $ (x_{n}, f(x_{n})) $ is
$$ I.) \ \ \ m = f'(x_{n}) $$
and
$$ II.) \ \ \ m = \displaystyle{ rise \over run } = { f(x_{n}) \over x_{n} - x_{n+1} } $$
Now set the two slopes equal to each other getting
$$ f'(x_{n}) = { f(x_{n}) \over x_{n} - x_{n+1} } \ \ \ \ \longrightarrow $$
$$ x_{n} - x_{n+1} = { f(x_{n}) \over f'(x_{n})} \ \ \ \ \longrightarrow $$
$$ x_{n+1} = x_{n} - { f(x_{n}) \over f'(x_{n})} \ \ \ \ \longrightarrow $$
i.e.,
the recursion for Newton's Method is
$$ x_{n+1} = x_{n} - { f(x_{n}) \over f'(x_{n})} $$
In the list of Newton's Method Problems which follows, most problems are average and a few are somewhat challenging. I recommend using the
Desmos Graphing Calculator
if you want to graph functions. It's fun and easy to use.
- PROBLEM 1 : Apply Newton's Method to the equation $ x^3+x-5=0 $. Begin with the given initial guess, $ x_{0} $, and find $ x_{1} $ and $ x_{2} $. Then use a spreadsheet or some other technology tool to find the solution to this equation to five decimal places.
a.) Use the initial guess $ x_{0}=0 $.
b.) Use the initial guess $ x_{0}=1 $.
c.) Use the initial guess $ x_{0}=-1 $.
Click HERE to see a detailed solution to problem 1.
- PROBLEM 2 : Apply Newton's Method to the equation $ x^3=x^2+2 $. Begin with the given initial guess, $ x_{0} $, and find $ x_{1} $ and $ x_{2} $. Then use a spreadsheet or some other technology tool to find the solution to this equation to five decimal places.
a.) Use the initial guess $ x_{0}=1 $.
b.) Use the initial guess $ x_{0}=2 $.
c.) Use the initial guess $ x_{0}=0.5 $.
d.) Use the initial guess $ x_{0}=1000 $ !
e.) Use the initial guess $ x_{0}=-500 $ !
Click HERE to see a detailed solution to problem 2.
- PROBLEM 3 : Use Newton's Method to estimate the value of $ \ 100^{1/5} \ $ to eight decimal places.
Click HERE to see a detailed solution to problem 3.
- PROBLEM 4 : Use Newton's Method to estimate the value of $ \pi $ to ten decimal places. NOTE: There are many possible functions to use which will lead to a correct solution.
Click HERE to see a detailed solution to problem 4.
- PROBLEM 5 : Apply Newton's Method to the equation $ f(x)=0 $, where function $f$ is given below. Start with an initial guess of $ x_{0}=h>0 $.
$$ f(x) = \cases{ \sqrt{x} , \ if \ x \ge 0 \cr
-\sqrt{-x} , \ if \ x<0 \cr } $$
Click HERE to see a detailed solution to problem 5.
Click HERE to return to the original list of various types of calculus problems.
Your comments and suggestions are welcome. Please e-mail any correspondence to Duane Kouba by
clicking on the following address :
kouba@math.ucdavis.edu
A heartfelt "Thank you" goes to The MathJax Consortium for making the construction of this webpage fun and easy.
Duane Kouba ...
September 20, 2020



