SOLUTION 5: We want to solve the equation $ f(x)=0 $ for the function
$$ f(x) = \cases{ \sqrt{x} , \ if \ x \ge 0 \cr
-\sqrt{-x} , \ if \ x<0 \cr } $$
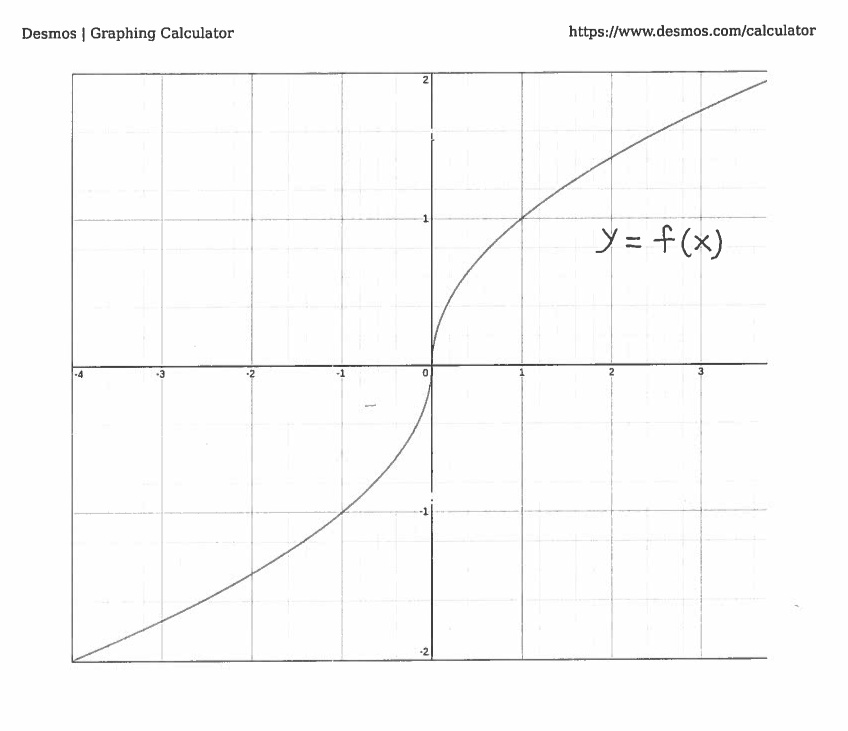
It's graph is given here.
The derivative of $f$ is
$$ f'(x) = { 1 \over 2 }x^{-1/2} = { 1 \over 2 \sqrt{x} } \ \ \ \ \ if \ \ x>0 $$
and
$$ f'(x) = { 1 \over 2 }(-x)^{-1/2}(-1) = { -1 \over 2 \sqrt{-x} } \ \ \ \ \ if \ \ x<0 $$
Now use Newton's Method. If $ x_{n}>0 $ then
$$ x_{n+1} = x_{n} - { f(x_{n}) \over f'(x_{n}) } \ \ \ \ \longrightarrow $$
$$ x_{n+1} = x_{n} - { \sqrt{x_{n}} \over { 1 \over 2 \ \sqrt{x_{n}} } } \ \ \ \ \longrightarrow $$
$$ x_{n+1} = x_{n} - 2 x_{n} \ \ \ \ \longrightarrow $$
$$ x_{n+1} = - x_{n} $$
If $ x_{n}<0 $ then
$$ x_{n+1} = x_{n} - { f(x_{n}) \over f'(x_{n}) } \ \ \ \ \longrightarrow $$
$$ x_{n+1} = x_{n} - { \sqrt{-x_{n}} \over { -1 \over 2 \ \sqrt{-x_{n}} } } \ \ \ \ \longrightarrow $$
$$ x_{n+1} = x_{n} + 2(- x_{n}) \ \ \ \ \longrightarrow $$
$$ x_{n+1} = - x_{n} $$
We can conclude that Newton's Method formula is
$$ x_{n+1} = - x_{n} $$
for any $ x_{n} \ne 0 $.
Begin with the initial guess of $ x_{0}= h>0 $. Using Newton's Method we get that
$$ x_{1} = - x_{0}= -h \ \ \ \ \longrightarrow $$
$$ x_{2} = - x_{1} = -(-h) = h \ \ \ \ \longrightarrow $$
$$ x_{3} = - x_{2} = -h \ \ \ \ \longrightarrow $$
$$ x_{4} = - x_{3} = -(-h) = h \ \ \ \ \longrightarrow $$
etc. It's clear that Newton's Method is trapped in an endless loop, which fails to converge to the solution $x=0$. This example shows that Newton's Method sometimes fails to work.
Click HERE to return to the list of problems.

