Prove that ![]() . Begin by letting
. Begin by letting ![]() be given. Find
be given. Find ![]() so that if
so that if ![]() , then
, then ![]() , i.e.,
, i.e., ![]() , i.e.,
, i.e., ![]() . But this trivial inequality is always true, no matter what value is chosen for
. But this trivial inequality is always true, no matter what value is chosen for ![]() . For example,
. For example, ![]() will work. Thus, if
will work. Thus, if ![]() , then it follows that
, then it follows that ![]() . This completes the proof.
. This completes the proof.
Click HERE to return to the list of problems.
SOLUTION 2 :
Prove that ![]() . Begin by letting
. Begin by letting ![]() be given. Find
be given. Find ![]() (which depends on
(which depends on ![]() ) so that if
) so that if ![]() , then
, then ![]() . Begin with
. Begin with ![]() and ``solve for" |x-10| . Then,
and ``solve for" |x-10| . Then,
![]() iff
iff ![]()
iff ![]()
iff ![]()
iff ![]()
iff ![]() .
.
Now choose ![]() .
Thus, if
.
Thus, if ![]() , it follows that
, it follows that ![]() . This completes the proof.
. This completes the proof.
Click HERE to return to the list of problems.
SOLUTION 3 :
Prove that ![]() . Begin by letting
. Begin by letting ![]() be given. Find
be given. Find ![]() (which depends on
(which depends on ![]() ) so that if
) so that if ![]() , then
, then ![]() . Begin with
. Begin with ![]() and ``solve for"
and ``solve for"
![]() . Then,
. Then,
![]() iff
iff ![]()
iff ![]()
iff ![]()
iff ![]()
iff ![]()
iff ![]() .
.
Now choose ![]() .
Thus, if
.
Thus, if ![]() , it follows that
, it follows that ![]() . This completes the proof.
. This completes the proof.
Click HERE to return to the list of problems.
SOLUTION 4 :
Prove that ![]() . Begin by letting
. Begin by letting ![]() be given. Find
be given. Find ![]() (which depends on
(which depends on ![]() ) so that if
) so that if ![]() , then
, then ![]() . Begin with
. Begin with ![]() and ``solve for"
|x-1| . Then,
and ``solve for"
|x-1| . Then,
![]() iff
iff ![]()
iff ![]()
iff ![]()
iff ![]() .
.
We will now ``replace" the term |x+1| with an appropriate constant and keep the term |x-1| , since this is the term we wish to ``solve for". To do this, we will arbitrarily assume that ![]() (This is a valid assumption to make since, in general, once we find a
(This is a valid assumption to make since, in general, once we find a ![]() that works, all smaller values of
that works, all smaller values of ![]() also work.) . Then
also work.) . Then ![]() implies that -1 < x-1 < 1 and 0 < x < 2 so that 1 < |x+1| < 3 (Make sure that you understand this step before proceeding.). It follows that (Always make this ``replacement" between your last expression on the left and
implies that -1 < x-1 < 1 and 0 < x < 2 so that 1 < |x+1| < 3 (Make sure that you understand this step before proceeding.). It follows that (Always make this ``replacement" between your last expression on the left and ![]() . This guarantees the logic of the proof.)
. This guarantees the logic of the proof.)
![]()
iff ![]()
iff ![]() .
.
Now choose ![]() (This guarantees that both assumptions made about
(This guarantees that both assumptions made about ![]() in the course of this proof are taken into account simultaneously.).
Thus, if
in the course of this proof are taken into account simultaneously.).
Thus, if ![]() , it follows that
, it follows that ![]() . This completes the proof.
. This completes the proof.
Click HERE to return to the list of problems.
SOLUTION 5 :
Prove that ![]() . Begin by letting
. Begin by letting ![]() be given. Find
be given. Find ![]() (which depends on
(which depends on ![]() ) so that if
) so that if ![]() , then
, then ![]() . Begin with
. Begin with ![]() and ``solve for"
| x - (-1) | = | x + 1 | . Then,
and ``solve for"
| x - (-1) | = | x + 1 | . Then,
![]() iff
iff ![]()
iff ![]()
iff ![]()
iff ![]() .
.
We will now ``replace" the term |x-1| with an appropriate constant and keep the term |x+1| , since this is the term we wish to ``solve for". To do this, we will arbitrarily assume that ![]() (This is a valid assumption to make since, in general, once we find a
(This is a valid assumption to make since, in general, once we find a ![]() that works, all smaller values of
that works, all smaller values of ![]() also work.). Then
also work.). Then ![]() implies that -1 < x+1 < 1 and -2 < x < 0 so that 1 < |x-1| < 3 (Make sure that you understand this step before proceeding.). It follows that (Always make this ``replacement" between your last expression on the left and
implies that -1 < x+1 < 1 and -2 < x < 0 so that 1 < |x-1| < 3 (Make sure that you understand this step before proceeding.). It follows that (Always make this ``replacement" between your last expression on the left and ![]() . This guarantees the logic of the proof.)
. This guarantees the logic of the proof.)
![]()
iff ![]()
iff ![]() .
.
Now choose ![]() (This guarantees that both assumptions made about
(This guarantees that both assumptions made about ![]() in the course of this proof are taken into account simultaneously.).
Thus, if
in the course of this proof are taken into account simultaneously.).
Thus, if ![]() , it follows that
, it follows that ![]() . This completes the proof.
. This completes the proof.
Click HERE to return to the list of problems.
SOLUTION 6 :
Prove that ![]() . Begin by letting
. Begin by letting ![]() be given. Find
be given. Find ![]() (which depends on
(which depends on ![]() ) so that if
) so that if ![]() , then
, then ![]() . Begin with
. Begin with ![]() and ``solve for" | x - 2 | . Then,
and ``solve for" | x - 2 | . Then,
![]() iff
iff ![]()
iff ![]()
iff ![]() .
.
We will now ``replace" the term |3x+5| with an appropriate constant and keep the term |x-2| , since this is the term we wish to ``solve for". To do this, we will arbitrarily assume that ![]() (This is a valid assumption to make since, in general, once we find a
(This is a valid assumption to make since, in general, once we find a ![]() that works, all smaller values of
that works, all smaller values of ![]() also work.) . Then
also work.) . Then ![]() implies that -1 < x-2 < 1 and 1 < x < 3 so that 8 < |3x+5| < 14 (Make sure that you understand this step before proceeding.). It follows that (Always make this ``replacement" between your last expression on the left and
implies that -1 < x-2 < 1 and 1 < x < 3 so that 8 < |3x+5| < 14 (Make sure that you understand this step before proceeding.). It follows that (Always make this ``replacement" between your last expression on the left and ![]() . This guarantees the logic of the proof.)
. This guarantees the logic of the proof.)
![]()
iff ![]()
iff ![]() .
.
Now choose ![]() (This guarantees that both assumptions made about
(This guarantees that both assumptions made about ![]() in the course of this proof are taken into account simultaneously.).
Thus, if
in the course of this proof are taken into account simultaneously.).
Thus, if ![]() , it follows that
, it follows that ![]() . This completes the proof.
. This completes the proof.
Click HERE to return to the list of problems.
SOLUTION 7 :
Prove that ![]() . Begin by letting
. Begin by letting ![]() be given. Find
be given. Find ![]() (which depends on
(which depends on ![]() ) so that if
) so that if ![]() , then
, then ![]() . Begin with
. Begin with ![]() and ``solve for" | x - 3 | . Then,
and ``solve for" | x - 3 | . Then,
![]() iff
iff ![]()
iff ![]()
iff ![]()
iff ![]()
iff ![]()
iff ![]()
iff ![]()
iff ![]() .
.
We will now ``replace" the term |x+3| with an appropriate constant and keep the term |x-3| , since this is the term we wish to ``solve for". To do this, we will arbitrarily assume that ![]() (This is a valid assumption to make since, in general, once we find a
(This is a valid assumption to make since, in general, once we find a ![]() that works, all smaller values of
that works, all smaller values of ![]() also work.) . Then
also work.) . Then ![]() implies that -1 < x-3 < 1 and 2 < x < 4 so that 5 < |x+3| < 7 and
implies that -1 < x-3 < 1 and 2 < x < 4 so that 5 < |x+3| < 7 and ![]() (Make sure that you understand this step before proceeding.). It follows that (Always make this ``replacement" between your last expression on the left and
(Make sure that you understand this step before proceeding.). It follows that (Always make this ``replacement" between your last expression on the left and ![]() . This guarantees the logic of the proof.)
. This guarantees the logic of the proof.)
![]()
iff ![]()
iff ![]()
iff ![]() .
.
Now choose ![]() (This guarantees that both assumptions made about
(This guarantees that both assumptions made about ![]() in the course of this proof are taken into account simultaneously.).
Thus, if
in the course of this proof are taken into account simultaneously.).
Thus, if ![]() , it follows that
, it follows that ![]() . This completes the proof.
. This completes the proof.
Click HERE to return to the list of problems.
SOLUTION 8 :
Prove that ![]() . Begin by letting
. Begin by letting ![]() be given. Find
be given. Find ![]() (which depends on
(which depends on ![]() ) so that if
) so that if ![]() , then
, then ![]() . Begin with
. Begin with ![]() and ``solve for" | x - (-6) | = | x + 6 | . Then,
and ``solve for" | x - (-6) | = | x + 6 | . Then,
![]() iff
iff ![]()
iff ![]()
iff ![]()
iff ![]()
iff ![]()
iff ![]()
iff ![]()
iff ![]() .
.
We will now ``replace" the term |2-x| with an appropriate constant and keep the term |x+6| , since this is the term we wish to ``solve for". To do this, we will arbitrarily assume that ![]() (This is a valid assumption to make since, in general, once we find a
(This is a valid assumption to make since, in general, once we find a ![]() that works, all smaller values of
that works, all smaller values of ![]() also work.) . Then
also work.) . Then ![]() implies that -1 < x+6 < 1 and -7 < x < -5 so that 7 < |2-x| < 9 and
implies that -1 < x+6 < 1 and -7 < x < -5 so that 7 < |2-x| < 9 and ![]() (Make sure that you understand this step before proceeding.). It follows that (Always make this ``replacement" between your last expression on the left and
(Make sure that you understand this step before proceeding.). It follows that (Always make this ``replacement" between your last expression on the left and ![]() . This guarantees the logic of the proof.)
. This guarantees the logic of the proof.)
![]() .
.
iff ![]() .
.
iff ![]()
iff ![]() .
.
Now choose ![]() (This guarantees that both assumptions made about
(This guarantees that both assumptions made about ![]() in the course of this proof are taken into account simultaneously.).
Thus, if
in the course of this proof are taken into account simultaneously.).
Thus, if ![]() , it follows that
, it follows that ![]() . This completes the proof.
. This completes the proof.
Click HERE to return to the list of problems.
SOLUTION 9 :
Prove that ![]() .
Begin by letting
.
Begin by letting ![]() be given. Find
be given. Find ![]() (which depends on
(which depends on ![]() ) so that if
) so that if ![]() , then
, then ![]() . Begin with
. Begin with ![]() and ``solve for" | x - 3 | . Then,
and ``solve for" | x - 3 | . Then,
![]() iff
iff ![]()
iff ![]()
iff ![]()
iff ![]()
iff ![]()
iff ![]()
iff ![]() .
.
We will now ``replace" the term | 4x-9 | with an appropriate constant and keep the term |x-3| , since this is the term we wish to ``solve for". To do this, we will arbitrarily assume that ![]() (This is a valid assumption to make since, in general, once we find a
(This is a valid assumption to make since, in general, once we find a ![]() that works, all smaller values of
that works, all smaller values of ![]() also work.) . Then
also work.) . Then ![]() implies that -1 < x-3 < 1 and 2 < x < 4 . HOWEVER, THIS RANGE OF X-VALUES IS NOT APPROPRIATE SINCE THE FUNCTION
implies that -1 < x-3 < 1 and 2 < x < 4 . HOWEVER, THIS RANGE OF X-VALUES IS NOT APPROPRIATE SINCE THE FUNCTION ![]() IS NOT DEFINED AT
IS NOT DEFINED AT ![]() ! Fortunately, this problem can be easily resolved. We simply pick
! Fortunately, this problem can be easily resolved. We simply pick ![]() small enough to avoid
small enough to avoid ![]() . For example, assume that
. For example, assume that ![]() . Then
. Then ![]() implies that
implies that ![]() and
and ![]() so that 2 < | 4x-9 | < 4 and
so that 2 < | 4x-9 | < 4 and ![]() (Make sure that you understand this step before proceeding.). It follows that (Always make this ``replacement" between your last expression on the left and
(Make sure that you understand this step before proceeding.). It follows that (Always make this ``replacement" between your last expression on the left and ![]() . This guarantees the logic of the proof.)
. This guarantees the logic of the proof.)
![]() .
.
iff ![]()
iff ![]()
iff ![]() .
.
Now choose ![]() (This guarantees that both assumptions made about
(This guarantees that both assumptions made about ![]() in the course of this proof are taken into account simultaneously.).
Thus, if
in the course of this proof are taken into account simultaneously.).
Thus, if ![]() , it follows that
, it follows that ![]() . This completes the proof.
. This completes the proof.
Click HERE to return to the list of problems.
SOLUTION 10 :
Prove that ![]() .
Begin by letting
.
Begin by letting ![]() be given. Find
be given. Find ![]() (which depends on
(which depends on ![]() ) so that if
) so that if ![]() , then
, then ![]() . Begin with
. Begin with ![]() and ``solve for" | x - 9 | . Then,
and ``solve for" | x - 9 | . Then,
![]() iff
iff ![]()
iff ![]()
(At this point, we need to figure out a way to make | x-9 | ``appear'' in our computations. Appropriate use of the conjugate will suffice.)
iff ![]()
(Recall that ![]() .)
.)
iff ![]()
iff ![]() .
.
iff ![]() .
.
We will now ``replace" the term ![]() with an appropriate constant and keep the term |x-9| , since this is the term we wish to ``solve for". To do this, we will arbitrarily assume that
with an appropriate constant and keep the term |x-9| , since this is the term we wish to ``solve for". To do this, we will arbitrarily assume that ![]() (This is a valid assumption to make since, in general, once we find a
(This is a valid assumption to make since, in general, once we find a ![]() that works, all smaller values of
that works, all smaller values of ![]() also work.) . Then
also work.) . Then ![]() implies that -1 < x-9 < 1 and 8 < x < 10 so that
implies that -1 < x-9 < 1 and 8 < x < 10 so that ![]() and
and ![]() (Make sure that you understand this step before proceeding.). It follows that (Always make this ``replacement" between your last expression on the left and
(Make sure that you understand this step before proceeding.). It follows that (Always make this ``replacement" between your last expression on the left and ![]() . This guarantees the logic of the proof.)
. This guarantees the logic of the proof.)
![]()
iff ![]()
iff ![]() .
.
Now choose ![]() (This guarantees that both assumptions made about
(This guarantees that both assumptions made about ![]() in the course of this proof are taken into account simultaneously.).
Thus, if
in the course of this proof are taken into account simultaneously.).
Thus, if ![]() , it follows that
, it follows that ![]() . This completes the proof.
. This completes the proof.
Click HERE to return to the list of problems.
SOLUTION 11 :
Prove that ![]() .
Begin by letting
.
Begin by letting ![]() be given. Find
be given. Find ![]() (which depends on
(which depends on ![]() ) so that if
) so that if ![]() , then
, then ![]() . Begin with
. Begin with ![]() and ``solve for" | x - 4 | . Then,
and ``solve for" | x - 4 | . Then,
![]() iff
iff ![]()
(At this point, we need to figure out a way to make | x-4 | ``appear'' in our computations. Appropriate use of the conjugate will suffice.)
iff ![]()
(Recall that ![]() .)
.)
iff ![]()
iff ![]()
iff ![]()
iff ![]() .
.
We will now ``replace" the term ![]() with an appropriate constant and keep the term |x-4| , since this is the term we wish to ``solve for". To do this, we will arbitrarily assume that
with an appropriate constant and keep the term |x-4| , since this is the term we wish to ``solve for". To do this, we will arbitrarily assume that ![]() (This is a valid assumption to make since, in general, once we find a
(This is a valid assumption to make since, in general, once we find a ![]() that works, all smaller values of
that works, all smaller values of ![]() also work.) . Then
also work.) . Then ![]() implies that -1 < x-4 < 1 and 3 < x < 5 so that
implies that -1 < x-4 < 1 and 3 < x < 5 so that ![]() and
and ![]() (Make sure that you understand this step before proceeding.). It follows that (Always make this ``replacement" between your last expression on the left and
(Make sure that you understand this step before proceeding.). It follows that (Always make this ``replacement" between your last expression on the left and ![]() . This guarantees the logic of the proof.)
. This guarantees the logic of the proof.)
![]()
iff ![]()
iff ![]() .
.
Now choose ![]() (This guarantees that both assumptions made about
(This guarantees that both assumptions made about ![]() in the course of this proof are taken into account simultaneously.).
Thus, if
in the course of this proof are taken into account simultaneously.).
Thus, if ![]() , it follows that
, it follows that ![]() . This completes the proof.
. This completes the proof.
Click HERE to return to the list of problems.
SOLUTION 12 :
Prove that ![]() . Begin by letting
. Begin by letting ![]() be given. Find
be given. Find ![]() (which depends on
(which depends on ![]() ) so that if
) so that if ![]() , then
, then ![]() . Begin with
. Begin with ![]() and ``solve for" | x - 1 | . Then,
and ``solve for" | x - 1 | . Then,
![]() iff
iff ![]()
iff ![]()
iff ![]()
iff ![]()
iff ![]()
(At this point, we need to figure out a way to make | x-1 | ``appear'' in our computations. A simple use of constants will get us started.)
iff ![]()
iff ![]()
iff ![]()
(We need to be able to factor (x-1) from the numerator. Apply the conjugate to the term ![]() .)
.)
iff ![]()
iff ![]()
iff ![]()
iff ![]()
(Now get a common denominator.)
iff ![]()
iff ![]()
iff ![]()
iff ![]()
iff ![]() .
.
We will now ``replace" the terms ![]() and
and ![]() with appropriate constants and keep the term |x-1| , since this is the term we wish to ``solve for". To do this, we will arbitrarily assume that
with appropriate constants and keep the term |x-1| , since this is the term we wish to ``solve for". To do this, we will arbitrarily assume that ![]() (This is a valid assumption to make since, in general, once we find a
(This is a valid assumption to make since, in general, once we find a ![]() that works, all smaller values of
that works, all smaller values of ![]() also work.). Then
also work.). Then ![]() implies that -1 < x-1 < 1 and 0 < x < 2 so that
implies that -1 < x-1 < 1 and 0 < x < 2 so that ![]() . In addition,
. In addition, ![]() so that
so that ![]() and
and
![]() (Make sure that you understand these steps before proceeding.). It follows that (Always make this ``replacement" between your last expression on the left and
(Make sure that you understand these steps before proceeding.). It follows that (Always make this ``replacement" between your last expression on the left and ![]() . This guarantees the logic of the proof.)
. This guarantees the logic of the proof.)
![]()
iff ![]()
iff ![]() .
.
Now choose ![]() (This guarantees that both assumptions made about
(This guarantees that both assumptions made about ![]() in the course of this proof are taken into account simultaneously.).
Thus, if
in the course of this proof are taken into account simultaneously.).
Thus, if ![]() , it follows that
, it follows that ![]() . This completes the proof.
. This completes the proof.
Click HERE to return to the list of problems.
SOLUTION 13 :
Prove that ![]() . Begin by letting
. Begin by letting ![]() be given. Find
be given. Find ![]() (which depends on
(which depends on ![]() ) so that if
) so that if ![]() , then
, then ![]() . Begin with
. Begin with ![]() and ``solve for" | x - a | . Then,
and ``solve for" | x - a | . Then,
![]() iff
iff ![]() .
.
At this point, we need to figure out a way to introduce the term | x-a | into our computations. The answer lies with the Mean Value Theorem. Consider the function ![]() on the interval [A, B] . Since f is continuous on the closed interval [A, B] and differentiable (
on the interval [A, B] . Since f is continuous on the closed interval [A, B] and differentiable ( ![]() ) on the open interval (A, B) , according to the Mean Value Theorem there is at least one number C , A < C < B , satisfying
) on the open interval (A, B) , according to the Mean Value Theorem there is at least one number C , A < C < B , satisfying
![]() ,
,
i.e.,
![]() .
.
Then
![]()
so that
![]() .
.
This is true for any two real numbers, A and B . It follows that (Always make this ``replacement" between your last expression on the left and ![]() . This guarantees the logic of the proof.)
. This guarantees the logic of the proof.)
![]() .
.
Now choose ![]() . Thus, if
. Thus, if ![]() , it follows that
, it follows that ![]() . This completes the proof.
. This completes the proof.
Click HERE to return to the list of problems.
SOLUTION 14 :
Prove that ![]() . Begin by letting
. Begin by letting ![]() be given. Find
be given. Find ![]() (which depends on
(which depends on ![]() ) so that if
) so that if ![]() , then
, then ![]() . Begin with
. Begin with ![]() and ``solve for" | x - a | . Then,
and ``solve for" | x - a | . Then,
![]() iff
iff ![]() .
.
At this point, we need to figure out a way to introduce the term | x-a | into our computations. The answer lies with the Mean Value Theorem. Consider the function ![]() on the interval [A, B] , where A and B are both positive. Since f is continuous on the closed interval [A, B] and differentiable (
on the interval [A, B] , where A and B are both positive. Since f is continuous on the closed interval [A, B] and differentiable ( ![]() ) on the open interval (A, B) , according to the Mean Value Theorem there is at least one number C , A < C < B , satisfying
) on the open interval (A, B) , according to the Mean Value Theorem there is at least one number C , A < C < B , satisfying
![]() ,
,
i.e.,
![]() .
.
Then, since 0 < A < C < B , it follows that
![]() , so that
, so that
![]() .
.
Thus,
(*) ![]() .
.
This is true for any two positive real numbers A and B , where B > A . At this point, we need to consider two cases.
If x > a , it follows from inequality (*) that (Always make this ``replacement" between your last expression on the left and ![]() . This guarantees the logic of the proof.)
. This guarantees the logic of the proof.)
![]()
iff ![]()
iff ![]() .
.
Now choose ![]() . Thus, if
. Thus, if ![]() , it follows that
, it follows that ![]() .
.
If x < a , then it is reasonable to assume that ![]() since we are considering the limit as x approaches a . Thus,
since we are considering the limit as x approaches a . Thus, ![]() and it follows from inequality (*) that
and it follows from inequality (*) that
![]()
so that
![]()
iff ![]()
iff ![]() .
.
Now choose ![]() . Thus, if
. Thus, if ![]() , it follows that
, it follows that ![]() . This completes the proof.
. This completes the proof.
Click HERE to return to the list of problems.
SOLUTION 15 :
Let ![]() .
Prove that
.
Prove that ![]() does not exist .
does not exist .
ASSUME THAT THE LIMIT DOES EXIST. That is, assume that
![]() , where L is some real number. It follows that for EACH real number
, where L is some real number. It follows that for EACH real number ![]() , there exists another real number
, there exists another real number ![]() so that
so that
if ![]() , then
, then ![]() .
.
We will proceed to find ONE ![]() for which NO
for which NO ![]() works. THIS WILL BE A CONTRADICTION OF OUR ASSUMPTION, making our assumption false, proving that the limit does not exist. (This method is called proof by contradiction.)
works. THIS WILL BE A CONTRADICTION OF OUR ASSUMPTION, making our assumption false, proving that the limit does not exist. (This method is called proof by contradiction.)
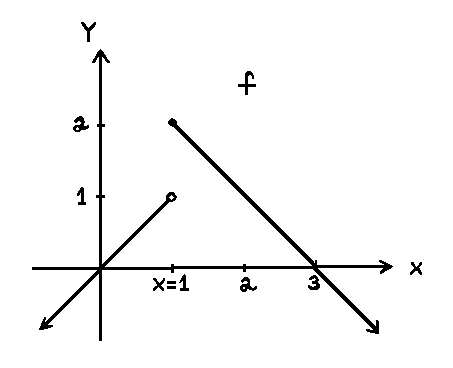
By looking at the graph of f , which is given above, we see that x-values chosen ``near'' to x=1 but on opposite sides of x=1 have corresponding y-values which are ``about'' one unit apart. Intuitively, this tells us that the limit does not exist and leads us to choose an appropriate ![]() leading to the above contradiction.
leading to the above contradiction.
Consider ![]() . Under our assumption that the limit does exist, it follows that there is some number
. Under our assumption that the limit does exist, it follows that there is some number ![]() so that if
so that if ![]() , then
, then ![]() . But for ANY choice of
. But for ANY choice of ![]()
![]() iff
iff ![]() (and x not equal to 1)
(and x not equal to 1)
iff ![]() (and x not equal to 1) .
(and x not equal to 1) .
Thus, both ![]() and
and ![]() satisfy
satisfy ![]() , which implies that
, which implies that
![]() and
and ![]() .
.
In addition,
![]()
![]()
![]()
![]()
= | -1 |
= 1 .
Now, by the triangle inequality
![]()
![]()
![]()
![]()
![]()
= 1 .
We have just concluded that
![]() ,
,
an obvious contradiction. It must be that the original limit does not exist.
Click HERE to return to the list of problems.