Then
![]()
![]()
![]() .
.
Click HERE to return to the list of problems.
SOLUTION 2 : Differentiate ![]() .
.
Then
![]()
![]()
![]()
![]()
![]() .
.
Click HERE to return to the list of problems.
SOLUTION 3 : Differentiate ![]() .
.
Then
![]()
![]()
![]()
![]()
![]() .
.
Click HERE to return to the list of problems.
SOLUTION 4 : Differentiate ![]() .
.
Then
![]()
![]()
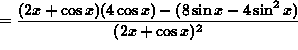
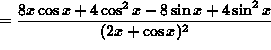
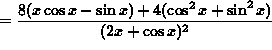
(Recall the well-known trigonometry identity ![]() .)
.)
![]()
![]() .
.
Click HERE to return to the list of problems.
SOLUTION 5 : Differentiate ![]() .
.
Then
![]()
![]()
![]()
![]()
![]()
![]() .
.
Click HERE to return to the list of problems.
SOLUTION 6 : Differentiate ![]() .
.
Then
![]()
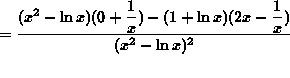
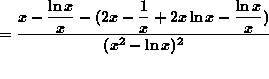
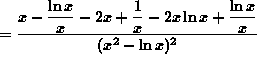
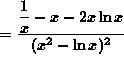
(Begin to simplify the final answer by getting a common denominator in the numerator.)
![]()
![]()
![]() .
.
Click HERE to return to the list of problems.
SOLUTION 7 : Differentiate ![]() .
.
Then
![]()
(Recall that ![]() .)
.)
![]()
![]()
(Recall that ![]() and
and ![]() .)
.)
![]()
![]()
![]()
(Recall that ![]() .)
.)
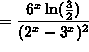 .
.
Click HERE to return to the list of problems.
SOLUTION 8 : Differentiate ![]() .
.
Then
![]()
![]()
![]()
(Factor 2x and ![]() from the numerator.)
from the numerator.)
![]()
![]()
![]()
![]()
![]() .
.
Click HERE to return to the list of problems.
SOLUTION 9 : Consider the function ![]() . Evaluate
. Evaluate ![]() .
Use the quotient rule to find the derivative of f . Then
.
Use the quotient rule to find the derivative of f . Then
![]()
(Recall that ![]() and
and ![]() .)
.)
![]()
![]()
![]()
(Factor ![]() from the numerator.)
from the numerator.)
![]()
![]() .
.
Finally,
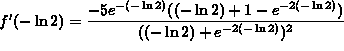
![]()
(Recall that ![]() and
and ![]() .)
.)
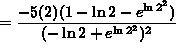
![]()
![]()
![]() .
.
Click HERE to return to the list of problems.
SOLUTION 10 : Differentiate ![]() . Apply
the quotient rule first. Then
. Apply
the quotient rule first. Then
![]()
(Apply the product rule in the first part of the numerator.)
![]()
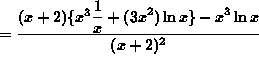
![]()
(Factor ![]() from inside the brackets.)
from inside the brackets.)
![]()
(Now factor ![]() from the numerator.)
from the numerator.)
![]()
![]()
![]() .
.
Click HERE to return to the list of problems.
SOLUTION 11 : Differentiate ![]() . Apply the quotient rule first. Then
. Apply the quotient rule first. Then
![]()
(Now apply the product rule in the first part of the numerator.)
![]()
![]()
![]()
(Factor 2x and ![]() from inside the brackets.)
from inside the brackets.)
![]()
(Factor ![]() , and
, and ![]() from the numerator.)
from the numerator.)
![]()
![]()
![]()
![]() .
.
Click HERE to return to the list of problems.