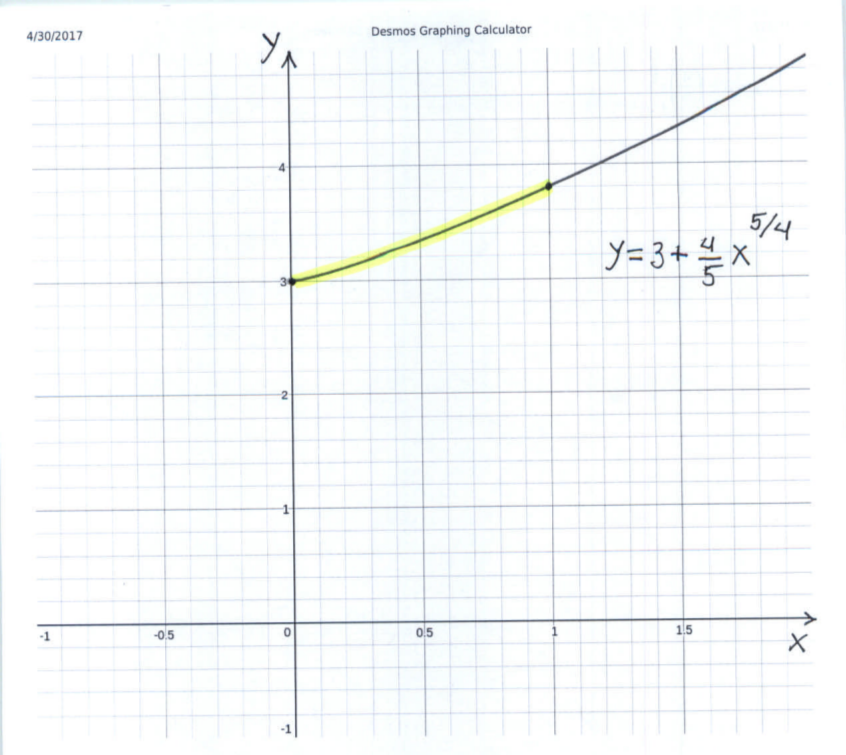
SOLUTION 4: $ \ \ $ If $ y = 3 + (4/5)x^{5/4} $ for $ 0 \le x \le 1 $, then $ \displaystyle{ { dy \over dx} = (4/5)(5/4)x^{1/4}=x^{1/4} } $
so that
$$ ARC = \displaystyle{ \int_{0}^{1} \sqrt{ 1 + \Big({dy \over dx}\Big)^2 } \ dx } $$
$$ = \displaystyle{ \int_{0}^{1} \sqrt{ 1 + (x^{1/4})^2 } \ dx } $$
$$ = \displaystyle{ \int_{0}^{1} \sqrt{ 1 + x^{1/2} } \ dx } $$
$$ = \displaystyle{ \int_{0}^{1} \sqrt{ 1 + \sqrt{x} } \ dx } $$
(Now integrate using the method of "power" u-substitution. Let $ u= \sqrt{1 + \sqrt{x}} \ \longrightarrow $
$ u^2 = 1 + \sqrt{x} \ \longrightarrow \ \sqrt{x} = u^2-1 \ \longrightarrow \ x = (u^2-1)^2 = u^4 -2u^2+1 \ \longrightarrow \ $
$ dx = (4u^3-4u) du \ $ .)
$$ = \displaystyle{ \int_{x=0}^{x=1} \sqrt{ u^2 } (4u^3-4u) \ du } $$
$$ = \displaystyle{ \int_{x=0}^{x=1} u (4u^3-4u) \ du } $$
$$ = \displaystyle{ \int_{x=0}^{x=1} (4u^4-4u^2) \ du } $$
$$ = \displaystyle{ ( (4/5)u^5-(4/3)u^3) \ \Big\vert_{x=0}^{x=1} } $$
$$ = \displaystyle{ \Big( (4/5) \Big(\sqrt{ 1 + \sqrt{x} } \Big)^5-(4/3) \Big(\sqrt{ 1 + \sqrt{x} } \Big)^3 \Big) \ \Big\vert_{0}^{1} } $$
$$ = \displaystyle{ \Big( (4/5) \Big(\sqrt{ 1 + \sqrt{1} } \Big)^5-(4/3) \Big(\sqrt{ 1 + \sqrt{1} } \Big)^3 \Big) }
- \displaystyle{ \Big( (4/5) \Big(\sqrt{ 1 + \sqrt{0} } \Big)^5-(4/3) \Big(\sqrt{ 1 + \sqrt{0} } \Big)^3 \Big) } $$
$$ = \displaystyle{ \Big( (4/5) \Big(\sqrt{ 2 } \Big)^5-(4/3) \Big(\sqrt{ 2 } \Big)^3 \Big) }
- \displaystyle{ \Big( (4/5) \Big(\sqrt{ 1 } \Big)^5-(4/3) \Big(\sqrt{ 1 } \Big)^3 \Big) } $$
$$ = \displaystyle{4 \over 5}(4 \sqrt{2}) - \displaystyle{4 \over 3}(2 \sqrt{2}) - \Big(\displaystyle{12 \over 15} - \displaystyle{20 \over 15} \Big) $$
$$ = \Big( \displaystyle{{16 \over 5} - {8 \over 3}} \Big) \sqrt{2} + \displaystyle{8 \over 15} $$
$$ = \Big( \displaystyle{{48 \over 15} - {40 \over 15}} \Big) \sqrt{2} + \displaystyle{8 \over 15} $$
$$ = \displaystyle{8 \over 15} \sqrt{2} + \displaystyle{8 \over 15} $$
$$ = \displaystyle{8 \over 15} ( \sqrt{2} + 1) $$
Click HERE to return to the list of problems.

