COMPUTING THE ARC LENGTH OF A DIFFERENTIABLE FUNCTION ON A CLOSED INTERVAL
The following problems involve the computation of arc length of differentiable functions on closed intervals. Let's first begin by finding a general formula for computing arc length. Consider a graph of a function of unknown length $L$ which can be represented as $ y=f(x) $ for $ a \le x \le b $ or $ x=g(y) $ for $ c \le y \le d $. We will derive the arc length formula using the differential of arc length, $ ds $, a small change in arc length $s$, and write $ds$ in terms of $dx$, the differential of $x$, and $dy$, the differential of $y$ (See the graph below.).
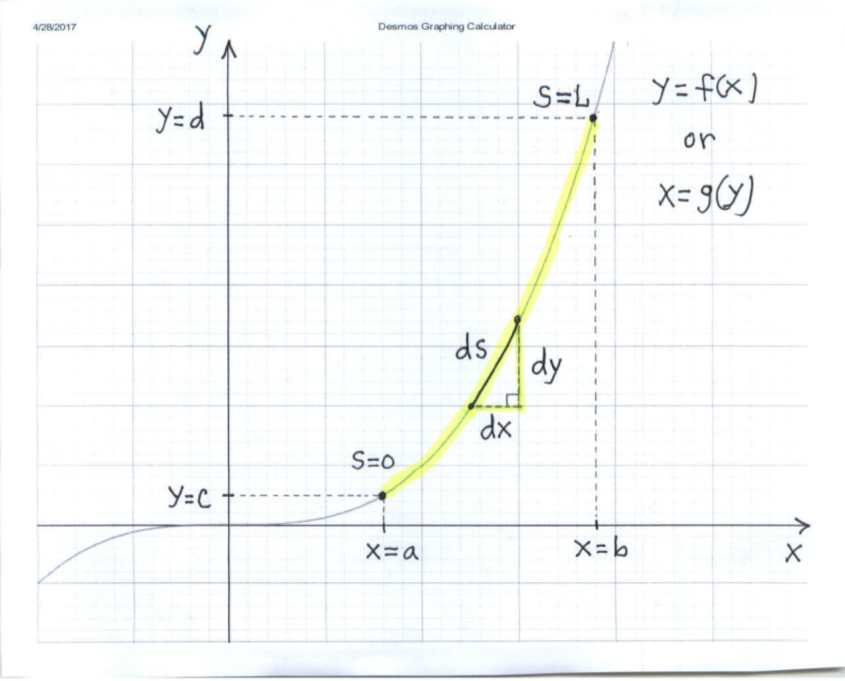
Using the Pythagorean Theorem we will assume that
$$ (ds)^2 = (dx)^2 + (dy)^2 $$
so that
$$ ds = \sqrt{ (dx)^2 + (dy)^2 } $$
It then follows that the total arc length $L$ from $x=a$ to $x=b$ is
$$ ARC = \displaystyle{ \int_{s=0}^{s=L} 1 \ ds } = \displaystyle{ \int_{x=a}^{x=b} \sqrt{ (dx)^2 + (dy)^2 } } $$
$$ = \displaystyle{ \int_{a}^{b} \sqrt{ \Bigg(1 + {(dy)^2 \over (dx)^2}\Bigg) (dx)^2} } $$
$$ = \displaystyle{ \int_{a}^{b} \sqrt{ 1 + \Big({dy \over dx}\Big)^2 } dx } $$
i.e.,
$$ ARC = \displaystyle{ \int_{a}^{b} \sqrt{ 1 + \Big({dy \over dx}\Big)^2 } dx } $$
Similarly, it follows that the total arc length $L$ from $y=c$ to $y=d$ is
$$ ARC = \displaystyle{ \int_{s=0}^{s=L} 1 \ ds } = \displaystyle{ \int_{y=c}^{y=d} \sqrt{ (dx)^2 + (dy)^2 } } $$
$$ = \displaystyle{ \int_{c}^{d} \sqrt{ \Bigg({(dx)^2 \over (dy)^2} + 1 \Bigg) (dy)^2} } $$
$$ = \displaystyle{ \int_{c}^{d} \sqrt{ 1 + \Big({dx \over dy}\Big)^2 } dy } $$
i.e.,
$$ ARC = \displaystyle{ \int_{c}^{d} \sqrt{ 1 + \Big({dx \over dy}\Big)^2 } dy } $$
Most of the following problems are average. But because the arc length formula includes a square root, most problems will require relatively intense and very careful algebraic simplification, including manipulation of fractions and creation of perfect squares.
Compute the area of the region enclosed by the graphs of the given equations. Use vertical cross-sections on Problems 1-16.
- PROBLEM 1 : Find the length of the graph for $ y = 3x+2 $ on the closed interval $ -1 \le x \le 2 $ .
Click HERE to see a detailed solution to problem 1.
- PROBLEM 2 : Find the length of the graph for $ y = x^{3/2} $ on the closed interval $ 0 \le x \le 4 $
Click HERE to see a detailed solution to problem 2.
- PROBLEM 3 : Find the length of the graph for $ y = (3/2)x^{2/3} $ on the closed interval $ 0 \le x \le 1 $ .
Click HERE to see a detailed solution to problem 3.
- PROBLEM 4 : Find the length of the graph for $ y = 3 + (4/5)x^{5/4} $ on the closed interval $ 0 \le x \le 1 $ .
Click HERE to see a detailed solution to problem 4.
- PROBLEM 5 : Find the length of the graph for $ y= \displaystyle{ { x^4 \over 4 } + { 1 \over 8x^2 } } $ on the closed interval $ 2 \le x \le 4 $ .
Click HERE to see a detailed solution to problem 5.
- PROBLEM 6 : Find the length of the graph for $ y= \displaystyle{ { x^3 \over 6 } + { 1 \over 2x } } $ on the closed interval $ 1 \le x \le 3 $ .
Click HERE to see a detailed solution to problem 6.
- PROBLEM 7 : Find the length of the graph for $ y = (1/2)(e^x + e^{-x}) $ on the closed interval $ 0 \le x \le \ln 2 $ .
Click HERE to see a detailed solution to problem 7.
- PROBLEM 8 : Find the length of the graph for $ y = (2/3)(x^2+1)^{3/2} $ on the closed interval $ 0 \le x \le 2 $ .
Click HERE to see a detailed solution to problem 8.
- PROBLEM 9 : Find the length of the graph for $ y = \displaystyle{ \ln(\cos x) } $ on the closed interval $ 0 \le x \le \pi/3 $ .
Click HERE to see a detailed solution to problem 9.
- PROBLEM 10 : Find the length of the graph for $ x = \displaystyle{ { y^4 \over 8 } + { 1 \over 4y^2 } } $ on the closed interval $ 1 \le y \le 2 $ .
Click HERE to see a detailed solution to problem 10.
- PROBLEM 11 : Find the length of the graph for $ x = \displaystyle{ { y^5 \over 5 } + { 1 \over 12y^3 } } $ on the closed interval $ 1/2 \le y \le 1 $ .
Click HERE to see a detailed solution to problem 11.
- PROBLEM 12 : Find the length of the graph for $ x = \ln y - \displaystyle{ y^2 \over 8 } $ on the closed interval $ 1 \le y \le 2 $ .
Click HERE to see a detailed solution to problem 12.
Click HERE to return to the original list of various types of calculus problems.
Your comments and suggestions are welcome. Please e-mail any correspondence to Duane Kouba by
clicking on the following address :
kouba@math.ucdavis.edu
A heartfelt "Thank you" goes to The MathJax Consortium and the online Desmos Grapher for making the construction of graphs and this webpage fun and easy.
Duane Kouba ...
May 3, 2017

